基于无线传感器网络的MCKP-MMF算法matlab仿真

最新推荐文章于 2025-05-07 09:27:15 发布

软件算法开发

最新推荐文章于 2025-05-07 09:27:15 发布

阅读量325

点赞数 2

分类专栏： MATLAB程序开发 # 网络仿真文章标签： matlab 开发语言网络

本文链接：https://blog.youkuaiyun.com/soft_algorithm/article/details/134353503

版权

MATLAB程序开发同时被 2 个专栏收录

192 篇文章

订阅专栏

网络仿真

28 篇文章

订阅专栏

本文详细阐述了MCKP-MMF算法，一种通过局部策略寻优的流量管理和资源分配算法，涉及其工作原理、核心程序段和MATLAB测试，展示了如何处理拥塞节点和半径调整以达到公平性和效率最大化。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.程序功能描述

基于流量估计，MCKP-MMF算法便可以找到本地MCKP-MMF的近似解。其基本思想与MMKP-MMF相似，但是相比之下，MCKP-MMF采取了更为简单的策略从而使之成为一种启发式算法并且运行更快。算法从最小配置开始，并将所有访问点初始化为活动状态。此后，算法在执行的每一轮中发现一个较好的部分解，并将相关的访问点置为停止状态，直至所有访问点都成为停止状态，算法终止。

某个访问点可能先后收到来自多个拥塞节点的重新设置影响半径的要求，此时为了满足带宽消耗最大的节点的带宽限制，访问点需要将其新影响半径设置为其中最小的一个。一种简单的方法是每次收到这样的请求之后，将其中包含的新影响半径与访问点当前影响半径比较，如果新影响半径较小则修改当前影响半径为新影响半径，否则访问点保持当前影响半径。这样作的一个副作用是访问点的影响半径将随时间增长而变小。从另一方面，节点由于仅通过本地信息为与之相关的访问点确定影响半径，可能无法得到访问点真正的最优影响半径。为了消除这个副作用并帮助访问点跳出本地最优状态从而更接近全局最优配置，每个访问点需要周期性的增加其影响半径。

2.测试软件版本以及运行结果展示

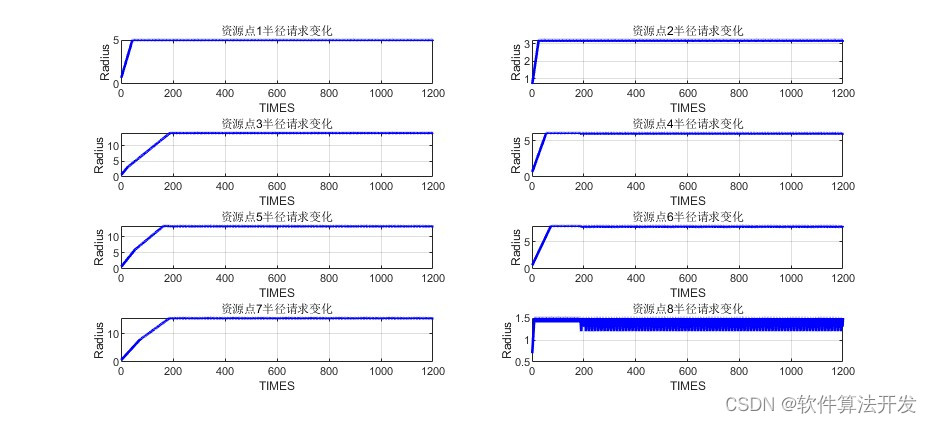
MATLAB2022a版本运行

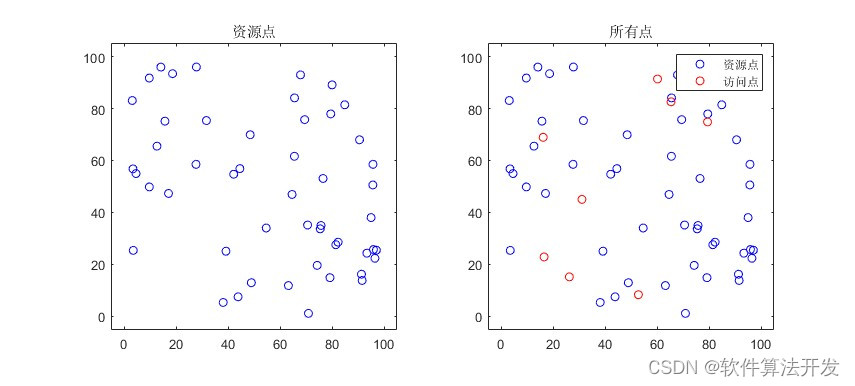
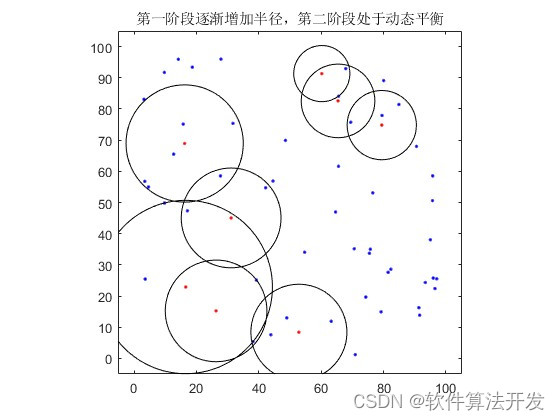
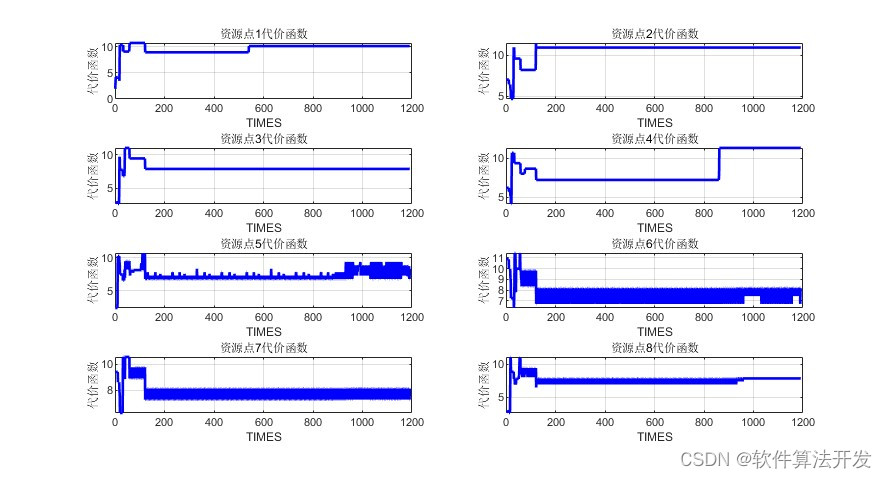
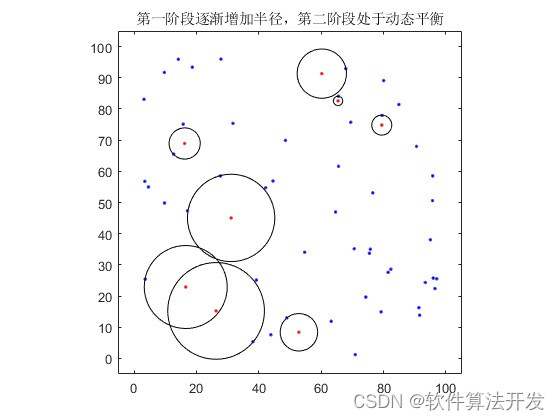
3.核心程序

..............................................................................
while(times < Stimes)
     figure(2);
     plot(Xn,Yn,'b.');
     hold on;
     plot(Xm,Ym,'r.');
     hold on;    
     
     times
     times    = times + 1;
     SATVs    = SATV*ones(1,N);
     Tpk      = zeros(M,1);    %代价函数
     NEXT_ptr = 0;
     NEXT_Set = ones(1,M);

     while(NEXT_ptr <= M)
         %所有活动访问点半径均被增加且所得为合适解
         %计算代价函数
         for j = 1:M
             for i1 = 1:N 
                 d = sqrt( (Xn(i1) - Xm(j))^2 + (Yn(i1) - Ym(j))^2 );
                 %判断是否在一定范围之内
                 if d <= Rs(j)
                    %进行资源分配
                    Tpk(j) = Tpk(j) + Requst(j,i1);
                 else
                    Tpk(j) = Tpk(j); 
                 end
             end   
         end
 
         [A,I]             = sort(Tpk);
         
         if A > 0
            %选择最小的一个
            Tpk_min           = A(1);
            Tpk_ind           = I(1);
            NEXT_Set(Tpk_ind) = 0;
            if feasible(A,rij) == 1
               %没有被违反
               Rs(Tpk_ind) = Rs(Tpk_ind) + Step;
               if (NEXT_Set(Tpk_ind)) == 0
                  NEXT_ptr = NEXT_ptr; 
               else
                  NEXT_ptr = NEXT_ptr + 1; 
               end
            else
               %违反了，则直接退出进入下一个循环
               NEXT_ptr = M+1;   
            end
         else
            %如果流量为0，则说明没有发生任何请求，其实半径自动递增
            Tpk_min     = A(1);
            Tpk_ind     = I(1); 
            Rs(Tpk_ind) = Rs(Tpk_ind) + Step;
         end 
     end
     
     %多个拥塞节点的重新设置影响半径
     for j = 1:M
         %表示该访问点处于第1阶段
         if FLag(j) == 0
            %计算每个节点到访问点的距离
            for i1 = 1:N 
                d = sqrt( (Xn(i1) - Xm(j))^2 + (Yn(i1) - Ym(j))^2 );
                %判断是否在一定范围之内
                if d <= Rs(j)
                   %进行资源分配
                   SATVs(1,i1) = SATVs(1,i1) - Requst(j,i1);
                else
                   SATVs(1,i1) = SATVs(1,i1); 
                end    
                %每次请求完之后，判断是否拥堵
                if SATVs(1,i1) <= 0%表示拥堵
                   saturated_state{j,i1} = [1,Rs',Xm(j),Ym(j),Xn(i1),Yn(i1)]; 
                   FLag(j) = 1;
                else
                   saturated_state{j,i1} = [0,zeros(1,M),0,0,0,0];  
                   FLag(j) = FLag(j);
                end
            end 
         end
%********************************************************************    
end


%绘制仿真结果
figure(3);
subplot(421);
plot(R(1,:),'b','linewidth',2);
xlabel('TIMES');
ylabel('Radius');
grid on;
title('资源点1半径请求变化');

subplot(422);
plot(R(2,:),'b','linewidth',2);
xlabel('TIMES');
ylabel('Radius');
grid on;
title('资源点2半径请求变化');

subplot(423);
plot(R(3,:),'b','linewidth',2);
xlabel('TIMES');
ylabel('Radius');
grid on;
title('资源点3半径请求变化');

subplot(424);
plot(R(4,:),'b','linewidth',2);
xlabel('TIMES');
ylabel('Radius');
grid on;
title('资源点4半径请求变化');

subplot(425);
plot(R(5,:),'b','linewidth',2);
xlabel('TIMES');
ylabel('Radius');
grid on;
title('资源点5半径请求变化');

subplot(426);
plot(R(6,:),'b','linewidth',2);
xlabel('TIMES');
ylabel('Radius');
grid on;
title('资源点6半径请求变化');

subplot(427);
plot(R(7,:),'b','linewidth',2);
xlabel('TIMES');
ylabel('Radius');
grid on;
title('资源点7半径请求变化');

subplot(428);
plot(R(8,:),'b','linewidth',2);
xlabel('TIMES');
ylabel('Radius');
grid on;
title('资源点8半径请求变化');





%绘制仿真结果
figure(4);
subplot(421);
plot(TPK(1,10:end),'b','linewidth',2);
xlabel('TIMES');
ylabel('代价函数');
grid on;
title('资源点1代价函数');

subplot(422);
plot(TPK(2,10:end),'b','linewidth',2);
xlabel('TIMES');
ylabel('代价函数');
grid on;
title('资源点2代价函数');

subplot(423);
plot(TPK(3,10:end),'b','linewidth',2);
xlabel('TIMES');
ylabel('代价函数');
grid on;
title('资源点3代价函数');

subplot(424);
plot(TPK(4,10:end),'b','linewidth',2);
xlabel('TIMES');
ylabel('代价函数');
grid on;
title('资源点4代价函数');

subplot(425);
plot(TPK(5,10:end),'b','linewidth',2);
xlabel('TIMES');
ylabel('代价函数');
grid on;
title('资源点5代价函数');

subplot(426);
plot(TPK(6,10:end),'b','linewidth',2);
xlabel('TIMES');
ylabel('代价函数');
grid on;
title('资源点6代价函数');

subplot(427);
plot(TPK(7,10:end),'b','linewidth',2);
xlabel('TIMES');
ylabel('代价函数');
grid on;
title('资源点7代价函数');

subplot(428);
plot(TPK(8,10:end),'b','linewidth',2);
xlabel('TIMES');
ylabel('代价函数');
grid on;
title('资源点8代价函数');
12_008m

4.本算法原理

算法的执行可以分为两个阶段。第一阶段是通常所谓的慢启动阶段，在该阶段，各个sink开始于最小半径的请求，然后以某种速度增加其请求半径，直到算法发现一个潜在的瓶颈节点，此时相关sink将收到<saturated>消息。算法中initRadius过程负责确定每次增加请求半径。某个sink收到一个<saturated>消息之后重新设置其请求半径为某一较小值以试图缓解拥塞。 resetRadius过程负责在收到<saturated>消息之后计算新的请求半径。该sink随后进入算法的第二阶段。进入第二阶段的sink将周期性的试图增加其请求半径，以取得最优 max-min公平请求半径。此步骤由increaseRadius过程处理。这样增加的结果是，不久之后该sink再次收到<saturated>消息并缩小请求半径，而后再次周期性增加。

所有sink同时发出请求，并将初始半径设置为最小值。然后所有sink以同步方式增加请求半径直到网络中某一传感器节点上的数据流量饱和（该节点被称为瓶颈节点）。当某个传感器节点流量饱和时，覆盖该节点的所有sink停止增加其请求半径，但是其它sink继续增加其请求半径。当没有sink可以继续增加其请求半径时，算法结束。我们说此算法的解为最优解是因为该算法的解满足max-min公平性的同时被全局或局部最大化。