一文讲透自动驾驶中「过程噪音」与「测量噪音」的本质区别

「特性、影响及调控技术...」

噪音是指信号的随机误差。熟悉卡尔曼滤波的读者都会注意到里面有两个神秘的符号Q和R，分别代表过程噪音和测量噪音。但几乎所有的解读文章都视为理所当然不加解释。

在现代汽车工业中，传感器作为“感知器官”，其输出信号的准确性直接决定了车辆控制系统的性能与安全性。新兴的高级驾驶辅助系统（ADAS）与自动驾驶系统，以及最近兴起的具身机器人，都高度依赖传感器对车辆或者机器人状态、环境信息的精准采集。

然而，传感器信号在生成与传输过程中，不可避免地会受到各类噪音的干扰，其中过程噪音与测量噪音是两类最核心的干扰源。

本文将从定义界定、车辆影响、测定方式、动态调整及总结展望五个维度，系统地解释传感器的过程噪音与测量噪音。

在传感器信号处理领域，噪音通常被定义为“叠加在有效信号上的、无规律的干扰信号”，其存在会导致传感器输出与被测物理量的真实值产生偏差。

过程噪音与测量噪音的核心区别在于其来源与本质——前者源于被测对象自身的动态波动，是“信号本身的噪音”；后者源于传感器测量过程的固有缺陷，是“测量行为引入的噪音”（海森堡测不准原理？：））。

二者虽均表现为信号的随机波动，但在产生机制、统计特性及应对策略上存在显著差异。

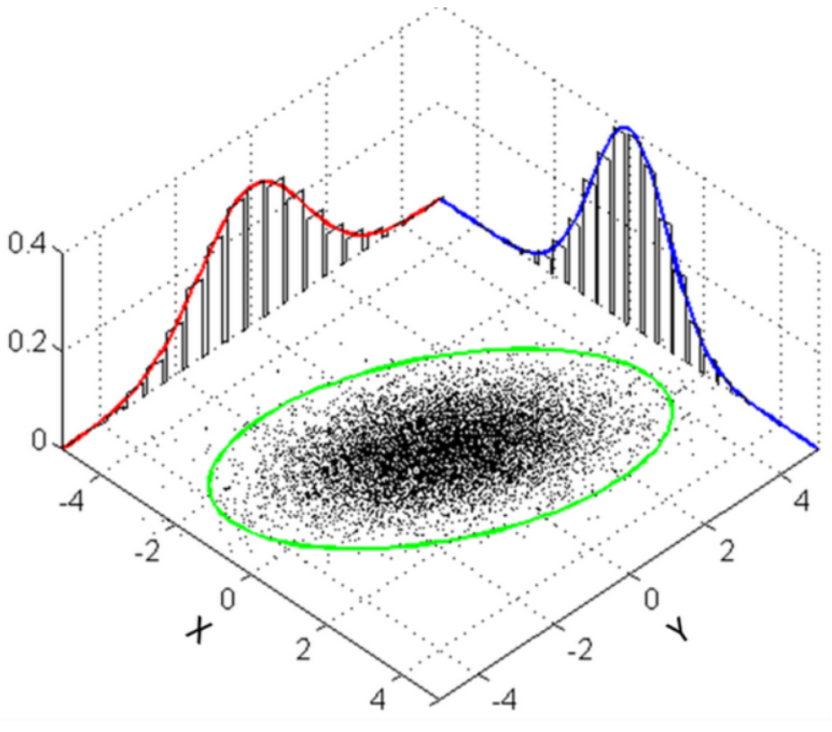
图1 | 两种噪音都服从的高斯分布，也就是正态分布

 1.1 过程噪音的本质与特征

过程噪音，又称“状态噪音”，是指被测物理量（即过程变量）自身在时间维度上的随机波动，与传感器的测量能力无关，是被测对象固有动态特性的体现。

从物理本质上看，过程噪音源于被测系统内部的随机扰动或外部环境的不确定性干扰，其大小与变化规律由被测过程的物理特性决定。

以车辆控制系统中的核心传感器为例，车速传感器所监测的“车速”这一物理量，其真实值并非恒定不变——即使驾驶员匀速踩下油门，发动机输出扭矩的微小波动、路面摩擦力的随机变化、传动系统的机械间隙等因素，都会导致车辆真实车速在目标值附近产生微小的、无规律的波动，这种波动就是车速信号的过程噪音。同样，在转向角传感器中，驾驶员手部的微小抖动、转向系统的弹性变形等，会导致转向角真实值产生随机波动，形成转向角信号的过程噪音。这种噪音会明显影响到自动驾驶、SLAM等等功能的精确执行。

过程噪音具有显著的统计特性：从时间域来看，其波动具有随机性，无法通过确定性函数预测，但在统计意义上服从特定的概率分布（如正态分布）；从频率域来看，其功率谱密度通常集中在特定频段，与被测过程的动态特性相关。

例如，车辆动力系统的过程噪音多集中在低频段（与发动机转速波动频率匹配），而底盘系统的过程噪音则可能覆盖中低频段（与路面激励频率相关）。此外，过程噪音的幅值与被测过程的工作状态密切相关，例如车辆在颠簸路面行驶时，车速与车身姿态的过程噪音幅值会显著大于在平坦路面行驶时。

 1.2 测量噪音的本质与特征

测量噪音是指传感器在将被测物理量转换为电信号（或其他可传输信号）的过程中，由于自身结构缺陷、信号转换原理限制或外部测量环境干扰而引入的随机误差，是“测量系统的噪音”。与过程噪音不同，测量噪音与被测物理量的真实值无关，仅反映传感器测量过程的精准度水平。

测量噪音的产生机制复杂，可分为内部来源与外部来源两类。内部来源主要包括：传感器敏感元件的固有噪声（如半导体元件的热噪声、压电元件的低频噪声）、信号调理电路的电子噪声（如运算放大器的失调噪声、电阻的热噪声）、模数转换（ADC）过程的量化噪声（将模拟信号转换为数字信号时的离散化误差）。外部来源主要包括：电磁干扰（如车辆高压线束产生的电磁场对传感器信号的干扰）、温度漂移（环境温度变化导致传感器敏感元件特性变化，引入额外误差）、机械振动（传感器安装基座的振动导致测量基准偏移）。

以车辆常用的毫米波雷达传感器为例，其测量噪音主要来源于：射频前端的热噪声、信号处理过程中的量化噪声，以及车辆电子系统产生的电磁干扰，这些噪音会导致雷达输出的目标距离、速度信号在真实值附近产生随机波动。而轮速传感器（如霍尔式轮速传感器）的测量噪音则主要包括：霍尔元件的开关噪声、信号传输线的电磁干扰噪声，以及由于齿轮齿形误差导致的脉冲信号波动，这些噪音会影响轮速计算的精准度。

测量噪音同样具有明确的统计特性：多数情况下服从正态分布，其幅值大小可用“信噪比（SNR）”“均方根误差（RMSE）”等指标量化。与过程噪音相比，测量噪音的频率特性更复杂，可能覆盖从低频到高频的宽频段，例如电子元件的热噪声通常为白噪声（功率谱密度在全频段均匀分布），而温度漂移引入的噪音则多为低频噪音。此外，测量噪音的特性与传感器的工作状态（如供电电压、工作温度）密切相关，例如当传感器工作温度超出额定范围时，测量噪音的幅值会显著增大。

车辆运动控制系统是一个典型的“感知-决策-控制”闭环系统，传感器信号的准确性直接决定了控制指令的合理性。过程噪音与测量噪音虽来源不同，但都会导致传感器输出信号偏离真实值，进而通过闭环控制链路影响车辆的运动状态，可能引发控制精度下降、系统稳定性降低甚至安全风险。

高级驾驶辅助系统（ADAS）与自动驾驶系统（L2及以上级别）依赖多传感器融合技术（摄像头、毫米波雷达、激光雷达、超声波雷达等）感知车辆周围环境与自身状态，其对传感器信号的噪音更为敏感——噪音干扰可能导致环境感知错误，进而引发决策失误，带来严重的安全风险。

过程噪音与测量噪音对这类系统的影响主要体现在“环境感知偏差”与“路径规划失误”两个层面。

 2.1 环境感知偏差：目标识别错误与距离判断失准

ADAS系统中的自适应巡航（ACC）、自动紧急制动（AEB）功能，依赖毫米波雷达与摄像头融合采集前方车辆的距离、速度信息。毫米波雷达的距离测量噪音（源于射频信号的热噪声与量化噪声）与速度信号的过程噪音（源于前方车辆的微小加减速），会导致系统对前方车辆状态的判断出现偏差：

当测量噪音导致雷达输出的“前车距离”信号在真实值附近大幅波动时，ACC系统可能将这种波动误判为前车的“急减速”，从而错误地执行自身车辆的减速指令，导致车辆行驶速度频繁波动，影响乘坐舒适性；若噪音导致系统低估前车距离，则可能在AEB功能触发时出现“制动过晚”的情况，增加追尾风险。

对于自动驾驶系统的激光雷达，其点云数据的过程噪音（源于目标物体表面的粗糙度导致的反射信号波动）与测量噪音（源于激光接收器的电子噪声），会导致点云聚类错误——例如将路边的行人与护栏误判为一个整体目标，或遗漏近距离的小型障碍物（如石块），这些感知错误会直接导致系统的决策逻辑失效，引发碰撞风险。

 2.2 路径规划失误：定位偏差与轨迹偏移

自动驾驶系统的路径规划依赖高精度定位传感器（如GNSS、IMU惯性测量单元）与环境地图的匹配，传感器信号的噪音会导致车辆定位偏差，进而引发路径规划失误。IMU传感器的加速度与角速度信号中，过程噪音源于车辆自身的振动与颠簸，测量噪音源于陀螺与加速度计的固有噪声，这些噪音会通过积分运算被放大——例如，角速度信号的微小噪音经过积分计算车辆姿态角时，会导致姿态角误差随时间累积，进而使车辆的定位结果偏离真实位置。

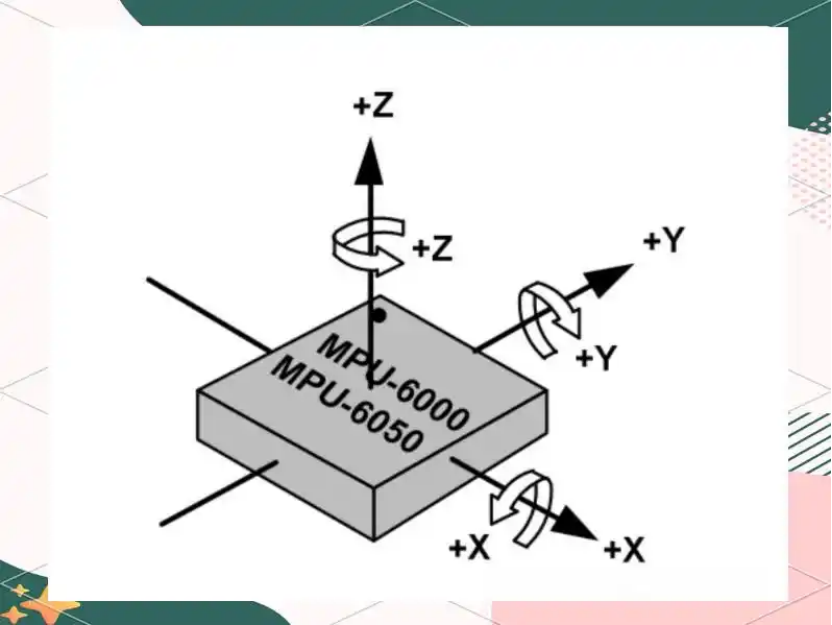
图2 | IMU示意图，测量车辆位姿，来自网络

在城市道路行驶场景中，若定位偏差导致系统误判车辆处于“车道中央”，而实际车辆已接近车道边缘，系统可能不会及时输出转向修正指令，导致车辆偏离车道；在路口转弯场景中，定位偏差可能导致系统误判转弯时机，引发转向过早或过晚，增加与侧向车辆碰撞的风险。

传感器噪音的测定是实现噪音抑制与控制的前提，其核心目标是通过实验手段分离过程噪音与测量噪音，量化二者的统计特性（如均值、方差、功率谱密度）。在工程实践中，为简化控制系统的设计，理想状态下通常假设过程噪音与测量噪音的统计特性（如方差）是恒定不变的，这种假设虽与实际情况存在差异，但为控制器参数的整定提供了重要的理论基础。

过程噪音与测量噪音的统计特性恒定不变，这也是卡尔曼滤波的基本假设之一。

 3.1 过程噪音的测定方式

过程噪音是被测物理量自身的波动，其测定的核心难点在于“如何排除测量噪音的干扰，获取被测物理量的真实值”。由于真实值无法直接测量，工程中通常采用“高精度基准对比法”或“多传感器融合法”间接分离过程噪音，常用的测定方式包括静态测定与动态测定两类。

3.1.1 静态测定：适用于稳态过程的噪音量化

当被测过程处于静态或准静态状态时（如车辆静止时的车身姿态），被测物理量的真实值理论上恒定不变，此时传感器输出信号的波动主要由测量噪音与低频过程噪音组成。通过采用精度远高于被测传感器的“基准传感器”同时采集同一物理量，可实现过程噪音的分离。

静态测定的优势在于实验条件易控制，噪音分离精度高；缺点是仅适用于稳态工况，无法反映动态过程中过程噪音的变化特性。

3.1.2 动态测定：适用于瞬态过程的噪音量化

当被测过程处于动态状态时（如车辆加速时的车速、转向时的转向角），被测物理量的真实值随时间变化，此时需采用“多传感器融合法”或“系统辨识法”分离过程噪音。多传感器融合法的核心思想是：

采用多个不同类型、不同测量原理的传感器采集同一物理量，由于不同传感器的测量噪音相互独立，通过卡尔曼滤波、加权平均等融合算法，可抑制测量噪音，得到更接近真实值的融合信号，进而计算过程噪音。

比如自动驾驶的路径规划，不止规划路线，还会规划每一点的速度，因此精确的加减速十分重要。

以车辆加速过程中车速的过程噪音测定为例，测定步骤如下：

1）同时采用轮速传感器、GPS车速传感器、惯性测量单元（IMU）三种传感器采集车速信号，三种传感器的测量原理不同（轮速传感器基于机械转动，GPS基于卫星定位，IMU基于加速度积分），测量噪音具有独立性；

2）设计卡尔曼滤波融合算法，将三路传感器信号作为输入，输出融合后的车速信号（近似真实值）；

3）计算每路传感器信号与融合信号的差值，得到各路传感器的测量噪音；

4）计算融合信号自身的波动量，即为车速的过程噪音。为确保测定精度，需在不同加速工况（如缓加速、急加速）下重复实验，以获取过程噪音的统计特性。

 3.2 测量噪音的测定方式

测量噪音是传感器测量过程引入的干扰，其测定的核心是“将被测物理量的真实值固定，使传感器输出信号的波动仅由测量噪音引起”。工程中通常采用“标准信号源法”或“静态环境法”实现这一目标，具体测定方式包括实验室测定与车载测定两类。

3.2.1 实验室测定：高精度标准环境下的噪音量化

实验室测定是测量噪音测定的主要方式，通过构建标准的物理量环境（如标准温度、标准压力、标准转速），使被测物理量的真实值恒定且已知，从而直接获取测量噪音。常用的实验设备包括标准信号发生器、高精度校准台等。

车速信息对自动驾驶是核心参数，车辆轮速是车数的衡量之一（另外的还有GPS车速）。

以霍尔式轮速传感器的测量噪音测定为例，实验室测定步骤如下：

1）将轮速传感器安装在高精度电动校准台上，校准台可精确控制齿轮的转速（真实值已知）；

2）将校准台设定为不同的转速工况（如100rpm、500rpm、1000rpm），保持工况稳定；

3）采集传感器的输出脉冲信号，通过信号处理将脉冲信号转换为转速值；

4）计算传感器输出转速与校准台标准转速的差值，该差值即为不同转速工况下的测量噪音；

5）对测量噪音进行统计分析，计算其均值（反映系统误差）、方差（反映随机误差）及功率谱密度（反映频率特性），完成测量噪音的量化。

为模拟车辆实际工作环境，实验室测定还需考虑温度、电磁干扰等因素的影响——例如，通过高低温试验箱改变传感器的工作温度，通过电磁干扰发生器模拟车辆的电磁环境，测定不同环境条件下测量噪音的变化特性，为后续的动态调整提供依据。

3.2.2 车载测定：实际工作环境下的噪音验证

实验室测定虽精度高，但无法完全模拟车辆复杂的实际工作环境（如剧烈振动、多源电磁干扰），因此需要通过车载测定验证测量噪音的特性。车载测定通常采用“同一传感器冗余布置法”，即在车辆上安装两个型号、规格完全相同的传感器，同时采集同一物理量，基于两路信号的相关性分离测量噪音。

以车辆横向加速度传感器的车载测定为例，测定步骤如下：

1）在车辆同一位置安装两个相同的横向加速度传感器，确保二者的安装姿态与环境完全一致；

2）车辆在不同路面（平坦路面、颠簸路面）、不同行驶工况（直线行驶、转弯行驶）下行驶，同步采集两路传感器的输出信号；

3）由于两路传感器采集的是同一物理量，其过程噪音成分完全相同，而测量噪音成分相互独立；

4）通过计算两路信号的协方差与方差，可分离出测量噪音的方差（计算公式为：测量噪音方差=（传感器1方差+传感器2方差-2×协方差）/2）；

5）基于不同工况下的测量噪音数据，验证实验室测定结果的准确性，并补充极端工况下的噪音特性。

 3.3 理想状态下的噪音假设

在车辆控制系统设计中，为简化控制器的设计与参数整定，理想状态下通常对过程噪音与测量噪音做出“统计特性恒定”的假设，即认为二者均为“零均值、方差恒定的高斯（正态分布）白噪声”。这一假设的依据主要有两点：

一是在短时间内，被测过程的工作状态相对稳定（如车辆匀速行驶时），过程噪音的波动范围有限，统计特性近似恒定；

二是传感器的工作环境（如温度、供电电压）在设计范围内相对稳定，测量噪音的统计特性也近似恒定。

这一假设为经典控制理论与滤波算法的应用提供了便利。例如，在卡尔曼滤波算法中，需要预先设定过程噪音协方差矩阵（Q矩阵）与测量噪音协方差矩阵（R矩阵），理想状态下可通过前文所述的测定方式获取Q与R的固定值，代入算法中实现对噪音的有效抑制。在PID控制器设计中，固定的噪音特性可帮助工程师确定合适的比例系数与积分时间，避免控制器对噪音产生过度响应。

需要强调的是，理想状态的假设仅为工程简化，实际车辆行驶过程中，工况的动态变化（如加速、制动、转弯）与环境的不确定性（如路面变化、电磁干扰增强），都会导致过程噪音与测量噪音的统计特性发生动态变化，因此需要在实际系统中引入动态调整机制。

现实车辆行驶环境中，过程噪音与测量噪音的统计特性会随工况、环境的变化而动态改变——例如，车辆从平坦路面驶入颠簸路面时，车速与车身姿态的过程噪音幅值会增大；传感器工作温度升高时，测量噪音的方差会显著增加。若仍采用理想状态下的固定参数控制策略，会导致噪音抑制效果下降，甚至引发系统不稳定。

因此，工程中通常采用“硬件优化+软件自适应”的协同方案，实现对两种噪音的动态调整与抑制。

 4.1 硬件层面的动态调整：从源头抑制噪音变化

硬件层面的动态调整主要通过优化传感器结构设计、增强环境适应性或引入主动补偿机制，从源头降低噪音的动态波动，其核心目标是使传感器在不同工况下的测量噪音特性保持相对稳定，减少对软件调整的依赖。

4.1.1 传感器结构优化：提升环境适应性

针对测量噪音随环境变化的问题，通过优化传感器的敏感元件结构、信号调理电路设计，可提升其对温度、振动、电磁干扰的抵抗能力。

例如，在温度适应性设计方面，采用“温度自补偿”结构——在传感器敏感元件旁集成温度传感器，实时采集工作温度，通过硬件电路或嵌入式算法对测量信号进行温度补偿，抑制温度漂移引入的测量噪音；

在电磁干扰抑制方面，采用“差分信号传输”设计——传感器输出信号采用差分形式传输，利用差分信号对共模干扰的抑制能力，降低电磁干扰导致的测量噪音波动。

4.1.2 主动减震与抗干扰设计：抑制外部环境引发的噪音

过程噪音与测量噪音的动态波动，很大程度上源于车辆行驶过程中的振动与电磁干扰，因此通过主动减震与抗干扰设计，可从外部环境层面抑制噪音的变化。

在振动抑制方面，传感器的安装基座采用“主动减震机构”——例如，在毫米波雷达的安装支架上集成压电减震器，通过传感器采集车身振动信号，控制压电减震器产生反向振动，抵消支架的振动，从而减少振动导致的测量噪音与过程噪音波动；

在电磁干扰抑制方面，采用“主动电磁屏蔽”技术——在传感器信号传输线上缠绕磁环，同时在车辆高压线束与传感器线束之间设置主动干扰抵消器，通过产生反向电磁场抵消高压线束产生的电磁干扰，稳定测量噪音的幅值。

 4.2 软件层面的动态调整：自适应算法实现噪音精准抑制

软件层面的动态调整是应对噪音特性变化的核心手段，其核心思想是通过实时监测传感器信号的统计特性，动态调整滤波算法参数或控制器参数，实现对过程噪音与测量噪音的自适应抑制。常用的技术包括自适应滤波算法、智能算法与多传感器融合技术。

4.2.1 自适应滤波算法：动态调整滤波参数

传统的固定参数滤波算法（如低通滤波、卡尔曼滤波）在噪音特性变化时，滤波效果会显著下降——例如，固定截止频率的低通滤波，在过程噪音高频分量增加时，无法有效抑制高频噪音；

固定Q、R矩阵的卡尔曼滤波，在测量噪音方差增大时，会导致滤波结果偏离真实值。自适应滤波算法通过实时估算噪音的统计特性，动态调整滤波参数，从而提升不同工况下的滤波效果。

图3 | Matlab Simulink用户对各种滤波器非常熟悉

常用的自适应滤波算法包括自适应卡尔曼滤波、最小均方误差（LMS）滤波等。以自适应卡尔曼滤波为例，其核心改进是在传统卡尔曼滤波的基础上，增加了“噪音协方差矩阵估算模块”——通过实时采集传感器输出信号，采用递推最小二乘法或贝叶斯估计法，动态估算过程噪音协方差矩阵Q与测量噪音协方差矩阵R，并将估算结果实时更新到卡尔曼滤波的预测与更新方程中，实现滤波增益的动态调整。

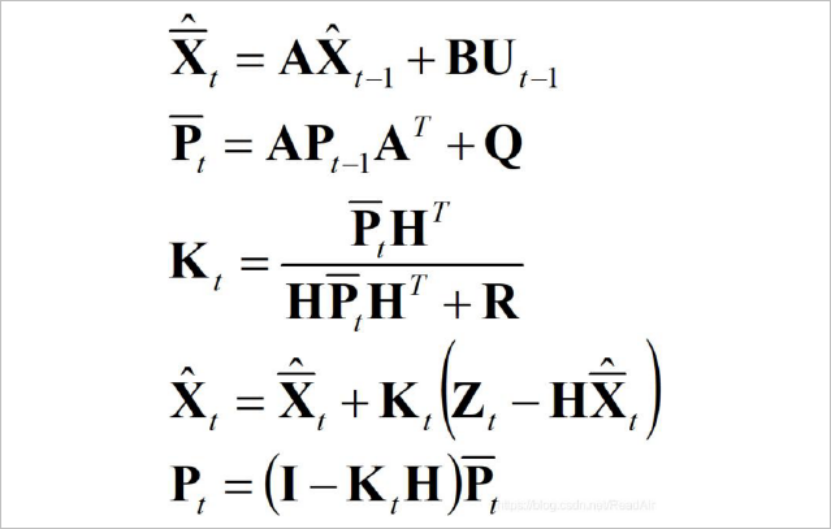
图4 |卡尔曼滤波的经典五公式

例如，当车辆驶入颠簸路面时，过程噪音的方差增大，算法通过估算发现Q矩阵增大，会自动增大滤波增益中预测误差的权重，从而提升对过程噪音的抑制效果；当传感器受到强电磁干扰时，测量噪音的方差增大，算法通过估算发现R矩阵增大，会自动减小滤波增益中测量信号的权重，避免测量噪音对滤波结果的影响。

4.2.2 智能算法：实现复杂噪音特性的动态适应

对于具有非线性、时变特性的复杂噪音（如车辆在极端工况下的噪音），传统的自适应滤波算法难以精准建模，此时可采用神经网络、模糊控制等智能算法实现动态调整。这类算法的优势在于无需建立精确的数学模型，可通过大量数据训练学习噪音的变化规律，实现对噪音的自适应抑制。

以神经网络自适应滤波为例，其实现过程包括：

1）离线训练阶段：采集不同工况下的传感器信号（含噪音）与对应的真实值（通过基准传感器获取），构建训练数据集，训练神经网络模型（如BP神经网络、RBF神经网络），使模型学习“噪音特性-滤波参数”之间的映射关系；

2）在线应用阶段：实时采集传感器信号，通过神经网络模型估算当前噪音的统计特性（如方差、频率），并输出对应的最优滤波参数（如低通滤波的截止频率、卡尔曼滤波的Q/R矩阵）；

3）动态调整阶段：将最优滤波参数实时更新到滤波算法中，实现对当前噪音的精准抑制。例如，在自动驾驶车辆的激光雷达点云降噪中，采用深度学习模型（如PointNet）实时识别点云数据中的噪音特征，动态调整点云聚类的阈值参数，可有效滤除不同环境下（如雨天、雾天）的点云噪音，提升目标识别精度。

4.2.3 多传感器融合技术：通过信息冗余实现噪音动态抑制

多传感器融合技术通过融合不同类型传感器的信号，利用各传感器噪音的独立性与互补性，实现对过程噪音与测量噪音的动态抑制。其核心优势在于：当某一传感器的噪音特性发生恶化时，其他传感器的信号可对其进行补偿，确保融合后信号的稳定性。

在车辆定位系统中，多传感器融合技术的应用最为典型——融合GNSS、IMU、轮速传感器与视觉传感器的信号，动态抑制各类噪音。

例如，当车辆行驶至隧道等GNSS信号遮挡区域时，GNSS的测量噪音急剧增大，融合算法会自动降低GNSS信号的权重，提升IMU与轮速传感器信号的权重，利用IMU的短期高精度特性与轮速传感器的实时性，维持定位精度；

当车辆行驶在颠簸路面时，IMU的过程噪音增大，算法会提升GNSS与视觉传感器信号的权重，利用GNSS的长期稳定性与视觉传感器的环境匹配能力，补偿IMU的误差。通过动态调整各传感器的融合权重，可实现不同工况下噪音的自适应抑制，确保定位信号的稳定性。

传感器的过程噪音与测量噪音是影响车辆控制系统性能的核心干扰因素，二者虽来源不同——过程噪音是被测物理量自身的随机波动，测量噪音是传感器测量过程引入的误差，但都会通过“感知-决策-控制”闭环链路影响车辆的运动状态，可能引发自动驾驶系统的感知与决策失误。因此，深入理解两种噪音的本质特征、精准测定其统计特性，并采取有效的动态调整措施，对于提升车辆控制系统的性能与安全性具有重要意义。

本文通过对两种噪音的系统剖析，可得出以下结论：

第一，过程噪音与测量噪音的本质差异决定了其应对策略的不同。过程噪音是被测对象的固有属性，与传感器无关，其特性与被测过程的工况密切相关；测量噪音是传感器的固有属性，与被测对象无关，其特性与传感器的工作环境（温度、振动、电磁干扰）密切相关。这种本质差异导致过程噪音的抑制需从优化被测系统的动态特性入手，而测量噪音的抑制则需从提升传感器自身的测量精度与环境适应性入手。

第二，理想状态下的“噪音特性恒定”假设是工程简化的重要手段，但需明确其局限性。该假设为控制器与滤波算法的参数整定提供了理论基础，在短时间、稳定工况下具有较好的适用性；但在实际车辆行驶过程中，工况与环境的动态变化会导致两种噪音的特性发生显著改变，因此必须采用动态调整措施，才能确保系统性能的稳定性。

第三，“硬件优化+软件自适应”的协同是应对噪音动态变化的有效途径。硬件层面通过优化传感器结构、采用主动减震与抗干扰设计，可从源头降低噪音的动态波动；软件层面通过自适应滤波算法、智能算法与多传感器融合技术，可实现对噪音特性变化的精准适应，二者协同作用，可实现不同工况下噪音的高效抑制。

传感器的过程噪音与测量噪音的研究是车辆工程领域的永恒课题，其研究成果不仅可推动传感器技术与车辆控制技术的发展，还可为自动驾驶系统的安全落地提供重要保障，具有重要的理论价值与工程意义。在未来的研究中，需进一步加强多学科交叉融合，结合机械工程、电子工程、控制科学与人工智能等领域的先进技术，实现对两种噪音的更精准测定与更高效控制，为车辆工业的高质量发展提供支撑。

「点击加入交流群」