又一篇Science子刊！浙大高飞团队提出分层规划系统：仅0.01秒生成山地最优航迹！

最新推荐文章于 2025-07-22 21:26:13 发布

深蓝学院

最新推荐文章于 2025-07-22 21:26:13 发布

阅读量1.8k

点赞数 17

CC 4.0 BY-SA版权

文章标签：机器人无人机

本文链接：https://blog.youkuaiyun.com/soaring_casia/article/details/148878155

摘要

在智能机器人与自动驾驶技术飞速发展的当下，让机器人在复杂多变的环境中展现出如同人类般的敏捷导航能力，仍然是科学界面临的一项艰巨挑战。传统路径规划算法在面对错综复杂的环境时，往往效率会显著下降，计算和内存需求也会随之增加。

©️【深蓝AI】编译

这与人类在导航方面的卓越表现形成鲜明对比，人类凭借其出色的空间感知和经验积累，能够直观地识别可行路径。受此启发，浙江大学高飞团队提出了一种创新性的分层运动规划系统。该系统巧妙地结合了前端路径规划的深度学习能力与后端轨迹优化的数值稳定性，旨在模拟人类“高层规划，低层调整”的导航框架。

通过这种方式，研究不仅突破了传统算法在复杂场景下的性能瓶颈，更从根本上解决了现有轨迹优化方法中存在的奇点问题，确保了复杂机动场景下的运动连续性和可行性。本文将深入探讨这一AI赋能的分层运动规划新范式，解析其如何通过模仿人类智慧，为未来机器人稳定、高效、智能地在复杂环境中自主导航奠定基础。

《Hierarchically Depicting Vehicle Trajectory with Stability in Complex Environments》于2025年6月19日刊登在机器人领域权威期刊Science Robotics。第一作者为浙江大学控制科学与工程学院博士研究生韩志超，通讯作者为浙江大学长聘副教授、博导高飞。

本文由paper通讯作者——高飞授权【深蓝AI】发布！

论文题目：Hierarchically depicting vehicle trajectory with stability in complex environments

论文作者：Zhichao Han, Mengze Tian, Zaitian Gongye, Donglai Xue, Jiaxi Xing, Qianhao Wang, Yuman Gao, Jingping Wang, Chao Xu, Fei Gao

论文地址：

https://www.science.org/doi/10.1126/scirobotics.ads4551

本研究提出了一种创新性的分层运动规划系统，其核心在于模仿人类“高层规划、低层调整”的导航策略，并巧妙地融合了深度学习与数值优化的优势。整个系统由两个核心模块组成：负责生成粗略拓扑路径的“前端路径规划器”（Front End）和负责将粗略路径精炼为高质量、符合运动学约束的“后端轨迹优化器”（Back End）。总体框架如下图所示：

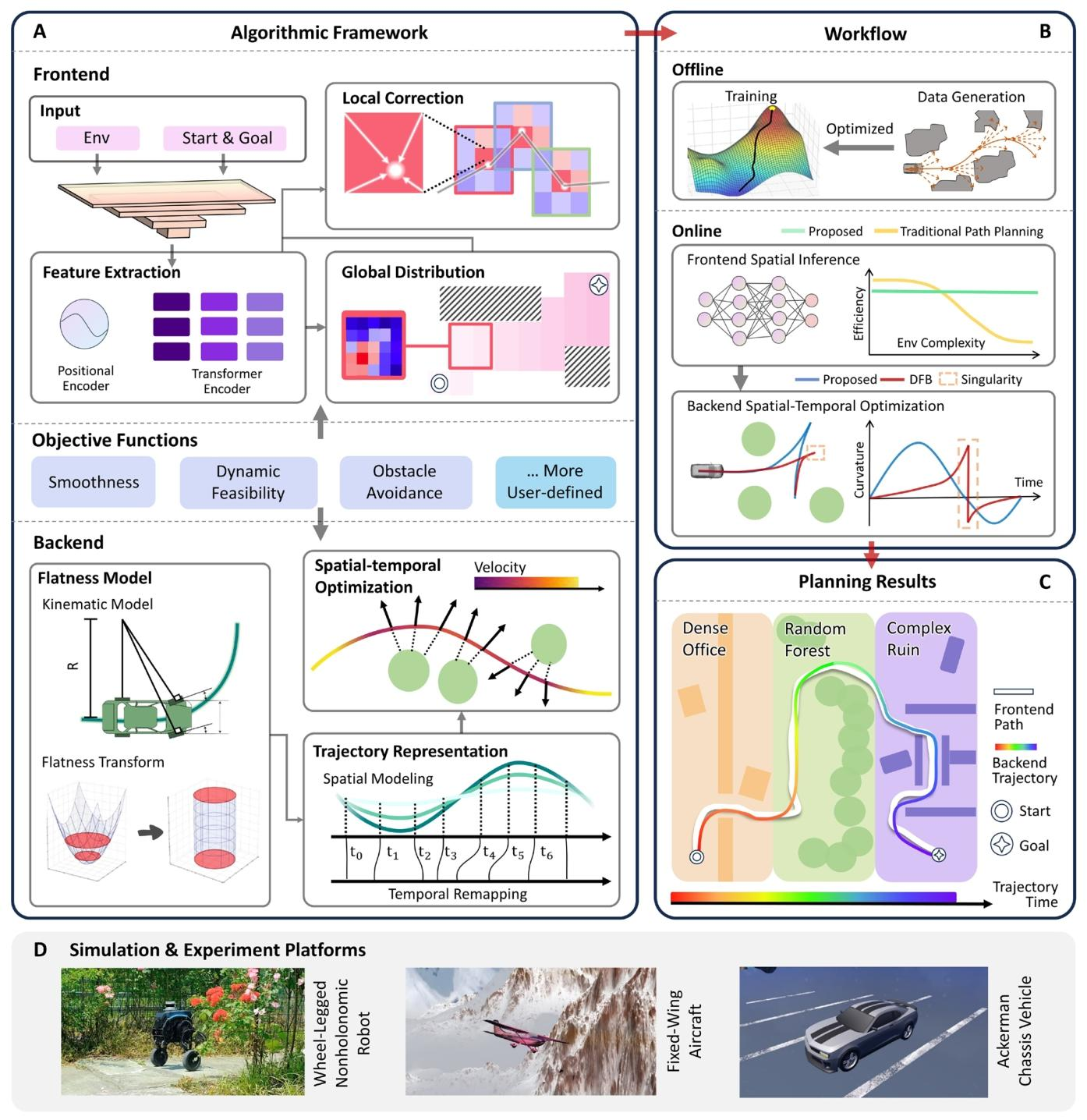
图1：分层运动规划系统框架

前端路径规划器：模拟人类直觉的神经网络路径生成

前端模块旨在模拟人类直观的寻路能力，通过神经网络直接从环境信息和经验中学习，快速识别可行的全局路径。其关键特点和技术细节包括：

1. 人类直觉启发式设计：区别于传统搜索或采样算法，前端路径规划器受人类“给定地图，即使是小孩也能直观描绘路线”的启发，利用神经网络直接绘制起始点到终点之间的曲线路径，从而高效地描绘出合理的路径，不受环境几何复杂度的影响。

2. 输入和编码：网络输入为尺寸为 H×W 的栅格化环境信息（通常表示为ESDF，即欧几里得符号距离场），以及起始点和目标点的 SE(2) 状态（位置和方向角）。通过独特的编码策略，将起始点和目标点高亮显示在张量上，并引入额外张量表示方向角的余弦和正弦值，最终形成 4×H×W 的输入张量。

3. 三阶段网络架构：整个网络由特征提取层（FEL），全局分布层 (GDL)以及局部校正层 (LCL)这三个主要组件构成。特征提取层 (FEL）用于将路径规划问题编码到高维潜在空间中，并通过Transformer编码器提取高级特征。全局分布层 (GDL）推断路径上每个状态点在预定义区域提议上的概率分布，以估计点的粗略空间分布。局部校正层 (LCL)结合环境特征和GDL的概率分布，进一步精确计算状态点的位置和姿态。网络的训练主要通过监督学习的方式，模仿由高精度离散化搜索和后端优化生成的“真值”轨迹行为，直接输出初始引导路径，避免了耗时的采样和搜索过程，实现了近乎恒定的推理时间。

4. 损失函数设计: 前端路径规划器的损失函数综合考虑了监督项(模仿真值)和无监督项(路径有效性)。这种设计使得网络能够更好地发现训练数据中潜在的因果关系。损失函数 $L$ 的整体表达式为：

后端轨迹优化器：数值稳定的双层多项式轨迹表示

后端模块负责将前端生成的粗略路径精炼为符合系统高阶运动学约束、平滑且无碰撞的时空最优轨迹。其创新点在于解决了传统微分平坦模型在速度为零时出现的奇点问题，显著增强数值稳定性。

1. 微分平坦性重映射：现有轨迹优化方法虽然利用微分平坦性可以有效加速优化过程并消除运动方程约束，但在车辆速度接近零时（如换向或停车），会遇到奇点问题。这导致一些状态（如偏航角）无法准确推导，进而造成数值不稳定性和约束违反。本研究引入了一个“伪弧”作为中间变量，将平坦输出表示为伪弧的函数，同时伪弧再表示为时间的函数。通过这种双层映射，即使机器人实际速度为零，伪速度仍可保持非零，从而使得计算转向角和转向角速率的表达式分母始终严格为正，从数学上根除原始奇点问题。

2. 非线性约束优化: 后端轨迹优化问题被表述为一个非线性约束优化问题，其目标是在满足各种运动可行性约束的前提下，最小化轨迹的控制能量并对总时长进行正则化。

优化目标函数 $I$ 旨在最小化轨迹的能量消耗和总时长，其表达式如下:

$\min_{c^p, c^s, \delta s, \delta T \in \mathbb{R}^+} J = \int_0^{T_s} \sigma_t^{(u)}(t)^T \sigma_t^{(u)}(t) dt + \rho T_s$

同时需要满足边界条件 $B(\sigma_t(0) \dots \sigma_t^{(u-1)}(0), \sigma_t(T_s) \dots \sigma_t^{(u-1)}(T_s)) = 0,$

确保轨迹在起点和终点处的状态符合要求，连续性约束 $\mathcal{T}(\gamma_1 \dots \gamma_M, s_1 \dots s_M, \delta s, \delta T) = 0,$

段多项式轨迹在各个连接点处的平滑过渡，最小伪速度约束 $||\dot{\gamma}_s(s(t))||_2 > \alpha$ ，确保伪速度大于一个设定的阈值伪速度从而进一步避免奇点问题，非负约束 $\dot{s}_t(t) \geq 0$ ，确保伪速度始终为正值，运动学与避障约束 $\mathcal{G}\left(\gamma(s(t)), ..., \gamma_{| s}^{(u)}(s(t)), s(t), ..., s_{| t}^{(u)}(t)\right) \preceq 0$ ，包含最大速度、最大加速度、最大转向角、最大转向角速率以及障碍物规避等常见的运动学和环境约束。

本研究通过一系列全面的模拟和真实世界实验，验证了所提出的分层运动规划系统在复杂环境下的卓越性能和鲁棒性。实验不仅量化了其在计算效率和时间稳定性方面的优势，更突出了其在解决轨迹优化中长期存在的奇点问题上的突破。

为了验证前端方法的效率和时间稳定性，研究团队在多种复杂场景下，使用Ackermann转向车辆进行了对比实验，包括包含不规则障碍物的“随机森林”、具有狭窄通道的“密集办公室”以及机器人常需绕道的“复杂废墟”场景。结果显示，本模型生成的路径比Hybrid A和THybrid A算法更平滑，且更接近真值轨迹，这得益于其直接监督轨迹生成过程，无需耗时的搜索。本算法在各种环境下均保持了高成功率和低计算时间，而其他算法随着环境复杂度增加，计算时间显著增加且稳定性较差。此外，本方法生成的初始路径作为后端优化的输入时，所需优化时间显著更少，即可达到高质量轨迹。这些量化结果清晰展示了本方法在效率和稳定性上的优势。

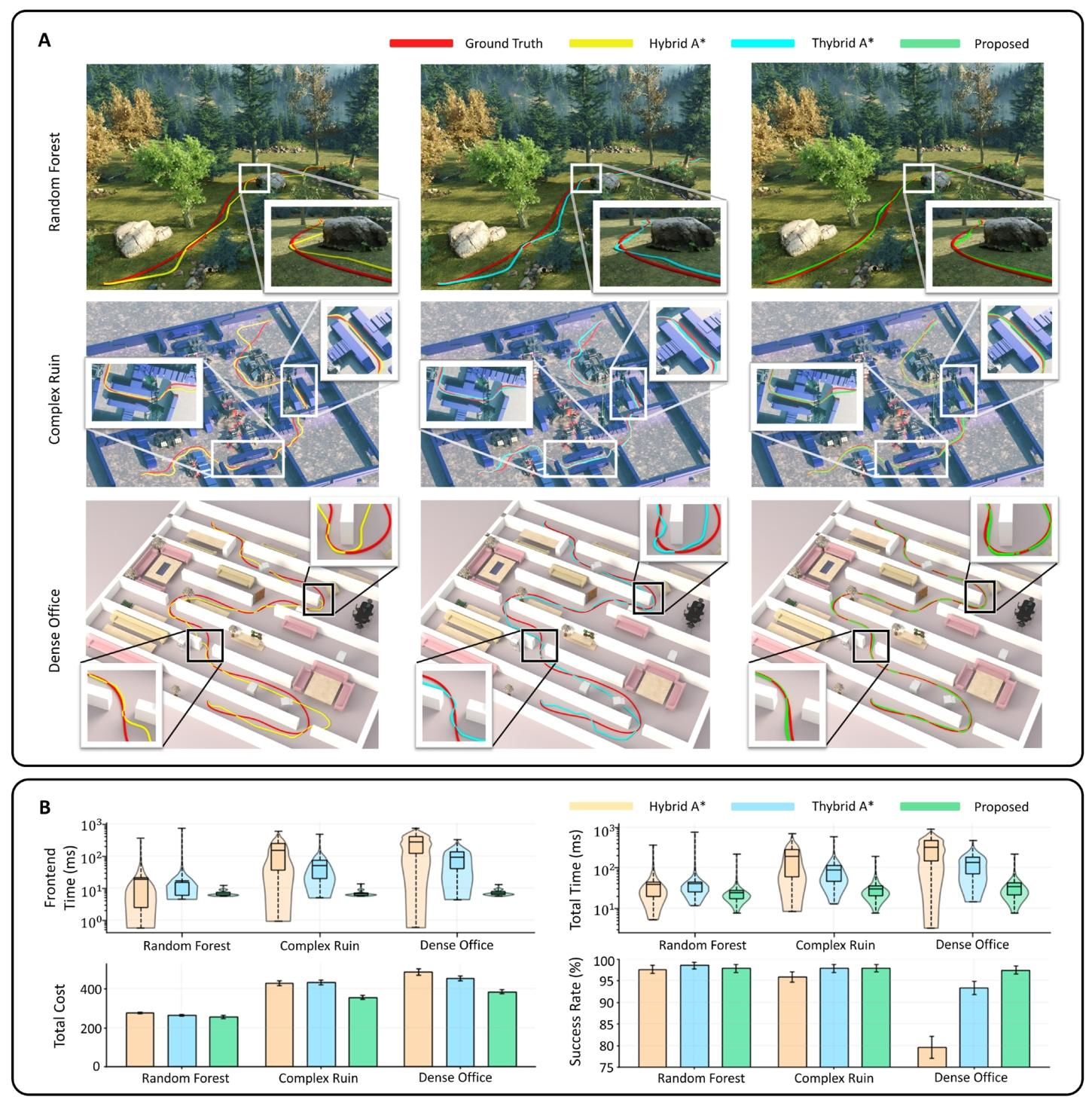
图2：各种复杂场景下的时间稳定性。（A）实验环境和规划结果。（B）使用小提琴图和条形图进行的指标比较。总时间为前端和后端时间之和。总损失为后端优化的能量损失和时间损失之和。成功率由优化后的轨迹是否避开障碍物定义。如果轨迹避开障碍物，则该情况被视为成功；否则被视为失败。

研究进一步验证了前端规划器与地形高程图的兼容性，并将其扩展应用于大规模固定翼飞机导航任务。在穿越山区和丘陵地形的场景中，本算法在不到10毫秒内找到了接近最优的解决方案，其路径质量与经典的RRT*算法相当，但计算时间却少了一个数量级。实物实验证明，神经网络生成的飞行路径作为有效航点，成功引导固定翼飞机无碰撞地穿越山丘，甚至能无缝穿过山峰之间的鞍部。

图3：山地地形中的固定翼导航。（A）固定翼飞行在 Unity3D 中的可视化效果。（B）路径点处的地形海拔。在有限时间内由 RRT生成的路径并非最优，可能导致固定翼飞机飞得离下方地形过近，从而使飞行不安全。（C）本研究的方法与 RRT在不同计算时间下关于高度成本和长度成本的对比分析。（D）规划场景的地形高程图。（E）1000 米 ×50 米的固定翼巡航实验。固定翼飞机沿着航路点飞行，避开飞行过程中遇到的山峰。固定翼飞机的最小转弯半径为 50 米，飞行高度为 55 米。使用 GPS 进行定位和导航。

本研究还在具有挑战性的多向倒车场景中严格验证了后端轨迹优化算法的数值稳定性。在模拟停车场场景中，基线微分平坦度规划由于奇点存在导致轨迹更复杂，而本方法生成的轨迹明显更平滑。实验结果表明，基线DFB在速度为零时存在计算奇点，即使设置非零小速度，也可能导致转向角速率和转向角约束被违反，甚至引起机械部件剧烈振动。相比之下，本方法始终表现出良好的数值稳定性，确保了平滑的速度曲线，并能稳定收敛到动态可行的解决方案。本方法与基线DFB相比，最大位置跟踪误差降低了38.2%，最大角度跟踪误差降低了57.7% 。

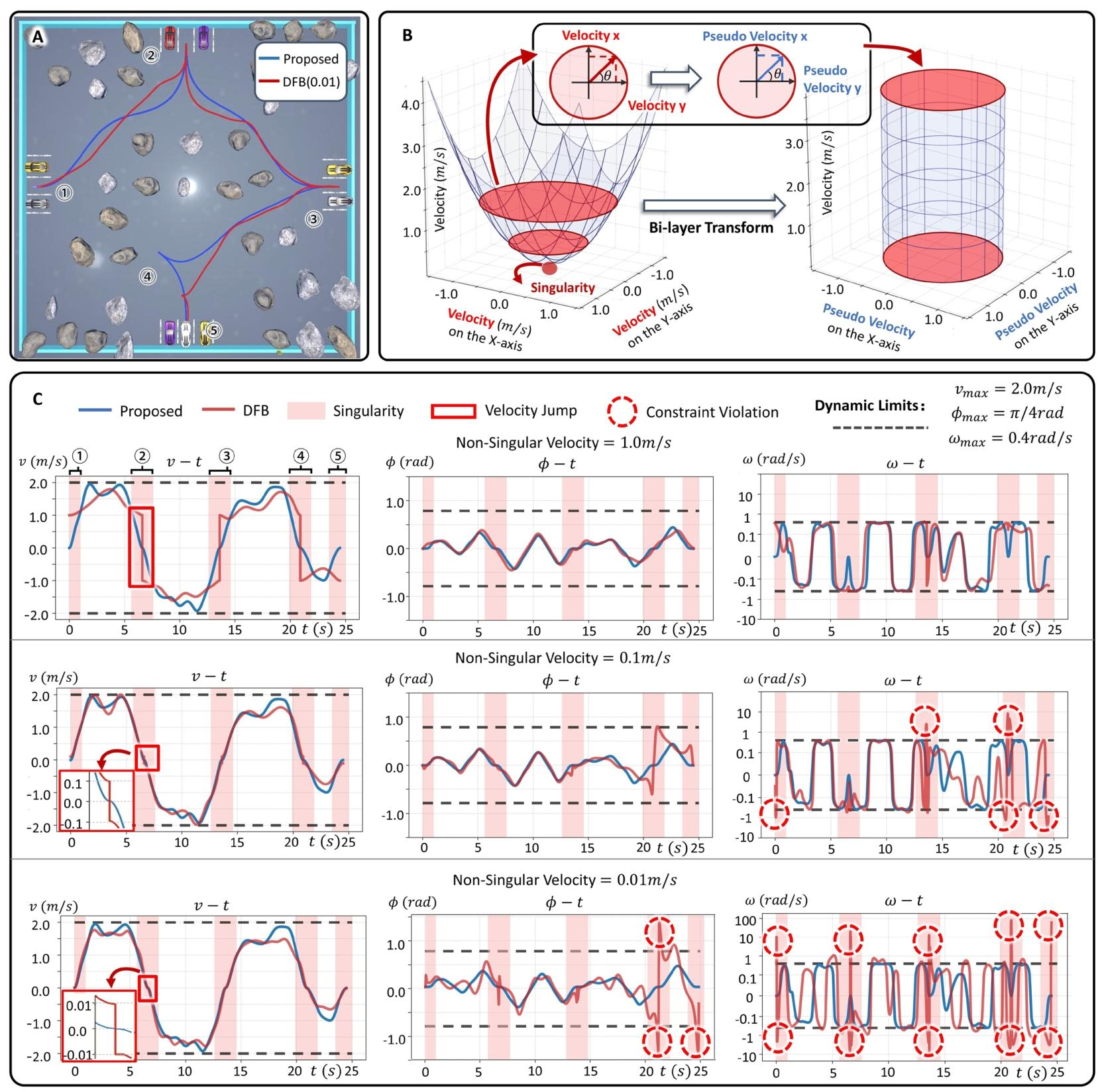
图4：多次倒车场景下的数值稳定性。（A）规划轨迹的可视化。在此处的 DFB 方法中，为避免计算奇点，将前进与后退运动的切换速度设为 0.01 m/s。（B）平坦空间中奇点消除的可视化。在变换前，当车辆速度为 0 m/s 时会出现奇点，导致无法计算车辆航向角。然而，通过采用本研究的双层变换并引入伪速度，伪速度的大小始终超过阈值，从而无论实际速度如何，均可在不遭遇奇点的情况下恢复车辆航向角。（C）本研究的轨迹与 DFB 在不同参数下生成的轨迹之间的速度、转向角和转向角速率曲线对比。图中黑色虚线表示动态约束条件。

最后，为了验证规划器的实用性，研究将其部署在一个约 50 m×25 m 的大型户外迷宫场景中，并使用Direct Drive的Diablo机器人作为实验平台。系统能够快速成功地进行前端路径规划，并指导实时的后端优化，计算出考虑机器人非完整运动学的轨迹。Diablo机器人高效安全地导航通过迷宫，总位移约150米。前端模型部署在板载平台上的推理时间仅为25毫秒，并且即使面对之前未考虑的障碍物，机器人也能由于快速的后端优化而迅速避开。在资源受限的板载平台上，后端重新规划的平均时间约为40毫秒。

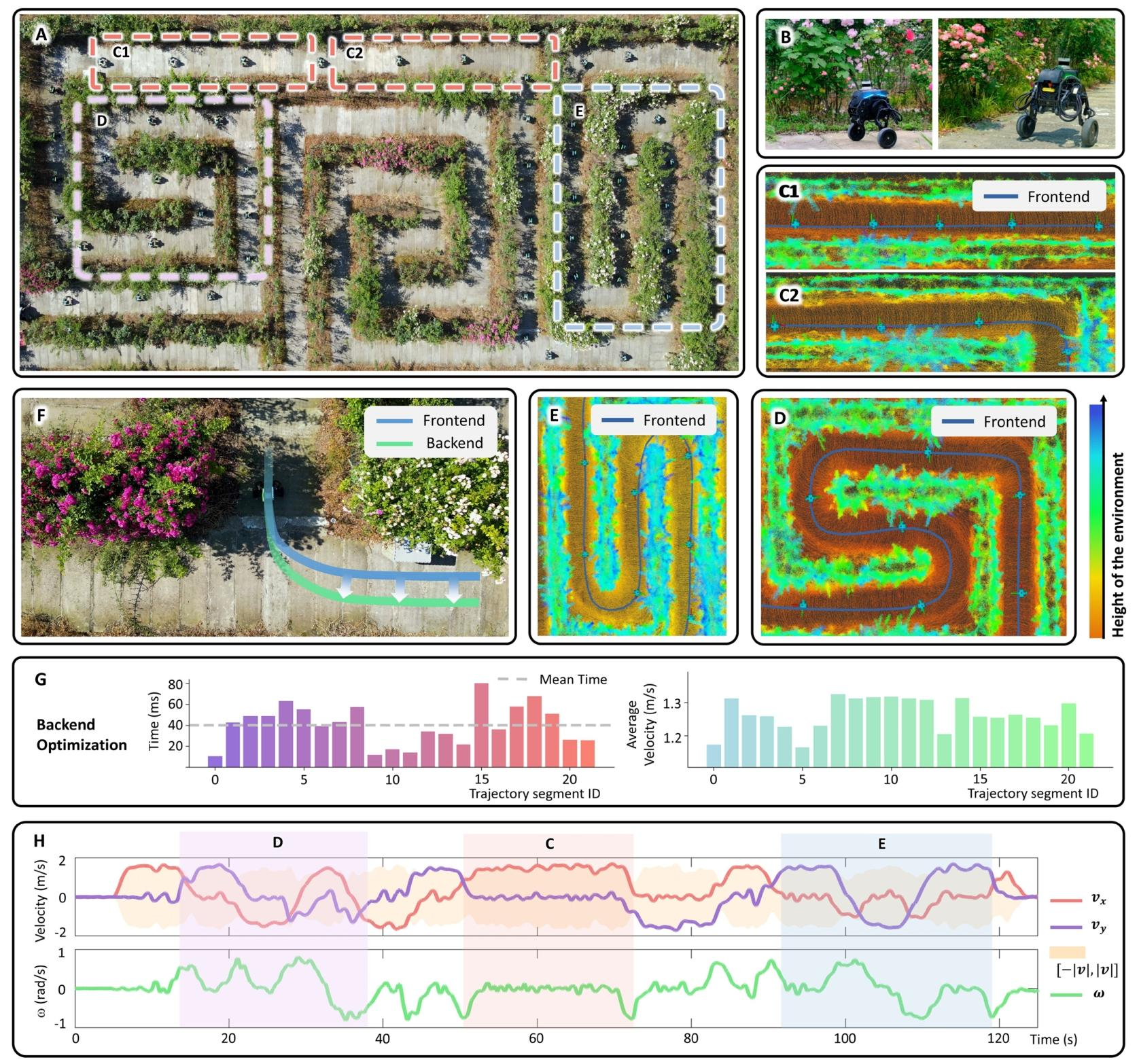
图5：大规模户外迷宫实验。（A）展示 Diablo 在复杂迷宫中导航的连续快照。（B）Diablo 的快照。（C）长直走廊。（D）横向蜿蜒的迷宫。（E）纵向蜿蜒的迷宫。（F）后端优化的示意图。（G）显示轨迹优化结果的条形图。（H）迷宫导航过程中机器人的状态。

这篇研究，为复杂环境下的机器人导航带来了“AI赋能的分层运动规划新范式”，展现了将人类直觉与数值优化深度融合的强大潜力。通过前端神经网络的快速路径生成，机器人能够像人类一样从宏观层面直观地感知并规划可行路径，有效规避了传统搜索算法在复杂场景下的效率瓶颈。而后端创新的双层多项式轨迹优化，则从根本上解决了微分平坦模型中困扰已久的奇点问题，确保了轨迹在各种复杂机动下的数值稳定性和高阶运动学可行性，显著提升了机器人轨迹的质量和可执行性。这一分层、稳定且高效的规划框架，不仅在模拟和真实世界的迷宫、固定翼导航等大规模实验中得到了验证，更为未来自动驾驶和自主机器人技术在真实、非结构化环境中的广泛部署铺平了道路，预示着机器人将能更智能、更安全地融入我们的生活。