前言
在自主移动机器人路径规划的学习与开发过程中,我接触到Time Elastic Band算法,并将该算法应用于实际机器人,用于机器人的局部路径规划。在此期间,我也阅读了部分论文、官方文档以及多位大佬的文章,在此对各位大佬的分享表示感谢。在本文中,我将分享Time Elastic Band算法的原理、个人对Time Elastic Band算法的理解以及在ROS下通过teb_local_planner对该算法进行演示和讲解。
01
相关论文
以下两篇论文主要介绍了Time Elastic Band算法以及使用稀疏模型进行优化:
[1].C. Rösmann, W. Feiten, T. Wösch, F. Hoffmann and T. Bertram: Trajectory modification considering dynamic constraints of autonomous robots. Proc. 7th German Conference on Robotics, Germany, Munich, 2012, pp 74–79.
[2].C. Rösmann, W. Feiten, T. Wösch, F. Hoffmann and T. Bertram: Efficient trajectory optimization using a sparse model. Proc. IEEE European Conference on Mobile Robots, Spain, Barcelona, 2013, pp. 138–143.
以下两篇论文介绍了同时规划多条轨迹,并选取出当前的全局最优轨迹:
[1].C. Rösmann, F. Hoffmann and T. Bertram: Integrated online trajectory planning and optimization in distinctive topologies, Robotics and Autonomous Systems, Vol. 88, 2017, pp. 142–153.
[2].C. Rösmann, F. Hoffmann and T. Bertram: Planning of Multiple Robot Trajectories in Distinctive Topologies, Proc. IEEE European Conference on Mobile Robots, UK, Lincoln, Sept. 2015.
以下这篇论文介绍了类汽车机器人的轨迹优化:
[1].C. Rösmann, F. Hoffmann and T. Bertram: Kinodynamic Trajectory Optimization and Control for Car-Like Robots, IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, Sept. 2017.
02
算法原理概述
本文依据Christoph Rösmann在论文中的描述,对eletic band进行定义:将给定的路径视为受内外力影响的弹性橡皮筋,使其变形,而内外力相互平衡,使路径收缩,同时与障碍物保持一定的距离,其中内外力就是对机器人运动的所有约束。而对于time eletic band,则在给定路径中间插入N个控制橡皮筋形状的控制点(机器人姿态),在点与点之间定义运动时间Time,即为Time Elastic Band算法。
通过上述定义我们可以看出,Time Elastic Band算法把路径规划问题描述为一个多目标优化问题,即对最小化轨迹执行时间、与障碍物保持一定距离并遵守运动动力学约束等目标进行优化。因为优化的大多数目标都是局部的,只与机器人的某几个连续的状态有关,所以该优化问题为对稀疏模型的优化。通过求解稀疏模型多目标优化问题,可以有效获得机器人的最佳运动轨迹。
求解稀疏模型多目标优化问题,可通过构建超图(hyper-graph),使用g2o(通用图优化)框架中关于大规模稀疏矩阵的优化算法来求解。机器人状态和时间间隔作为nodes,目标函数和约束函数作为edges,各nodes由edges连接构成hyper-graph。在该hyper-graph中,每个约束为一条edge,且每条edge允许连接的nodes的数目不受限制。
Time Elastic Band算法通俗的解释就是从给定路径中得到一系列带时间信息的离散位姿(pose),通过图优化的方法将这些离散位姿组成满足时间最短、距离最短和远离障碍物等目标的轨迹,同时满足机器人运动动力学的约束。需要注意的是,优化得到的轨迹并不一定满足所有约束,即给定的约束条件实际上都是软约束条件。
03
算法演示与讲解
通过阅读teb_local_planner的源码,我们可以知道teb_local_planner提供了许多参数和权重的配置接口,让用户可以为优化问题提供参数和权重,在不同的约束条件下指定优化目标。下面我们通过对teb_local_planner实现效果的简单演示来加深对Time Elastic Band算法的理解。
前面提到,Time Elastic Band算法可以在给定路径的基础上对轨迹进行优化,实现最小化轨迹时间、与障碍物保持距离等目标。
其中,与障碍物保持距离可以说是一个路径规划算法比较重要的功能,teb_local_planner提供了min_obstacle_dist和inflation_dist两个参数以及相应的权重,使用户可对轨迹与障碍物的距离进行调整,以此来满足不同环境下路径规划的需求。以下为配置不同参数值时,teb_local_planner规划出的不同的轨迹(为了使演示的效果更加明显,参数权重给得比较大):
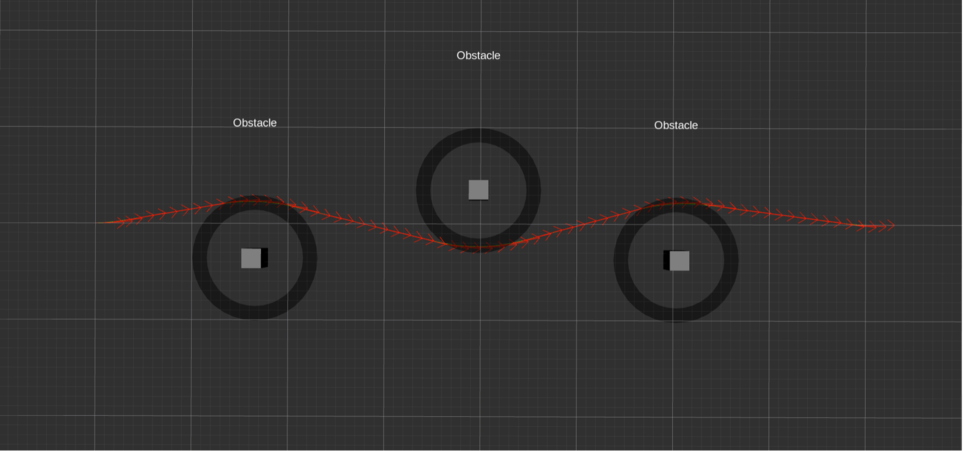
min_obstacle_dist为0.5,inflation_dist为0.6
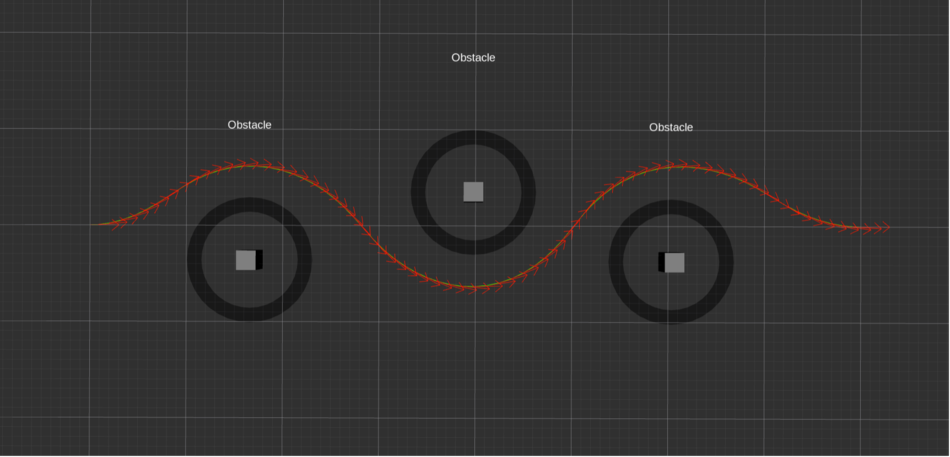
min_obstacle_dist为0.5,inflation_dist为1.0
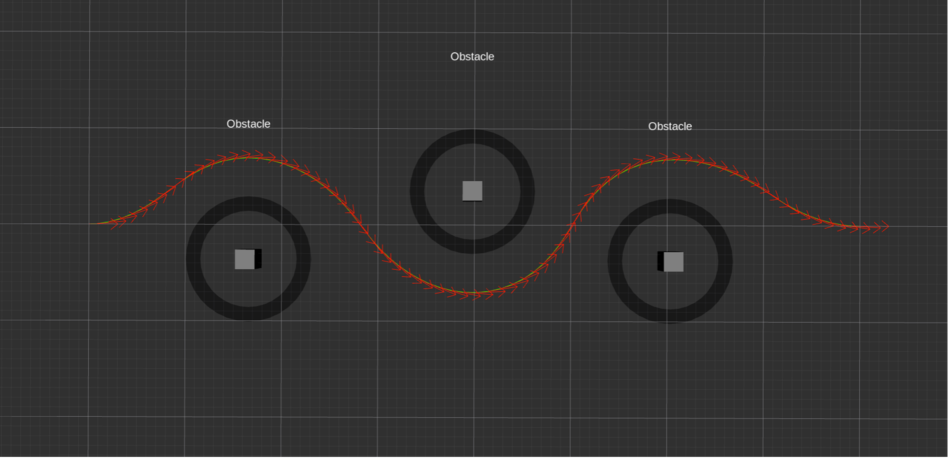
min_obstacle_dist为1.0,inflation_dist为0.6
通过以上效果可以看出,min_obstacle_dist和inflation_dist两个参数的值会导致teb_local_planner规划出不同的轨迹。min_obstacle_dist可以视为比inflation_dist更为严格的约束条件,只有当inflation_dist的值大于min_obstacle_dist时,inflation_dist才会影响teb_local_planner规划出的轨迹。
当然,参数对应权重的大小也会对规划出的轨迹有一定影响。在实际的应用过程中,需要用户对环境以及机器人自身的定位精度进行评估,从而设定合理的参数值,使得teb_local_planner能够规划出较优的路径。
除了与障碍物保持距离,如何合理并有效地跟随全局路径也是衡量一个局部规划算法好坏的重要标准。
teb_local_planner提供global_plan_viapoint_sep参数以及相应的权重,使用户可以根据不同的需求对期望轨迹设定约束条件。为了更好的理解该参数的作用,我首先解释一下viapoint,viapoint可以理解为通过点,即要求teb_local_planner规划出的轨迹必须通过某个点。下面通过一个极端一点的例子来看一下viapoint的效果:
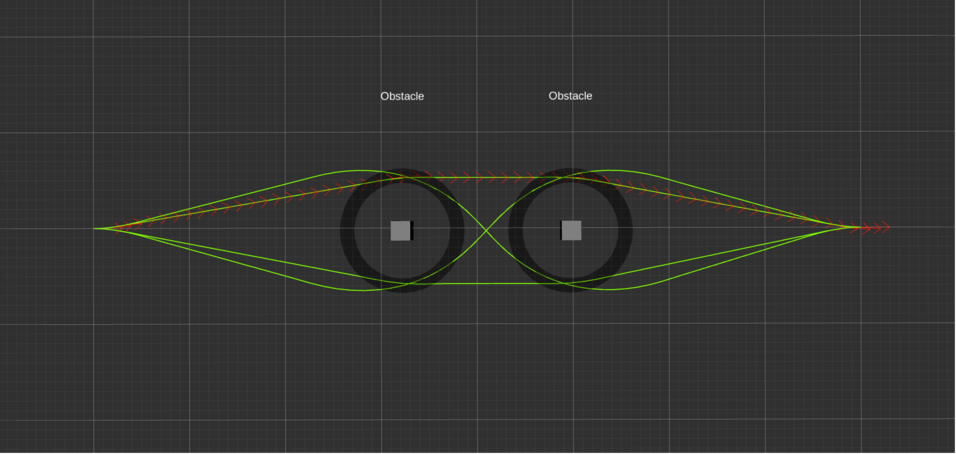
未设置viapoint
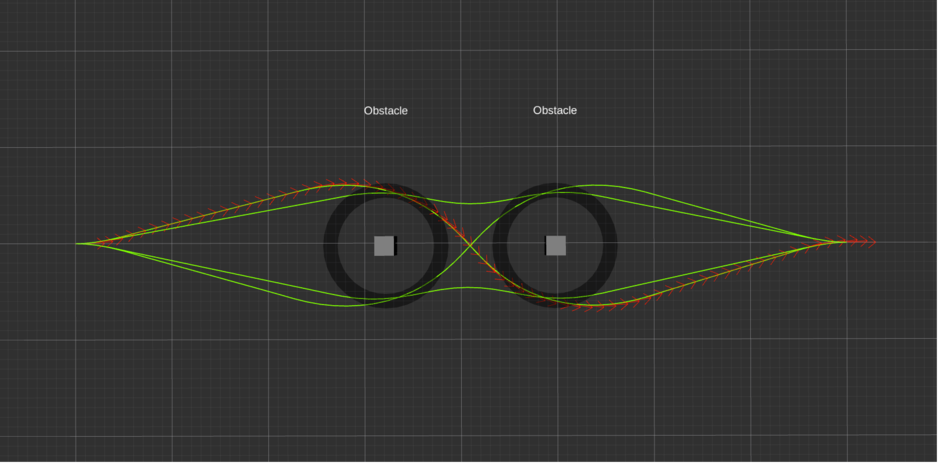
在两个障碍物中间设置了viapoint
可以看到,上面两幅图中,带红色箭头的轨迹为teb_local_planner规划出的轨迹。未设置viapoint时,teb_local_planner选取了上方的轨迹为最优轨迹,当在两个障碍物中间设置了viapoint,最优轨迹从两个障碍物中间穿过。由此可以看出,viapoint对teb_local_planner规划选取的最优轨迹有很大的影响。从侧面也反映出,Time Elastic Band算法是尽可能地满足设定的多个约束条件,选取出最优的轨迹。
现在,我们再来看global_plan_viapoint_sep在局部规划中的作用,该参数的描述为“从全局路径中选取的每两个连续通过点之间的最小间隔”,结合对viapoint的理解,从该描述中我们可以知道,该参数影响的是teb_local_planner规划的最优轨迹对全局路径的跟随效果。
当global_plan_viapoint_sep的值比较小时,从全局路径中选取的viapoint比较密集,最优轨迹对全局路径的跟随效果比较好;当global_plan_viapoint_sep的值比较大时,从全局路径中选取的viapoint比较稀疏,最优轨迹对全局路径的跟随效果比较差,但此时的最优轨迹可能更加平滑。
以下为使用Car-like模型时global_plan_viapoint_sep设置不同的值实现的路径规划的效果(同样的,为了使演示效果更加明显,适当地加大参数的权重):
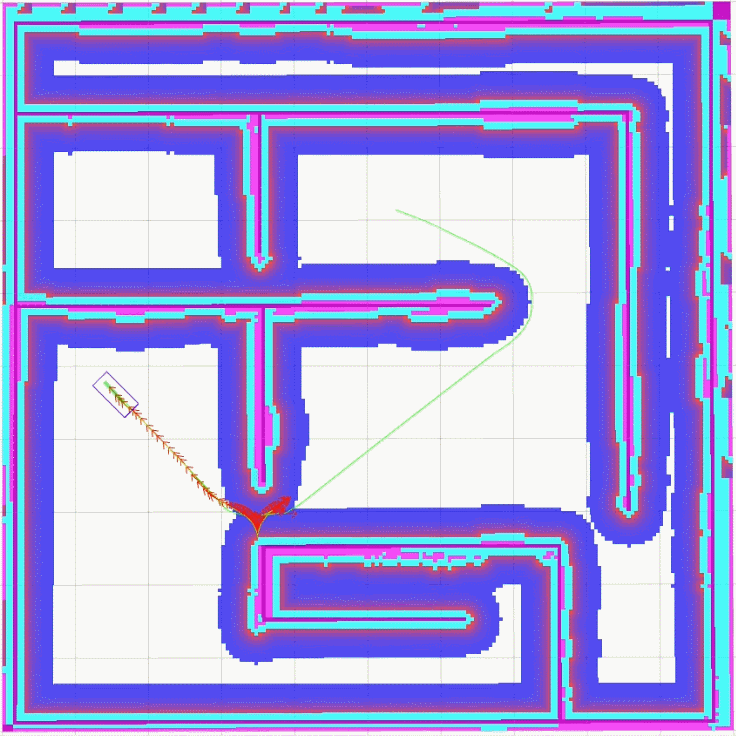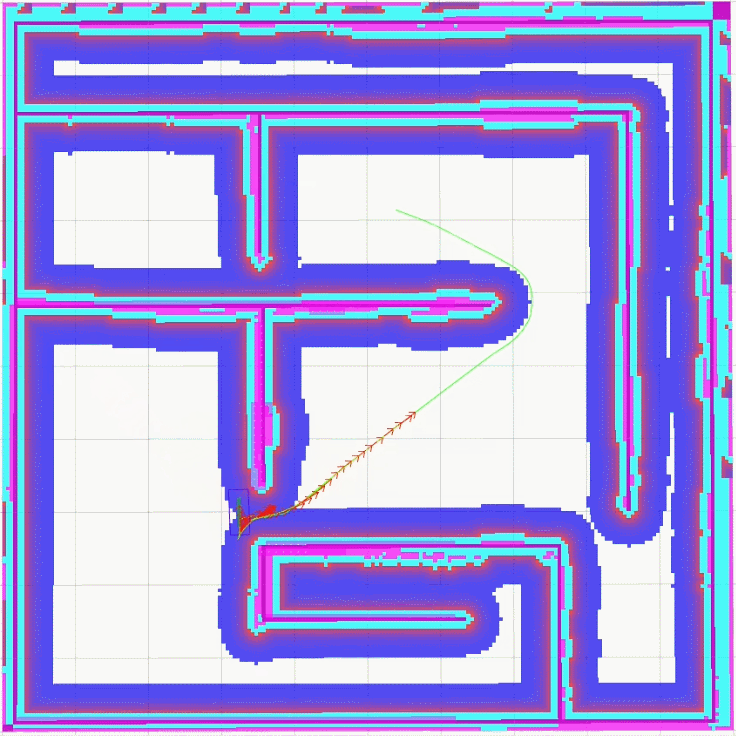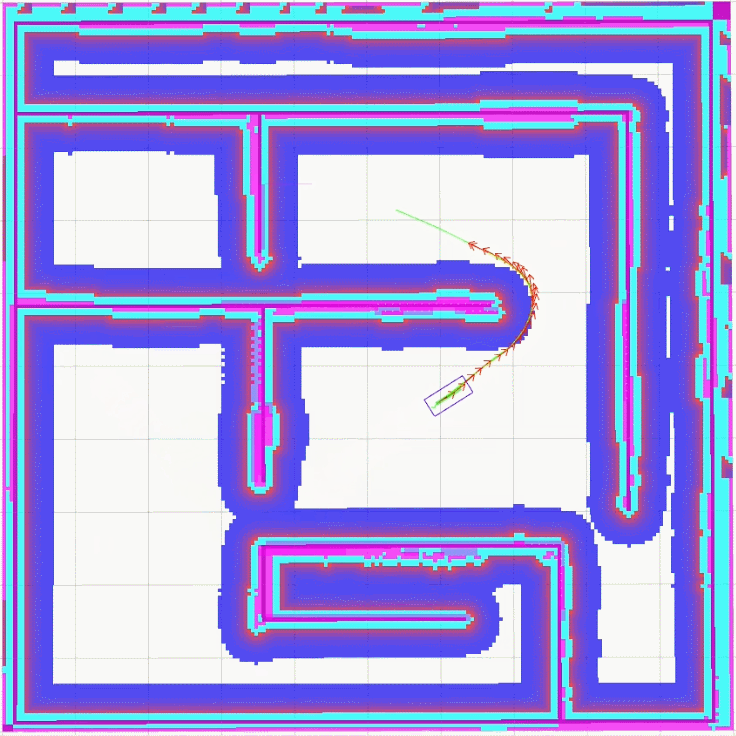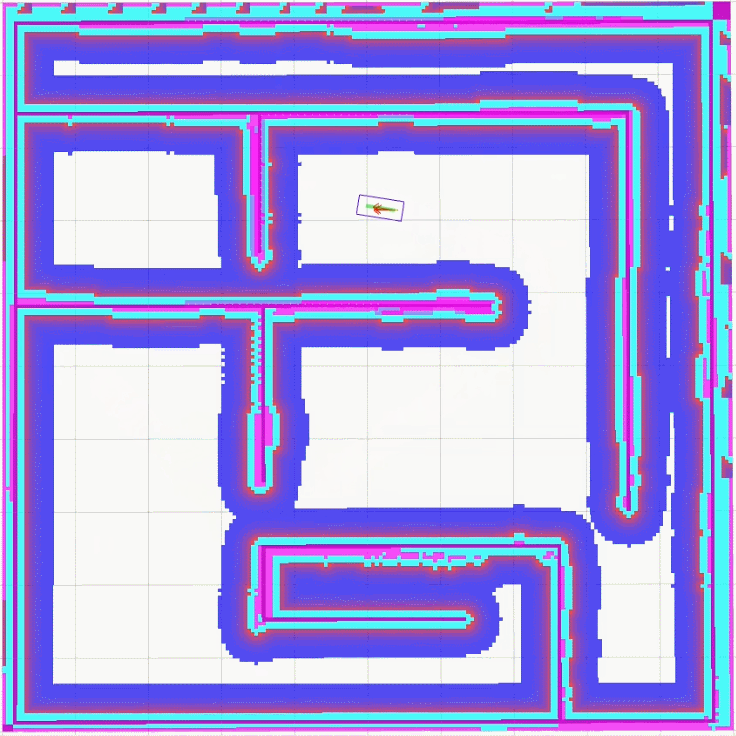
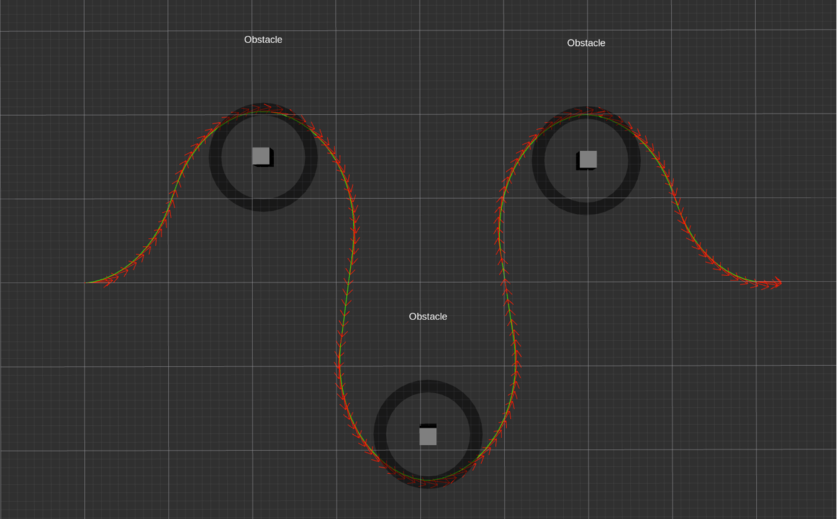
global_plan_viapoint_sep设置为0.1
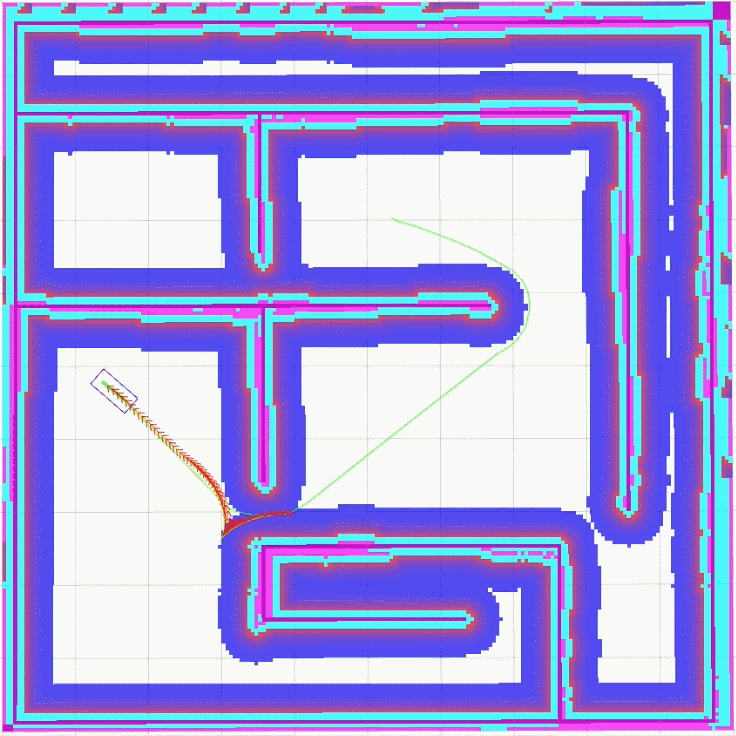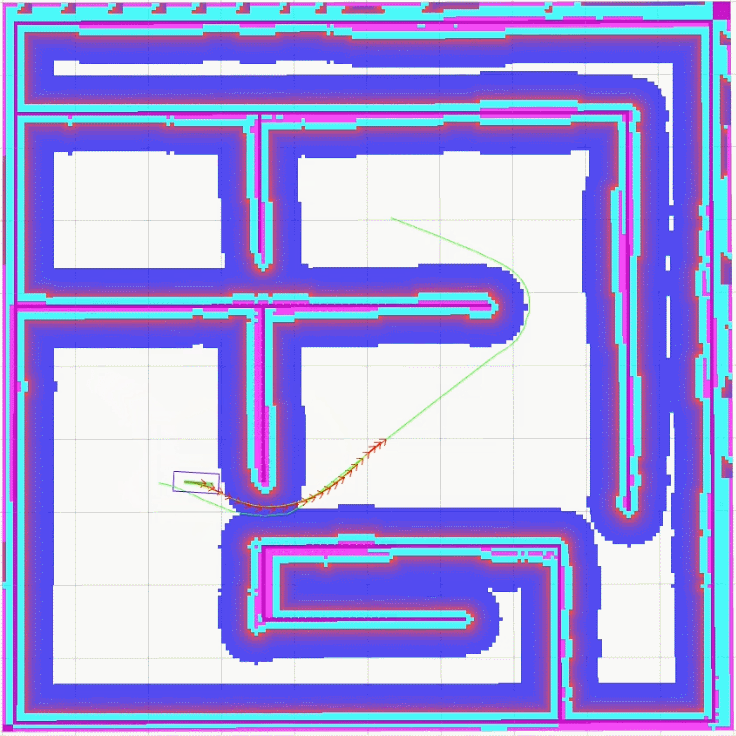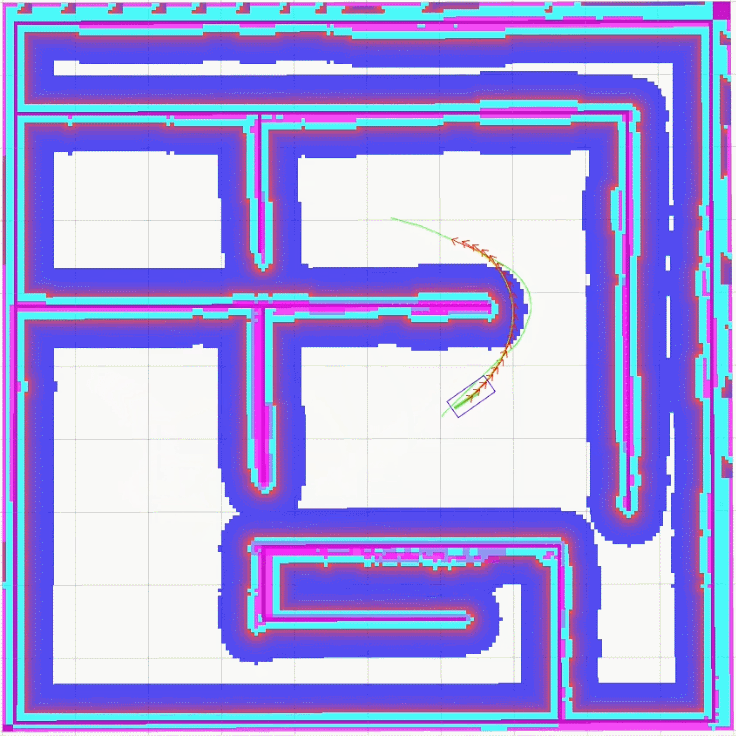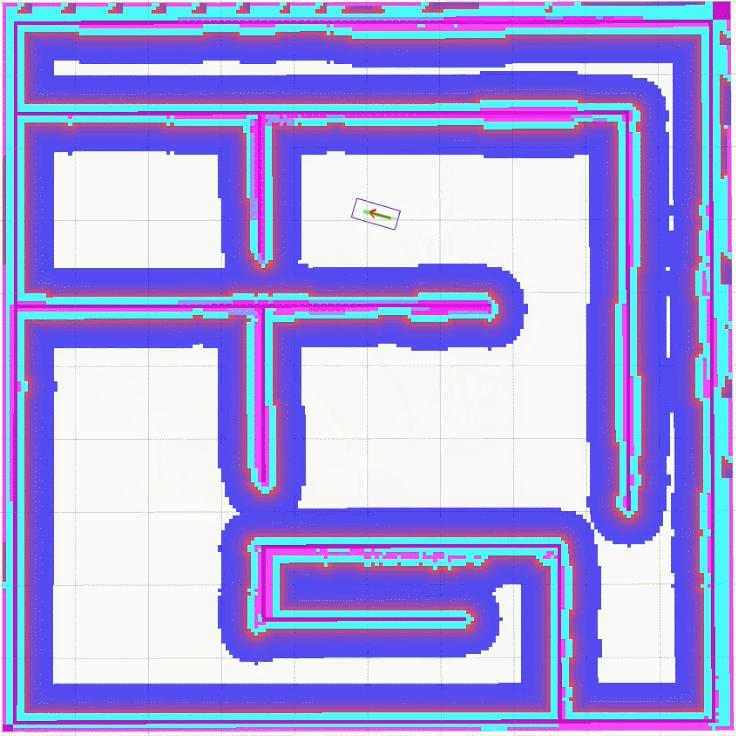
global_plan_viapoint_sep设置为5.0
从上面的实现效果可以明显看出, 当global_plan_viapoint_sep设置为0.1时,最优轨迹很紧密地跟随全局路径,Car-like模型在转向时需要多次调整角度,当global_plan_viapoint_sep设置为5.0时,最优轨迹并没有严格遵循全局路径,而是更为顺滑地完成转向。这是global_plan_viapoint_sep设置不同值时,teb_local_planner选取最优轨迹的不同效果。
在与障碍物保持距离和跟随全局路径的情况下,Time Elastic Band算法遵循运动动力学约束。teb_local_planner提供了max_vel_x和max_vel_theta等多个参数以及相应的权重,用户可根据实际机器人的性能进行设置。下面我们通过一个示例来简单看一下Time Elastic Band算法对速度约束的效果:
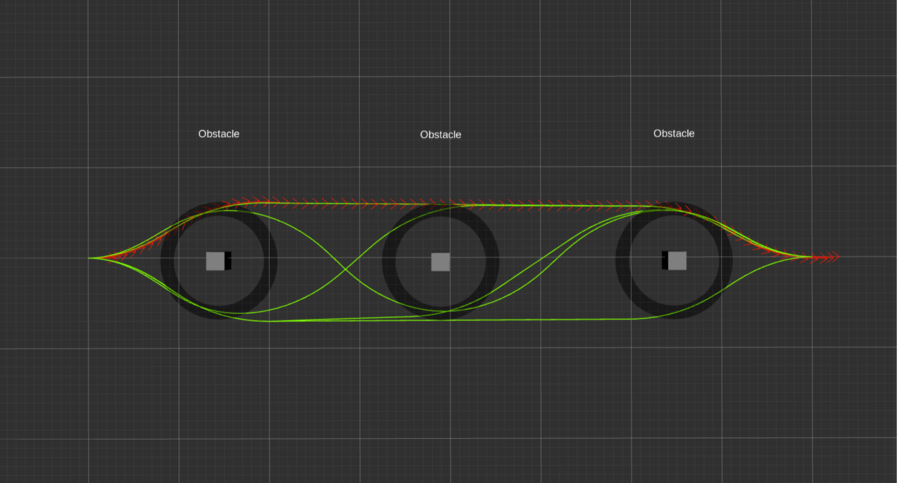
存在障碍物的情况下,teb_local_planner选取的最优轨迹
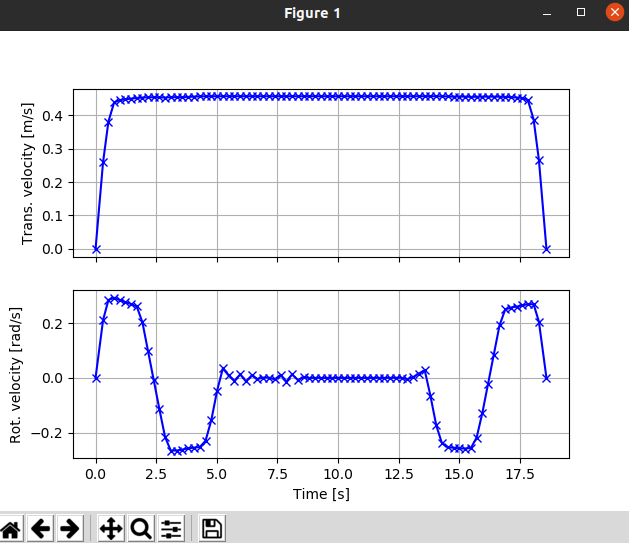
与上述轨迹对应的线速度和角速度曲线
max_vel_x为0.4m/s,max_vel_theta为0.3rad/s
我们可以发现,轨迹对应的线速度曲线的最大速度大于max_vel_x,这是因为max_vel_x对应的权重设置得较小导致的。由此也可以反映出Time Elastic Band算法遵循的约束条件为软约束,用户可以通过权重设定算法是否严格遵循约束条件。
说到这里,可能也有小伙伴发现了,在上面演示的过程中,teb_local_planner并不仅仅规划出一条路径,而是从多条路径中选取最优轨迹,这就不得不提到teb_local_planner中的Homotopy Class Planner,用户可以将enable_multithreading参数设置为True来开启同时规划多条路径,并从中选取最优轨迹。下面我们也来看一下只规划一条轨迹与同时规划多条路径并选取最优轨迹的对比:
只规划一条轨迹
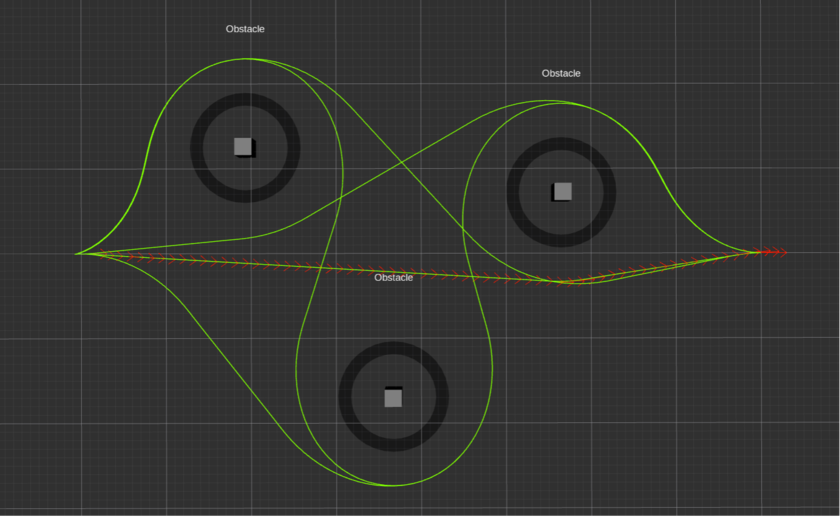
同时规划多条路径并选取最优轨迹
从上面的对比可以看出,在某些极端条件下,同时规划多条路径并选取最优轨迹得到的轨迹更符合全局最优,也更合理。当然,同时规划多条路径也将消耗更多的机器性能。在实际应用过程中,用户应当根据具体情况合理取舍。
04
总结
通过上面的介绍,可以看出Time Elastic Band算法有很多的优点,可以满足时间最短、距离最短和远离障碍物等目标以及满足机器人运动动力学的约束。那是不是Time Elastic Band算法就没有缺点呢?答案是否定的。
从前文我们可以知道,Time Elastic Band算法的大多数约束都是软约束条件。若参数和权重设置不合理或者环境过于苛刻,都有可能导致Time Elastic Band算法规划失败,出现非常奇怪的轨迹。因此,teb_local_planner中包含了检测冲突的部分,判断轨迹上的点是否与障碍物存在冲突,此时需要考虑机器人的实际轮廓。
在实际的开发过程中,更多地需要考虑机器人自身其他模块的性能,例如电机能够提供的最大加速度,定位算法的精度等,同时也要考虑具体的环境以及选择Time Elastic Band算法是否合理,如此才能将其性能发挥出更好的效果。
在本文中,我分享了我对Time Elastic Band算法的一点理解,但毕竟认知有限,对算法的部分内容的理解还是比较粗浅的,望大家多多包涵,有什么问题也希望能够与大家多交流。在后续的文章中,我会分享ROS自主移动机器人的开发以及各类算法的应用,有机会的话也会对Time Elastic Band算法的原理进行更加深入的解析,希望大家多多支持。
teb_local_planner github项目地址:
https://github.com/rst-tu-dortmund/teb_local_planner.git
在ROS noetic下安装teb_local_planner:
从ROS官方仓库中安装:
sudo apt install ros-noetic-teb-local-planner
从github仓库中下载源码进行编译:
git clone https://github.com/rst-tu-dortmund/teb_local_planner.git








 本文介绍了TimeElasticBand算法的原理,将其应用于ROS中的teb_local_planner进行机器人局部路径规划。通过多篇相关论文概述算法背景,并详细解释了算法如何通过图优化处理时间、距离和障碍物避障的多目标优化问题。此外,文章还展示了teb_local_planner的参数配置如何影响路径规划,包括与障碍物保持距离、跟随全局路径和运动动力学约束。最后,讨论了算法的优缺点以及实际应用中的考虑因素。
本文介绍了TimeElasticBand算法的原理,将其应用于ROS中的teb_local_planner进行机器人局部路径规划。通过多篇相关论文概述算法背景,并详细解释了算法如何通过图优化处理时间、距离和障碍物避障的多目标优化问题。此外,文章还展示了teb_local_planner的参数配置如何影响路径规划,包括与障碍物保持距离、跟随全局路径和运动动力学约束。最后,讨论了算法的优缺点以及实际应用中的考虑因素。
















 216
216

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








