题目传送门 \colorbox{orange}{\color{white}\texttt{题目传送门}} 题目传送门
不保证本篇题解不会被 hack
A*不加可和并堆优化也是可以水过的哦。
首先我们可以写一个不加任何剪枝与卡常的代码(为了缩短文章篇幅,只给出关键代码):
dij(n);//tmp[i] 表示 i 到 n 的最短路
pq<pair<double,int>>q;//pq是小根堆
q.push({tmp[1],1});
while(q.size()){
int u=q.top().second;
double t=q.top().first;
q.pop();
v[u]++;
if(t>e)continue;
if(u==n){
ans++;
e-=t;
continue;
}
for(auto[v,w]:g[u]){
q.push({t+w+tmp[v]-tmp[u],v});
}
}
然后你就会发现有两个点 MLE 了(#1 & #4),经过测试,dij 只使用了 11 11 11 MB,这也就意味着 A* 用了至少 117 117 117 MB,经过估算,队列中大约存储了 6.3 × 1 0 6 6.3\times10^6 6.3×106 个元素,显然,队列是使用空间最大的变量。
为了使队列元素个数变少,我们需要删除不必要的元素,也就是对队列长度进行限制。
当在判断元素 x x x 是否可以删除时,只要满足比队列中 x x x 大的树的和 s u m > E sum>E sum>E,那么 E E E 一定会在 x x x 出队之前就被减为负数,一定不会计算到 x x x 出队,所以这个时候 x x x 在不在队列里就不重要了。
也就是说,当队列中元素总和大于 E E E 时,可以将队列中最大的元素删掉。
具体来讲就是:
multiset<pair<double,int>>q;//注意这里为了删除最大元素将优先队列换成了 multiset
q.insert({tmp[1],1});
double sum=tmp[1];
while(!q.empty()){
int u=q.begin()->second;
double t=q.begin()->first;
q.erase(q.begin());
if(t>e)break;
sum-=t;
if(u==n){
ans++;
e-=t;
continue;
}
for(auto[v,w]:g[u]){
double tmp2=t+w+tmp[v]-tmp[u];
q.insert({tmp2,v});
sum+=tmp2;
if(sum>e){
auto tmp=q.end();tmp--;
sum-=tmp->first;
q.erase(tmp);//删除最大元素
}
}
}
这样,我们就限制了队列长度不会太大,于是我们解锁了新的测试信息:TLE(#1)。
由于我实在是太菜了,我下载了这个数据点,发现这个图的结构如下:
- n = 5000 n=5000 n=5000。
- 1 1 1 到 5000 5000 5000 有一条单向边。
- 1 1 1 到 i ( i ∈ Z ∩ [ 2 , n − 1 ] ) i(i\in\Z\cap[2,n-1]) i(i∈Z∩[2,n−1]) 有一条双向边。
- E = 10000000 E=10000000 E=10000000
不难发现,对于编号在 2 2 2 到 n − 1 n-1 n−1 之间的点,似乎这些点好像可以合并成一个点,如果这样的话那就只剩下 3 3 3 个点了,不管你怎么搜都不会超时。
我们必须分析清楚,什么时候可以合并两个点。
我画了如下一个抽象的图来解释:
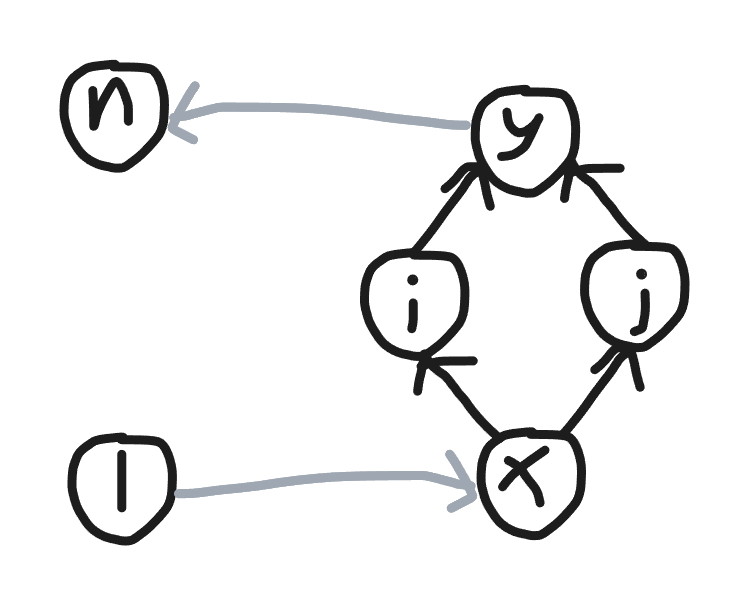
这个图表述的含义是:
- 有 1 1 1 到 x x x 的路径
- 连向点 i , j i,j i,j 的只有 x x x,且 x x x 到 i i i 的边权等于到 j j j 的。
- i , j i,j i,j 只连向 y y y,且 i i i 到 y y y 的边权等于 j j j 到 y y y 的。
- 有 y y y 到 n n n 的路径
如果满足这些条件,那么 i i i 和 j j j 就可以看做是同一个点,显然可以合并,减少计算量。
合并部分的代码:
for(int i=2;i<n;i++){
if(gt(i)!=i)continue;
for(int j=i+1;j<n;j++){//n^2 不会 TLE,所以直接无脑暴力
if(gt(j)!=j)continue;//gt 是并查集找祖先的函数
if(g[i].size()==1&&g2[i].size()==1&&g[i]==g[j]&&g2[i]==g2[j]){//g2 是反图
merge(i,j);//并查集合并
}
}
}
for(int i=1;i<=n;i++){
if(f[i]==i){
cnt[i]=sz[i];//sz[i] 是联通块大小,cnt 表示这个点是多少个点1合并得到的
}
}
合并之后,只需要把
u
u
u 更新一次到
v
v
v 变为更新 cnt[v] 次到
v
v
v 就可以了,但是(可能)会 TLE,所以考虑只在队列中插入一次
v
v
v,但是记录这个
v
v
v 相当于插入了 cnt[v] 次。
具体看代码(这个剪枝可能有一点点小问题,因为几乎只有 #1 用了这个剪枝):
#include<bits/stdc++.h>
using namespace std;
template<typename T>
using pq=priority_queue<T,vector<T>,greater<T>>;
int n,m,v[5005],ans,cnt[5005];
double tmp[5005],e;
vector<pair<int,double>>g[5005],g2[5005];
void dij(int x){
for(int i=1;i<=n;i++)tmp[i]=1e18;
tmp[x]=0;
pq<pair<double,int>>q;
q.push({0,x});
while(q.size()){
int u=q.top().second;
double t=q.top().first;
q.pop();
if(v[u])continue;
v[u]=1;
for(auto[v,w]:g2[u]){
if(tmp[v]>t+w){
tmp[v]=t+w;
q.push({tmp[v],v});
}
}
}
}
namespace aaaa{
int f[5005],n,sz[5005];
void init(){
n=::n;
for(int i=1;i<=n;i++)f[i]=i,sz[i]=1;
}
int gt(int x){if(x==f[x])return f[x];return f[x]=gt(f[x]);}
void merge(int x,int y){
f[x]=y;
sz[y]+=sz[x];
sz[x]=0;
}
}
signed main(){
// freopen("P2483_1.in","r",stdin);
cin>>n>>m>>e;
aaaa::init();
while(m--){
int u,v;
double w;
cin>>u>>v>>w;
g[u].push_back({v,w});
g2[v].push_back({u,w});
}
dij(n);
for(int i=2;i<n;i++){
if(aaaa::gt(i)!=i)continue;
for(int j=i+1;j<n;j++){
if(aaaa::gt(j)!=j)continue;
if(g[i].size()==1&&g2[i].size()==1&&g[i]==g[j]&&g2[i]==g2[j]){
aaaa::merge(i,j);
}
}
}
for(int i=1;i<=n;i++){
if(aaaa::f[i]==i){
cnt[i]=aaaa::sz[i];
}
}
multiset<pair<double,pair<int,int>>>q;
q.insert({tmp[1],{1,cnt[1]}});
double sum=tmp[1];
while(!q.empty()){
pair<double,pair<int,int>>p=*q.begin();
int u=p.second.first;
int times=p.second.second;
double t=p.first;
q.erase(q.begin());
if(t>e)break;
sum-=t*times;
if(u==n){
ans+=min<int>(times,e/t);
e-=t*times;
e=max<double>(e,0);
continue;
}
for(auto[v,w]:g[u]){
if(cnt[v]==0)continue;
double tmp2=t+w+tmp[v]-tmp[u];
if(tmp2>e)continue;
q.insert({tmp2,{v,times*cnt[v]}});
sum+=tmp2*times*cnt[v];
if(sum>e){
auto tmp=q.end();tmp--;
pair<double,pair<int,int>>p=*tmp;
int t=p.second.second;
double x=p.first;
int u=p.second.first;
sum-=x*t;
q.erase(tmp);
int k=(e-sum)/x;
if(k)q.insert({x,{u,k}}),sum+=k*x;
}//注意这一部分常数稍微大一点就会 TLE 80 分,因为进行了大量的乘除运算
}
}
cout<<ans;
return 0;
}
最后是跑了 1.97 1.97 1.97 秒,空间用了 15.85 15.85 15.85 MB。
终于,我们成功的让代码长度多了一倍。
注意到我并没有特判。
如果你认为我在特判,那么我们可以加强一下这个剪枝。
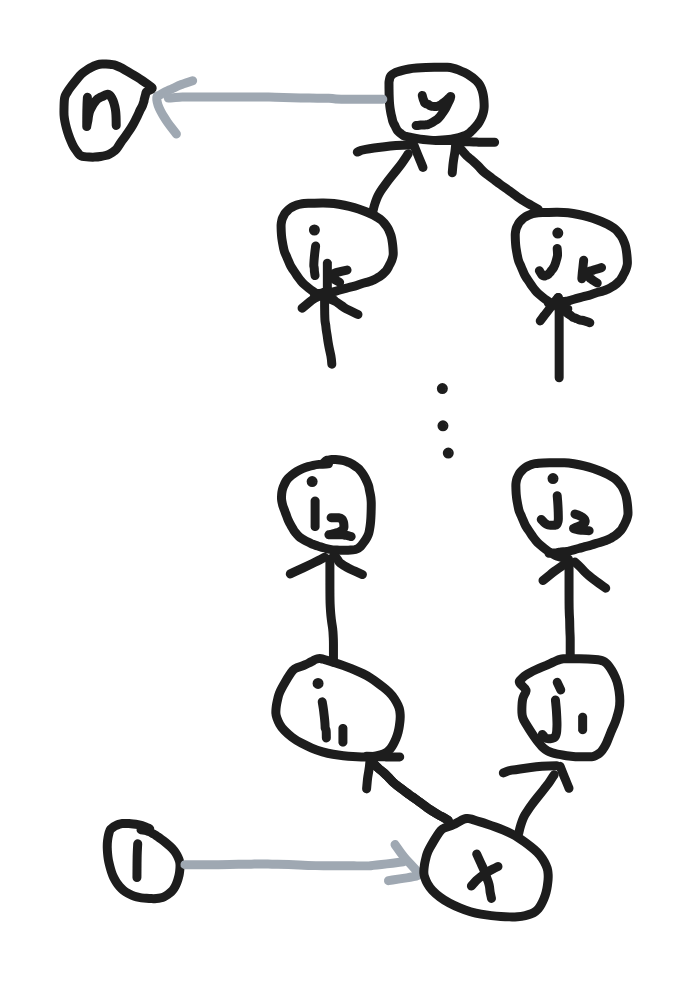
如果是这种情况,那么 ( i 1 , j 1 ) (i_1,j_1) (i1,j1), ( i 2 , j 2 ) ⋯ ( i k , j k ) (i_2,j_2)\cdots(i_k,j_k) (i2,j2)⋯(ik,jk),均可以合并。
判断也很好做,先确定 x x x,再从 x x x 的出边开始 dfs,只要出度为 1 1 1 就继续搜,最终搜到 y y y,判断两条路劲对应边权是否相等即可。
还有个优化:如果 multiset 中有元素
{
i
,
j
,
k
}
\{i,j,k\}
{i,j,k} 和
{
i
,
j
,
m
}
\{i,j,m\}
{i,j,m} 那么我们可以合并为
{
i
,
j
,
k
+
m
}
\{i,j,k+m\}
{i,j,k+m}。
只需要判断插入的位置前一个和后一个是否可以合并就可以了。





















 2125
2125










