算法笔记(一)归一化之BN LN IN

最新推荐文章于 2025-09-11 15:32:06 发布
原创 最新推荐文章于 2025-09-11 15:32:06 发布 · 868 阅读 · 8 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #深度学习 #神经网络

本文详细介绍了深度学习中常用的几种归一化技术，包括BatchNormalization (BN)、LayerNormalization (LN)、InstanceNormalization (IN)、GroupNormalization (GN)、SwitchableNormalization (SN)和WeightNormalization (WN)。BN通过缓解Internal Covariate Shift加速训练，而LN、IN、GN和WN各有适用场景，如LN适合RNN，IN适用于风格迁移，GN解决小batch问题，SN自动选择合适归一化，WN则在权值维度上进行归一化。各种归一化技术有其优缺点，选择需根据具体任务和网络结构来定。

前言

  • 数据规一化的作用:
    • 调整数据分布,增加网络泛化度.
    • 若每批数据分布不同,神经网络需要不断调整模型权重去适应不同的数据分布,因此可以增加训练速度.即缓解Internal Covariate Shift问题,将数据分布拉到激活函数的非饱和区,具有权重/数据伸缩不变性的特点.
    • 起到缓解梯度消失/爆炸,加速训练,正则化的效果.
  • 内部协方差转移internal convarite shift:
    • 简设模型函数 y=f(θ,x)y=f(\theta,x)y=f(θ,x),训练时,每层网络的输入数据分布会不断变化,导致参数θ\thetaθ变化和y变化.
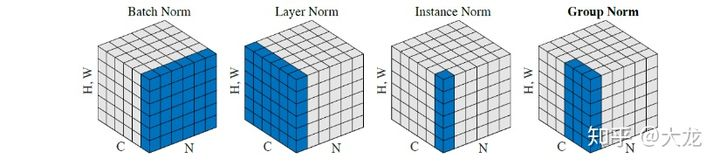
  • 处理维度(B,C,H,W)数据时,
    • BN:在batch上,对(C,H,W)做归一化.
    • LN:在Channel上,对(B,H,W)做归一化.
    • GN:在Channel上对C分组,即对(G,H,W)做归一化,其中G*K=C,将K个GN结果合并为最终归一化结果.
    • IN:在图像像素上,对(H,W)做归一化.
    • SN:是将BN LN IN结合,赋予不同权重,让网络自己去学习归一化层应该使用什么方法.
    • WN:对模型权重进行归一化.
      在这里插入图片描述
      在这里插入图片描述

1.Batch Normalization(BN)

过程

  1. 预处理:
    x(k)=x(k)−E[x(k)]Var[x(k)]x^{(k)}=\frac{x^{(k)}-E[x^{(k)}]}{Var[x^{(k)}]}x(k)=Var[x(k)]x(k)−E[x(k)]​
  2. 变换重构:
    x(k)=γ(k)x(k)+β(k)x^{(k)}=\gamma^{(k)}x^{(k)}+\beta^{(k)}x(k)=γ(k)x(
最低0.47元/天 解锁文章
深度学习笔记——归一化、正则化
haopinglianlian的博客
11-21 3087
本笔记介绍深度学习中常见的归一化、正则化。
归一化技术：从BatchNorm到RMSNorm——深度学习的稳定之锚
qq_43664407的博客
05-31 1287
​归一化技术已从辅助优化手段演变为深度学习的​​架构支柱​。
BN与LN归一化
M_arshal_的博客
10-25 326
d：特征 b：batch_size将多少数据打包 len：长度 BN就是取出一个特征（所有样本的一个特征），对其进行归一化，直到取完全部特征。 LN就是取出所有的batch，取出每个batch中的一个样本进行归一化。 ...
深度学习笔记-----归一化方法BN
YOULANSHENGMENG的博客
10-13 2804
1.什么是归一化：归一化又称规范化，并不是一个完全定义好的数学操作，通常是指将数据进行偏移和尺度缩放。是数据预处理中常用的手段。一般是将输入的数据约束固定到一定的范围如【0,1】。没有固定的数学表达式，根据需求定义将数据规定到一定范围内的数学表达式； 2.归一化方法的目的：实际上是通过采取不同的变换方式使各层的的输入数据近似满足独立的分布条件，并将各层的输出限定在一定的范围 3.在深度学习中常用的归一化方法：零均值归一化，也称为标准化方法，它用每一个变量值与其平均值之差除以该变量的标准差。经过这样的处.
BN（Batch Normalization）：批量归一化
studyeboy的专栏
06-24 3902
[paper]DeepLab2: A TensorFlow Library for Deep Labeling [code]DeepLab2: A TensorFLow Library for Deep Labeling DeepLab2 是一个用于深度标注的 TensorFlow 库，旨在为密集像素标注任务提供统一的、最先进的 TensorFlow 代码库，包括但不限于语义分割、实例分割、全景分割、深度估计，甚至 视频全景分割。 深度标记是指通过深度神经网络为图像中的每个像素分配预测值来解决计算机视觉问题
归一化总结：BN、LN、IN、GN、SN
weixin_47748259的博客
03-28 4593
在机器学习领域中，不同评价指标（即一组特征中的不同特征就是所述的不同评价指标）往往具有不同的量纲和量纲单位，这样的情况会影响到数据分析的结果，为了消除指标之间的量纲影响，需要进行数据标准化处理，以解决数据指标之间的可比性。即，原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。数据归一化一般有[0,1]归一化和正态分布归一化两种方法：[0,1]归一化：使结果值映射到[0，1]之间。
归一化方法：BN/LN/IN/GN/FN
热门推荐
Man
04-23 2万+
一、批量标准化(BN，Batch Normalization) 1、BN 简介 a、协变量偏移问题 我们知道，在统计机器学习中算法中，一个常见的问题是协变量偏移(Covariate Shift)，协变量可以看作是输入变量。一般的深度神经网络都要求输入变量在训练数据和测试数据上的分布是相似的，这是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。 传统的深度神经网络在训练...
Pytorch：正则化（L1、L2、Dropout）与归一化（BN、LN、IN、GN）
weixin_47255403的博客
12-10 2050
这次内容首先是正则化，正则化是一种缓解模型的过拟合问题的策略，我们学习了L2正则的原理，L1正则和L2正则的区别，然后学习了L2正则等价于权重衰减。 然后又学习了Dropout正则化，并且对比了一下L2正则和Dropout正则的效果。 第二部分是标准化，这主要是解决网络层输出的数据尺度变化不一致的问题， 首先学习了Batch Normalization，学习了它的原理和具体的使用方法，然后又介绍了其他三种标准化方法， LayerNorm Normalization、Instance Normalizati
【深度学习基础】归一化，白化，
Jiangnan_Cai的博客
10-30 453
当然，除了对图像的像素值进行归一化，在目标检测的 YOLO 家族中，我们也会对目标框的坐标和宽高进行归一化处理。归一化后数值落在哪个区间对后续的训练有什么影响呢？但是上面有几个答案都提到了归一化到。是一种更为推荐的归一化方式。
BN(Batch Normalization 批量归一化）
laozaoxiaowanzi的博客
07-31 4240
BN(Batch Normalization 批量归一化） BN（批量归一化）算法在DL中出现的频率很高，因为对于提升模型收敛速度来说具有非常好的效果。 本文将通过以下三个点来理解Batch Normalization。 一、什么是BN 我们在训练模型的时候希望训练集训练出来的模型在通过测试集时能够拥有和训练时一样的效果，为此，有这样一个假设，即训练集数据和测试集数据是满足相同分布的，这个叫做IID（独立同分布假设），就是随机变量相互独立互不影响且具有相同的分布形状和相同的分布参数，也就是训练...
各种归一化Normalization（BN、LN、IN、GN、WN）
Drug discovery
03-25 1万+
一. 本文的内容包括： 1.Batch Normalization，其论文：https://arxiv.org/pdf/1502.03167.pdf 2.Layer Normalizaiton，其论文：https://arxiv.org/pdf/1607.06450v1.pdf 3.Instance Normalization，其论文：https://arxiv.org/pdf/1607.08022.pdf 4.Group Normalization，其论文：...
动手学深度学习（二十三）——批量归一化（BN）
Liu Feng's Blog
08-14 4900
1. 批量归一化   现在的神经网络通常都特别深，在输出层向输入层传播导数的过程中，梯度很容易被激活函数或是权重以指数级的规模缩小或放大，从而产生“梯度消失”或“梯度爆炸”的现象，造成训练速度下降和效果不理想。   第二个是在深度神经网络之中损失都是再最后面，后面的层训练较快（梯度大），但是向后传播的最后的数据处其梯度很小，也就是说后面的层训较慢，而底层的变化会导致全部层的变化，也就致使靠近loss函数的顶部需要多次学习，导致收敛很慢   如何避免或者减轻这一现象的发生呢？归一化就是方法的一种。归一化将网
深度学习归一化方法总结(BN、LN、IN、GN)
weixin_43570470的博客
04-09 8410
一般在神经网络中会用到数据的归一化，比如在卷积层后进行归一化然后再下采样然后再激活等。目前比较受欢迎的数据归一化层有：BN(Batch Normalization)，LN(Layer Normalization)，IN(Instance Normalization)，GN(Group Normalization)这4种。本篇文章主要是对比一下它们各自是怎么计算的。 先看对数据的归一化是这么操作的。其实就是先计算均值和方差然后再标准化即可。具体的对一个标量数据，在给定的数据集中进行标准化是按如下进行计算的：
BN,LN,IN,GN的理解和用法
qq_44091004的博客
03-11 4276
BN,LN,IN,GN的理解和使用
深度学习基础之批量归一化（BN）
记录和分享
04-17 2360
BN工作原理解析
归一化操作LN
fht3873的博客
02-21 298
对一批图片按照单图片单通道进行处理，示例 公式：
一文详解BN（Batch Normalization，批量归一化）
最新发布
weixin_41413777的博客
09-11 1985
在深度学习中，BN（Batch Normalization，批量归一化） 是一种核心的优化技术，由 Google 团队在 2015 年的论文《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》中提出。其核心目标是解决 “内部协变量偏移（Internal Covariate Shift, ICS）” 问题，从而加速模型训练、提升训练稳定性，并允许使用更高的学习率。
四图秒懂BN、LN和IN
weixin_42078618的博客
06-01 8893
DL常见的三大网络类型，CNN、RNN和GAN，CNN用于CV领域较多，RNN则用于NLP方向较多，GAN就比较特殊，娱乐向的CV。而其中，最常用、最高效的三个技术点就是BN、LN和IN了，他们是三种网络的典型代表作。 1、BN（BatchNormalization） 看图说话。 我们假设有一批图像的feature maps传入网络中（如上）。其中，N表示batch_size，9*...
BN批量归一化操作
TranSad的博客
03-04 4203
BN（Batch-Normal）批量归一化是一个非常常见的步骤了，很多卷积神经网络都使用了批量归一化。 先回顾一下传统的的神经网络前向传播的过程，之前在这篇文章里详细描述过全连接神经网络的输入输出尺寸变化。 通过这个基础铺垫我们知道，对于神经网络中的一层，每输入一条数据 可以得到一条结果, 而实际上我们训练的时候大多数使用mini-batch，也就是一个batch一个batch地训练，所以数据会有多条，此时对于神经网络中的某一层，输入数据为， 输出数据为。 其中x[1]就...
简单描述BN LN等归一化方式
06-03
### Batch Normalization (BN) 和 Layer Normalization (LN) 的原理与比较 #### Batch Normalization (BN) Batch Normalization 是一种用于加速深度神经网络训练的技术，通过在每一层输入进行标准化处理来稳定学习过程。其核心思想是减少内部协变量偏移（Internal Covariate Shift），即随着网络参数的更新，中间层的分布会发生变化[^3]。具体来说，BN 对一个 mini-batch 内的所有样本在同一通道上的激活值进行归一化，使其均值接近 0，方差接近 1。这种归一化方式依赖于 batch size，并且需要计算整个 mini-batch 的均值和方差。 BN 的主要步骤包括： 1. 计算 mini-batch 内所有样本在同一通道上的均值和方差。 2. 使用这些统计量对每个样本的激活值进行归一化。 3. 引入可学习参数 γ 和 β 来恢复网络表达能力，允许模型调整归一化后的输出[^5]。 #### Layer Normalization (LN) Layer Normalization 是另一种归一化方法，特别适用于序列建模任务（如 RNN、Transformer）。与 BN 不同，LN 对每个样本自身的所有特征维度进行归一化，而不是跨样本计算均值和方差[^4]。因此，LN 不依赖于 batch size，适合小批量或单样本场景。 LN 的主要步骤为： 1. 对每个样本的所有特征维度计算均值和方差。 2. 使用这些统计量对该样本的激活值进行归一化。 3. 同样引入可学习参数 γ 和 β 来调整归一化后的输出[^4]。 #### BN 和 LN 的区别 | 特性 | Batch Normalization (BN) | Layer Normalization (LN) | |---------------------|-------------------------------------------------------------------------------------------------------------|-----------------------------------------------------------------------------------------| | 归一化范围 | 跨样本（mini-batch 内的所有样本） | 单样本（每个样本自身的所有特征维度） | | 是否依赖 batch size | 是，batch size 过小时效果可能不佳 | 否，适用于任意 batch size | | 适用场景 | 图像任务，尤其是卷积神经网络 | 序列任务，如 RNN、Transformer | | 统计量计算 | 基于 mini-batch 的均值和方差 | 基于单个样本的均值和方差 | #### 其他归一化方法 除了 BN 和 LN，还有其他归一化技术，例如 Instance Normalization (IN) 和 Group Normalization (GN)。 - **Instance Normalization (IN)**：对每个样本的每个通道独立进行归一化，类似于 LN，但仅作用于单个通道。IN 在生成对抗网络（GAN）中表现良好[^4]。 - **Group Normalization (GN)**：将通道分组并对每组进行归一化，结合了 BN 和 LN 的优点，不依赖 batch size 且适用于不同任务[^3]。 ```python import torch import torch.nn as nn # Batch Normalization 示例 bn = nn.BatchNorm2d(64) x = torch.randn(16, 64, 32, 32) # 输入形状 [batch_size, channels, height, width] y_bn = bn(x) # Layer Normalization 示例 ln = nn.LayerNorm([64, 32, 32]) y_ln = ln(x) # Group Normalization 示例 gn = nn.GroupNorm(num_groups=8, num_channels=64) y_gn = gn(x) ```
评论 1
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

nooobme

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值