(更新中)(手撕LLaMA-小白友好的论文解读)LLaMA：开放且高效的基础语言模型

LLaMA：开放且高效的基础语言模型

摘要

我们推出LLaMA，一系列参数规模从7B到65B不等的基础语言模型。我们在数万亿tokens上训练这些模型，并证明可以完全使用公开可获取的数据集训练最先进的模型，而无需依赖专有和不可访问的数据集。特别是，LLaMA-13B在大多数基准测试中超过了GPT-3（175B），而LLaMA-65B则与最佳模型Chinchilla-70B和PaLM-540B相比具有竞争力。我们向研究社区发布我们的所有模型¹。

[!NOTE]

就是用开源数据练了一个很厉害的大模型

1 引言

在海量文本语料库上训练的大型语言模型（LLMs）已经展示了其从文本指令或少量样例中执行新任务的能力（Brown等，2020）。这些少样本特性最初是在模型扩展到足够规模时出现的（Kaplan等，2020），由此产生了一系列专注于进一步扩展这些模型的工作（Chowdhery等，2022；Rae等，2021）。这些努力基于以下假设：更多的参数将带来更好的性能。然而，Hoffmann等人（2022）的最新研究表明，对于给定的计算预算，最佳性能并非由最大的模型实现，而是由在更多数据上训练的较小模型实现。

[!NOTE]

固定计算预算指的是在训练大型语言模型时分配的总计算资源限制。这些资源通常以FLOP(浮点运算次数)、GPU小时或能源消耗来衡量。你可以选择训练参数更多的大模型但使用较少数据或者训练参数较少的小模型但使用更多数据。相关研究表示相同的计算资源投入，选择较小模型+更多数据往往能获得更好的性能。这打破了之前认为"更大的模型总是更好"的假设。

Hoffmann等人（2022）的缩放法则的目标是确定如何为特定训练计算预算最佳地扩展数据集和模型规模。然而，这个目标忽视了推理预算，而推理预算在大规模部署语言模型时变得至关重要。在此背景下，给定目标性能水平，首选的模型不是训练最快的，而是推理最快的，尽管训练大型模型以达到某一性能水平可能成本更低，但训练时间更长的较小模型在推理阶段最终成本会更低。例如，虽然Hoffmann等人（2022）建议在200B tokens上训练10B参数的模型，但我们发现即使在1T tokens之后，7B参数模型的性能仍在继续提高。

[!NOTE]

虽然大模型可能需要更少的数据就能达到特定性能（训练阶段看似高效）。但从长期来看，小模型虽然需要更多训练数据和时间，但因其推理成本低，在大规模部署时更具经济优势

本工作的重点是通过训练时使用比通常更多的tokens，来训练一系列在各种推理预算下能够获得最佳性能的语言模型。由此产生的模型，称为LLaMA，其参数规模从7B到65B不等，与现有最佳的LLMs相比具有竞争力的性能。例如，LLaMA-13B在大多数基准测试上超过了GPT-3，尽管它小10倍。我们相信这个模型将有助于使LLMs的访问和研究更加民主化，因为它可以在单个GPU上运行。在更高端的规模上，我们的65B参数模型也与最佳的大型语言模型（如Chinchilla或PaLM-540B）具有竞争力。

与Chinchilla、PaLM或GPT-3不同，我们只使用公开可获取的数据，使我们的工作与开源兼容，而大多数现有模型依赖于非公开或未记录的数据（例如"Books–2TB"或"社交媒体对话"）。也有一些例外，特别是OPT（Zhang等，2022）、GPT-NeoX（Black等，2022）、BLOOM（Scao等，2022）和GLM（Zeng等，2022），但没有一个能与PaLM-62B或Chinchilla竞争。

在本文的其余部分，我们将概述我们对transformer架构（Vaswani等，2017）所做的修改，以及我们的训练方法。然后，我们报告我们的模型的性能，并在一系列标准基准测试上与其他LLMs进行比较。最后，我们使用负责任AI社区的一些最新基准测试，揭示了我们模型中编码的一些偏见和有害内容。

[!NOTE]

LLaMA的核心创新在于：1)利用大量tokens训练较小模型，在各种推理预算下实现最佳性能；2)规模从7B到65B参数，性能出色(13B版本超越参数量大10倍的GPT-3)；3)完全使用公开数据训练，支持开源研究；4)小型版本可在单GPU上运行，使AI研究更加民主化。

2 方法

我们的训练方法与之前工作中所描述的方法相似（Brown等，2020；Chowdhery等，2022），并受到Chinchilla缩放法则的启发（Hoffmann等，2022）。我们使用标准优化器在大量文本数据上训练大型transformers模型。

2.1 预训练数据

我们的训练数据集是由表1中报告的几种来源混合组成的，涵盖了多个领域。在很大程度上，我们重用了已被其他LLMs利用的数据来源，但限制仅使用公开可获取的数据，并且与开源兼容。这导致以下数据混合及其在训练集中所占的百分比：

英文CommonCrawl [67%]。我们使用CCNet管道（Wenzek等，2020）预处理了2017年至2020年的五个CommonCrawl数据转储。这个过程在行级别进行去重，使用fastText线性分类器进行语言识别以删除非英语页面，并使用n-gram语言模型过滤低质量内容。此外，我们训练了一个线性模型来分类被用作维基百科参考的页面与随机抽样页面，并丢弃了未被分类为参考的页面。

C4 [15%]。在探索性实验中，我们观察到使用多样化的预处理CommonCrawl数据集可以提高性能。因此，我们在数据中包含了公开可用的C4数据集（Raffel等，2020）。C4的预处理也包含去重和语言识别步骤：与CCNet的主要区别在于质量过滤，C4主要依赖于启发式方法，如标点符号的存在或网页中的单词和句子数量。

GitHub [4.5%]。我们使用Google BigQuery上可用的公共GitHub数据集。我们只保留了根据Apache、BSD和MIT许可证分发的项目。此外，我们基于行长度或字母数字字符比例的启发式方法过滤了低质量文件，并使用正则表达式删除了样板文本（如页眉）。最后，我们在文件级别上通过精确匹配对结果数据集进行去重。

维基百科 [4.5%]。我们添加了2022年6月至8月期间的维基百科转储，涵盖20种使用拉丁或西里尔字母的语言：保加利亚语(bg)、加泰罗尼亚语(ca)、捷克语(cs)、丹麦语(da)、德语(de)、英语(en)、西班牙语(es)、法语(fr)、克罗地亚语(hr)、匈牙利语(hu)、意大利语(it)、荷兰语(nl)、波兰语(pl)、葡萄牙语(pt)、罗马尼亚语(ro)、俄语(ru)、斯洛文尼亚语(sl)、塞尔维亚语(sr)、瑞典语(sv)和乌克兰语(uk)。我们处理数据以移除超链接、评论和其他格式化样板文本。

古腾堡计划和Books3 [4.5%]。我们在训练数据集中包含了两个书籍语料库：古腾堡计划，其中包含公共领域的书籍，以及ThePile（Gao等，2020）中的Books3部分，这是一个用于训练大型语言模型的公开可用数据集。我们在书籍级别进行去重，删除内容重叠超过90%的书籍。

ArXiv [2.5%]。我们处理arXiv的Latex文件，向数据集添加科学数据。遵循Lewkowycz等人(2022)的方法，我们删除了第一部分之前的所有内容以及参考文献。我们还从.tex文件中移除了注释，并内联展开了用户编写的定义和宏，以增加论文之间的一致性。

Stack Exchange [2%]。我们包含了Stack Exchange的数据转储，这是一个包含高质量问题和答案的网站，涵盖了从计算机科学到化学的多个领域。我们保留了28个最大网站的数据，从文本中删除了HTML标签，并按得分对答案进行排序（从高到低）。

分词器。我们使用字节对编码(BPE)算法（Sennrich等，2015）对数据进行分词，使用了SentencePiece（Kudo和Richardson，2018）的实现。值得注意的是，我们将所有数字拆分为单个数字，并回退到字节以分解未知的UTF-8字符。

总体而言，我们的整个训练数据集在分词后包含大约1.4T个tokens。对于我们的大部分训练数据，每个token在训练过程中只使用一次，但维基百科和图书领域的数据例外，我们对这些数据大约进行了两个训练周期（epochs）。

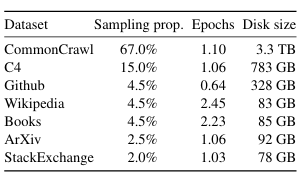
在这里插入图片描述

表1：预训练数据。 用于预训练的数据混合，对于每个子集，我们列出了采样比例、在1.4T tokens上训练时对该子集执行的训练周期数（epochs）以及磁盘大小。在1T tokens上的预训练运行具有相同的采样比例。

[!NOTE]

LLaMA采用类似之前大型语言模型的训练方法，但严格只使用公开可获取数据。训练数据（约1.4万亿tokens）由多种来源组成：英文CommonCrawl(67%)、C4(15%)、GitHub开源代码(4.5%)、20种语言的维基百科(4.5%)、书籍语料库(4.5%)、ArXiv科学论文(2.5%)和Stack Exchange问答(2%)。各数据源均经过严格预处理，包括去重、语言识别和质量过滤。模型使用字节对编码(BPE)算法进行分词，大部分数据仅在训练中使用一次，而维基百科和书籍数据使用了约两个训练周期。这种多样化且经过精心处理的数据集是LLaMA性能表现优异的关键因素之一。

[!IMPORTANT]

字节对编码(Byte Pair Encoding, BPE)是现代大语言模型中广泛应用的分词算法，它通过迭代合并最频繁出现的相邻字符对或子词对来构建词汇表，从而在保持较小词汇量的同时有效表示丰富文本。BPE的核心思想是从字符级表示开始，统计文本中相邻单元的共现频率，然后贪婪地合并最常见模式，这一过程不断重复直至达到预定词汇量，使模型能够自动学习语言的内部结构，如词根、词缀和常用词。

字节对编码(BPE)算法的完整流程如下：

准备阶段

数据收集：准备大量训练文本语料库

初始化：将所有单词拆分为最基本单位（通常是单个字符或字节）

构建基础词汇表：收集所有基本单位形成初始词汇表

准备阶段返回一个初始词汇表: 包含所有原子级别符号(通常是字符或字节)

训练阶段

统计频率：计算整个语料库中所有相邻符号对的出现频次

选择合并对：找出频率最高的相邻符号对

执行合并：将该符号对合并为一个新符号，添加到词汇表

更新语料库：在整个语料库中替换该符号对的所有出现

重复过程：返回步骤1，继续统计和合并

终止条件：达到预设词汇表大小或合并操作次数时停止

训练阶段结束返回完整词汇表，包含所有基本符号及合并产生的子词；合并规则列表，按优先级顺序排列的所有合并操作。

应用阶段

加载词汇表和合并规则：使用训练好的模型

新文本处理：将输入文本初始化为字符序列

按顺序应用合并规则：遵循训练时确定的合并顺序

输出分词结果：生成适合模型输入的子词序列

2.2 架构

遵循关于大型语言模型的最新工作，我们的网络基于transformer架构（Vaswani等，2017）。我们利用了随后提出的各种改进，这些改进被用于不同的模型，如PaLM。以下是与原始架构的主要区别，以及我们发现这些改变灵感的来源（在括号中）：

import math
from dataclasses import dataclass
from typing import Optional, Tuple

import fairscale.nn.model_parallel.initialize as fs_init
import torch
import torch.nn.functional as F
from fairscale.nn.model_parallel.layers import (
    ColumnParallelLinear,
    ParallelEmbedding,
    RowParallelLinear,
)
from torch import nn

# 相关参数
@dataclass
class ModelArgs:
    # 隐藏层的维度
    dim: int = 4096
    # Transformer 的层数
    n_layers: int = 32
    # 多头注意力机制的头数
    n_heads: int = 32
    # 键（Key）和值（Value）的头数
    n_kv_heads: Optional[int] = None
    # 模型的词汇表大小 稍后会根据分词器进行调整
    vocab_size: int = -1
    # 用于确保模型中某些特定维度是某个数值的倍数的参数 用于优化计算速度
    multiple_of: int = 256
    # 前馈层维度的倍率因子
    ffn_dim_multiplier: Optional[float] = None
    # 前馈层的稳定性因子 用在RMSNorm中
    norm_eps: float = 1e-5
    # 最大批次大小
    max_batch_size: int = 32
    # 最大序列长度
    max_seq_len: int = 2048

预归一化 [GPT3]。为了提高训练稳定性，我们对每个transformer子层的输入进行归一化，而不是对输出进行归一化。我们使用由Zhang和Sennrich（2019）引入的RMSNorm归一化函数。

[!IMPORTANT]

RMSNorm是一种计算高效的归一化技术，它通过简化传统的层归一化方法，专注于调节输入向量的整体幅度，同时保留其方向信息。

RMSNorm的核心操作可以表示为： $RMSNorm(x)=aiRMS(a)⋅gi\text{RMSNorm}(x) = \frac{a_i}{\text{RMS}(a)} \cdot g_i$

其中，RMS函数计算如下： $RMS(a)=1n∑i=1nai2\text{RMS}(a) = \sqrt{\frac{1}{n}\sum_{i=1}^{n}a_i^2}$ 完整表达式为： $RMSNorm(a)=a1n∑i=1nai2⋅g\text{RMSNorm}(a) = \frac{a}{\sqrt{\frac{1}{n}\sum_{i=1}^{n}a_i^2}} \cdot g$

$a$ 表示输入激活向量
$n$ 是向量维度
$g$ 是可学习的缩放参数向量

RMSNorm通过移除均值中心化步骤简化了LayerNorm：

LayerNorm: $LN(a)=a−μσ2+ϵ⋅g+b\text{LN}(a) = \frac{a - \mu}{\sqrt{\sigma^2 + \epsilon}} \cdot g + b$
其中 $μ\mu$ 是均值， $σ2\sigma^2$ 是方差， $b$ 是偏置参数

RMSNorm: $RN(a)=a1n∑i=1nai2+ϵ⋅g\text{RN}(a) = \frac{a}{\sqrt{\frac{1}{n}\sum_{i=1}^{n}a_i^2 + \epsilon}} \cdot g$
直接使用RMS统计量进行归一化

这种简化降低了约40%的计算成本，同时在实验证明中保持了与LayerNorm相当的性能。

计算效率更高（无需计算均值）
参数量减少（没有偏置参数）
对深层神经网络训练提供稳定的梯度流

归一化策略公式统计维度参数优势劣势应用场景
批归一化 $\frac{x - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} \cdot \gamma + \beta$ 批次维度 $γ\gamma$ , $β\beta$ 加速收敛，允许更高学习率，适合CNN 小批量训练不稳定；分布式训练需同步批统计量 CNN、密集网络
层归一化 $\frac{x - \mu_L}{\sqrt{\sigma_L^2 + \epsilon}} \cdot \gamma + \beta$ 特征维度 $γ\gamma$ , $β\beta$ 批量大小无关，适合RNN/NLP任务，训练与推理一致特征间归一化可能破坏信息；CNN中效果不如批归一化 RNN、Transformer
RMS归一化 $\frac{x}{\sqrt{\frac{1}{n}\sum_{i=1}^{n}x_i^2} + \epsilon} \cdot \gamma$ 特征维度（无均值中心化） $γ\gamma$ 计算效率高，参数量少，适合深层网络移除均值中心化可能损失信息 LLaMA等大型语言模型

归一化策略	公式	统计维度	参数	优势	劣势	应用场景
批归一化	$\frac{x - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} \cdot \gamma + \beta$	批次维度	$γ\gamma$ , $β\beta$	加速收敛，允许更高学习率，适合CNN	小批量训练不稳定；分布式训练需同步批统计量	CNN、密集网络
层归一化	$\frac{x - \mu_L}{\sqrt{\sigma_L^2 + \epsilon}} \cdot \gamma + \beta$	特征维度	$γ\gamma$ , $β\beta$	批量大小无关，适合RNN/NLP任务，训练与推理一致	特征间归一化可能破坏信息；CNN中效果不如批归一化	RNN、Transformer
RMS归一化	$\frac{x}{\sqrt{\frac{1}{n}\sum_{i=1}^{n}x_i^2} + \epsilon} \cdot \gamma$	特征维度（无均值中心化）	$γ\gamma$	计算效率高，参数量少，适合深层网络	移除均值中心化可能损失信息	LLaMA等大型语言模型

class RMSNorm(torch.nn.Module):
    # 初始化方法
    def __init__(self, dim: int, eps: float = 1e-6):
        """
        参数:
            dim (int): 输入张量的最后一维的大小（特征维度）。
            eps (float, 可选): 一个很小的值，加到分母上以确保数值稳定性。默认是 1e-6。
        属性:
            eps (float): 一个很小的值，用于保证数值稳定性。
            weight (nn.Parameter): 可学习的缩放参数，用于调整归一化后的输出。
        """
        super().__init__()
        self.eps = eps
        # 将缩放参数初始化为全1
        self.weight = nn.Parameter(torch.ones(dim))

    #   对输入张量应用 RMSNorm 归一化。
    def _norm(self, x):
        """
        参数:
            x (torch.Tensor): 输入张量。 形状(batch_size, seq_len, dim)
            - batch_size：批量大小
            - seq_len：序列长度
            - dim：特征维度
        返回:
            torch.Tensor: 归一化后的张量。(batch_size, seq_len, dim)
        """
        # 计算均方根值 (RMS)，并将 x 按均方根值归一化
        # torch.rsqrt() 用于计算平方根倒数
        # mean(-1, keepdim=True)
        return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)

    # 通过RMSNorm层的前向传播。
    def forward(self, x):
        # 将输入张量转换为浮点数32，归一化后再转换回原数据类型
        output = self._norm(x.float()).type_as(x)
        # 使用可学习的缩放参数对张量进行缩放
        return output * self.weight
# x (batch_size, seq_len, dim)
# x.pow(2) (batch_size, seq_len, dim)
# mean(-1, keepdim=True)  -> (batch_size, seq_len, 1)
# +self.eps   -> (batch_size, seq_len, 1) (加一个数 自动广播)
# torch.rsqrt(...)  -> (batch_size, seq_len, 1) (取倒数平方根,不改变张量的形状)
# x * ... (广播机制)-> (batch_size, seq_len, dim) (均方根结果会自动广播成(batch_size, seq_len, dim)
# *是逐元素乘 [1,2]*[3,4]=[3,8]

[!CAUTION]

关于x.mean(dim=-1, keepdim=True)

# 假设输入的张量是
x = torch.tensor([
 [[1.0, 2.0, 3.0], 
  [4.0, 5.0, 6.0]],

 [[7.0, 8.0, 9.0], 
  [10.0, 11.0, 12.0]]
])
# x 的形状为 (2, 2, 3)
output = x.mean(dim=-1, keepdim=True)
# tensor([[[2.0],
#          [5.0]],
# 
#         [[8.0],
#          [11.0]]]) 输出形状为 (2, 2, 1)
# 如果 keepdim=False：
output = x.mean(dim=-1, keepdim=False)
# tensor([[ 2.0,  5.0],
#         [ 8.0, 11.0]]) 缺少一个维度会导致后续计算不匹配

SwiGLU激活函数 (SwiGLU activation function) [PaLM]。我们用Shazeer（2020）引入的SwiGLU激活函数替换了ReLU (Rectified Linear Unit) 非线性函数，以提高性能。我们使用 $23×4d\frac{2}{3} \times 4d$ 的维度，而不是PaLM中的 $4 d$ 。

[!NOTE]

ReLU通过简单的非线性变换，为神经网络引入非线性能力，从而提高模型的表达能力。表达式为:

$\max(0, x)$

当 $x > 0$ 时， $f (x) = x$ ；
当 $\leq 0$ 时， $f (x) = 0$ 。

[!IMPORTANT]

SwiGLU的公式如下：
$\text{SwiGLU}(X) = (XW_1) \odot \text{SiLU}(XW_2)$

其中：

$X$ 是输入矩阵或向量；
$W_1$ 和 $W_2$ 是权重矩阵；
$⊙\odot$ 表示逐元素乘法（Hadamard乘积）；
$SiLU(x)=x⋅σ(x)\text{SiLU}(x) = x \cdot \sigma(x)$ 是一种激活函数，也称为Swish，其中 $σ(x)\sigma(x)$ 是Sigmoid函数。

旋转位置编码 [GPTNeo]。我们移除了绝对位置编码，取而代之的是在网络的每一层添加由Su等人（2021）引入的旋转位置编码（RoPE）。

[!NOTE]

由于Transformer模型是并行处理的词语的，模型不知道单词的顺序，所以要给嵌入添加位置编码。《Attention is all you need》中使用固定的正弦和余弦函数生成位置向量并将位置编码直接加到词嵌入上；提供绝对位置信息，相对位置关系必须通过计算绝对位置的差值间接获得，自注意力本身对序列顺序是不敏感的。旋转位置编码（RoPE）通过复平面上的旋转操作编码位置；直接在注意力计算中体*相对位置关系，两个位置间的相对距离在它们的点积中自然表达。

# 负责生成用于后续旋转操作的复数频率表示u
# "频率"指的是旋转角度随位置变化的速率。
# 高频旋转：位置每向后移动一步，向量旋转角度很大（比如每步旋转60度）
# 低频旋转：位置每向后移动一步，向量旋转角度很小（比如每步旋转5度）
# 使用不同的维度，模型同时获得短距离和长距离的位置信息。高频维度提供精确信息，低频维度提供模糊但有用的信息。
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
    """
    参数:
        dim (int): 频率张量的维度。
        end (int): 用于预计算频率的结束索引。
        theta (float, 可选): 用于频率计算的缩放因子，默认为 10000.0。
    返回:
        torch.Tensor: 预计算的复数指数频率张量。
    """
    # torch.arange(0, dim, 2) → 生成 [0, 2, 4, ..., dim-2] 的序列
    # [: (dim // 2)] 取前(dim//2个)确保形状是[dim//2]
    # .float() / dim 进行归一化到接近[0,1)
    # theta ** (...) 计算10000^(i/dim) 原始transformer使用(pos/10000^(2i/d_model))作为
    # 1.0 / (...) 取倒数，得到最终频率 先计算出 (1.0 / 10000^(2i/dim))
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
    # 确保其与freqs在同一位置 t的形状是[end]
    t = torch.arange(end, device=freqs.device)  # type: ignore
    # 计算外积 torch.outer(t, freqs) 创建矩阵，其中 M[i,j] = t[i] * freqs[j] 得到每个位置与每个频率的乘积
    freqs = torch.outer(t, freqs).float()  # type: ignore 形状：[end, dim//2]
    # torch.polar(magnitude, angle) 使用复平面进行计算
	# -magnitude: 复数的模长（这里全是1）
	# -angle: 复数的辐角（在这里是freqs）
	# 其中的元素的值为 e^(i*freqs[pos, d])
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs)  # complex64
    return freqs_cis	# 形状[end, dim//2]

[!WARNING]

欧拉公式:
$e^{i\theta} = \cos(\theta) + i\sin(\theta)$
在复平面中，一个复数可以表示为：$ z = r e^{i\theta} = r (\cos\theta + i\sin\theta) $

其中：

r 是复数的模长（向量长度）
θ 是复数的辐角（向量与正实轴的夹角）

当 $r = 1$ 时，复数 $eiθe^{i\theta}$ 表示单位圆上的一个点，即一个旋转角度为 $θ\theta$ 的单位向量。

复指数形式 $ei⋅freqs[pos,d]e^{i \cdot \text{freqs}[pos, d]}$ 可以通过欧拉公式进行展开：
$e^{i \cdot \text{freqs}[pos, d]} = \cos(\text{freqs}[pos, d]) + i \sin(\text{freqs}[pos, d])$

[!WARNING]

RoPE 的频率设计灵感来源于 Transformer 的位置编码公式。对于维度 $d$ ，其频率 $Θd\Theta_d$ 定义为：
$\Theta_d = \frac{1}{10000^{2d/D}}$

其中：

$d$ 是当前维度索引 $\leq d < D/2)$
$D$ 是向量的总维度

解释：

低维度（ $d$ 小）具有高频率 $Θd\Theta_d$ ，适合捕捉局部（近距离）关系
高维度（ $d$ 大）具有低频率 $Θd\Theta_d$ ，适合捕捉全局（远距离）关系

# 将频率张量调整为与目标张量 'x' 相同的形状，以便在执行逐元素操作时进行广播。
def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
    """
    参数:
        freqs_cis (torch.Tensor): 需要调整形状的频率张量。
        x (torch.Tensor): 用于广播的目标张量。
    返回:
        torch.Tensor: 调整后的频率张量。
    """
    # 首先要确保x的维度大于2 后续处理依赖于第一维和最后一维
    ndim = x.ndim
    assert 0 <= 1 < ndim
    # 保证freqs_cis
    assert freqs_cis.shape == (x.shape[1], x.shape[-1])
    # 构建一个新矩阵 
    # 遍历 x 的每一维，检查当前维度的索引：
    # 如果索引是 1 或 ndim - 1（即第 1 维或最后一维），保留原来的大小 d。否则，将该维设置为 1。
    shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
    # 调整形状
    return freqs_cis.view(*shape)

# 输入向量的形状是:(batch_size, seq_len, hidden_dim),但是频率张量的形状是(seq_len, hidden_dim)。所以要进行上述操作。
# 例如：freqs_cis.shape = (64, 128)	x.shape = (8, 64, 128) 	freqs_cis->(1,64,128)

# 使用给定的频率张量对查询和键应用旋转嵌入。
def apply_rotary_emb(
    xq: torch.Tensor,
    xk: torch.Tensor,
    freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
    """
    参数:
        xq (torch.Tensor): 用于应用旋转嵌入的查询张量。
        xk (torch.Tensor): 用于应用旋转嵌入的键张量。
        freqs_cis (torch.Tensor): 为复数指数预先计算的频率张量。

    返回:
        Tuple[torch.Tensor, torch.Tensor]: 包含旋转嵌入的修改后查询张量和键张量的元组。
    """
    # 首先要将xq化成float类型 方便复数计算
    # xq.shape = (batch_size, seq_len, hidden_dim)
    # xq.shape[:-1] 获取除了最后一维之外的所有维度 (batch_size, seq_len)
    # *用于解包操作 *(batch_size,seq_len) = batch_size, seq_len
    # -1用于占位 会自动计算 2 表示最后一维的大小定为2
    # xq.float().reshape(*xq.shape[:-1], -1, 2) 的维度是 (batch_size, seq_len, hidden_dim//2, 2)
    # 将张量的最后一维拆分成两部分 用于表示复数的实部和虚部
    # [1.0, 2.0, 3.0, 4.0]  ->       [[1.0, 2.0],  # 第一个复数 (1.0 + 2.0j)
    #                                [3.0, 4.0]]  # 第二个复数 (3.0 + 4.0j)
    # torch.view_as_complex(...)：将最后一维的两部分（实部和虚部）组合成复数张量。
    # 最后xq_的形状是 (batch_size, seq_len, hidden_dim // 2)
    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
    # 使用上文函数使频率函数符合广播条件 ->(1, seq_len, hidden_dim // 2)
    freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
    # xq_ * freqs_cis 将复数张量 xq_ 与频率张量 freqs_cis 相乘，实现旋转嵌入
    # torch.view_as_real 将结果从复数形式转换回实数形式，拆分为实部和虚部
    # (batch_size, seq_len, hidden_dim // 2) -> (batch_size, seq_len, hidden_dim // 2, 2)
    # .flatten(3)：将最后两维（hidden_dim // 2 和 2）展开为一维 -> (batch_size, seq_len, hidden_dim)
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
    return xq_out.type_as(xq), xk_out.type_as(xk)

# 对输入向量的x维度进行拓展
def repeat_kv(x: torch.Tensor, n_rep: int) -> torch.Tensor:
    """
    参数:
        x (torch.Tensor): 输入的键值张量，形状为 (batch_size, seq_len, n_kv_heads, head_dim)。
        n_rep (int): 重复的次数。

    返回:
        torch.Tensor: 重复后的张量，形状为 (batch_size, seq_len, n_kv_heads * n_rep, head_dim)。
    """
    # bs：批量大小（batch size）
    # slen：序列长度（sequence length）
    # n_kv_heads：键值头的数量
    # head_dim：每个头的特征维度
    bs, slen, n_kv_heads, head_dim = x.shape
    # 只重复一次 则可直接返回原向量
    if n_rep == 1:
        return x
    return (
        # x[:, :, :, None, :] 增加了一个新的维度 -> (batch_size, seq_len, n_kv_heads, 1, head_dim)
        x[:, :, :, None, :]
        # 沿着新维度重复n_rep次 -> (batch_size, seq_len, n_kv_heads, n_rep, head_dim)
        .expand(bs, slen, n_kv_heads, n_rep, head_dim)
        # 重新调整形状
        .reshape(bs, slen, n_kv_heads * n_rep, head_dim)
    )

RoPE的核心思想是通过旋转变换将位置信息嵌入到输入向量中。具体来说：

输入向量

假设输入向量为 $\in \mathbb{R}^d$ ，其中 $d$ 是向量的维度。

旋转变换

为每个位置 $i$ 定义一个旋转矩阵 ( R(i) )，其作用是对输入向量 $q_i$ 和 $k_i$ 的前半部分和后半部分分别施加旋转操作。具体公式为：
$q_i^{\text{rot}} = R(i) \cdot q_i, \quad k_i^{\text{rot}} = R(i) \cdot k_i$

相对位置编码

通过旋转变换，位置 $i$ 和位置 $j$ 的相对关系可以通过旋转编码的内积表示为：
$q_i^{\text{rot}} \cdot k_j^{\text{rot}} = (q_i \cdot R(i - j)) \cdot k_j$

其中，旋转矩阵 $R (i - j)$ 使得编码中显式包含了位置差 ( i - j )，从而实现了相对位置关系的建模。

我们不同模型的超参数详情在表2中给出。

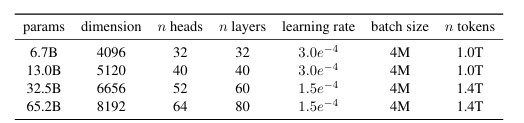
在这里插入图片描述

表2：模型大小、架构和优化超参数。

2.3 优化器

[!NOTE]

Adam（Adaptive Moment Estimation）它结合了 SGD（随机梯度下降）的动量方法和 RMSProp 的自适应学习率方法，能够在多数场景下快速收敛并提供较好的性能。

Adam 的更新规则通过一阶和二阶动量估计来调整每个参数的学习率。具体公式如下：

梯度计算

计算目标函数 $f(θ)f(\theta)$ 的梯度：
$g_t = \nabla_{\theta_t} f(\theta_t)$
其中 $t$ 是当前时间步， $θt\theta_t$ 是参数。

一阶动量（均值）的估计

使用指数加权移动平均计算梯度的均值：
$m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t$

$m_t$ ：梯度的一阶动量（均值）。
$β1\beta_1$ ：一阶动量的衰减系数（通常为 0.9）。

二阶动量（方差）的估计

使用指数加权移动平均计算梯度平方的均值：
$v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2$

$v_t$ ：梯度的二阶动量（未中心化的方差）。
$β2\beta_2$ ：二阶动量的衰减系数（通常为 0.999）。

偏差校正

为了修正初始时 $m_t$ 和 $v_t$ 的偏差（因为初始时 $m_0$ 和 $v_0$ 为零），进行以下校正：
$m^t=mt1−β1t,v^t=vt1−β2t \hat{m}_t = \frac{m_t}{1 - \beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1 - \beta_2^t}$

参数更新

使用校正后的动量估计更新参数：
$θt+1=θt−η⋅m^tv^t+ϵ \theta_{t+1} = \theta_t - \eta \cdot \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon}$

$η\eta$ ：学习率（通常为 1e-3）。
$ϵ\epsilon$ ：防止分母为零的小值（通常为 1e-8）。

特性

自适应学习率：

Adam 为每个参数动态调整学习率，能够适应不同的梯度变化。

结合动量：

使用动量方法平滑梯度更新，减少震荡。

收敛速度快：

Adam 通常比 SGD 和其他优化器收敛更快，适合处理稀疏梯度和高噪声梯度问题。

默认超参数效果良好：

$β1=0.9\beta_1 = 0.9$ 、 $β2=0.999\beta_2 = 0.999$ 、 $η=1e−3\eta = 1e-3$ 通常无需调参即可获得良好效果。

我们的模型使用AdamW优化器（Loshchilov和Hutter，2017）进行训练，具有以下超参数：β₁ = 0.9，β₂ = 0.95。

[!IMPORTANT]

AdamW 将权重衰减从梯度更新中解耦，改为显式地对参数进行衰减。其更新公式为：
$θt+1=θt−η⋅m^tv^t+ϵ−ηλθt \theta_{t+1} = \theta_t - \eta \cdot \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} - \eta \lambda \theta_t$

最后一项 $−ηλθt-\eta \lambda \theta_t$ 是显式的权重衰减，与梯度更新无关。
这种方式确保了权重衰减的效果仅作用于参数本身，而不会干扰梯度的更新。

我们使用余弦学习率调度，使最终学习率等于最大学习率的10%。我们使用0.1的权重衰减和1.0的梯度裁剪。我们使用2000个预热步骤，并根据模型的大小调整学习率和批量大小（详情见表2）。

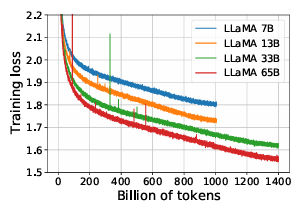
在这里插入图片描述

图1：7B、13B、33B和65B模型在训练token (train tokens) 上的训练损失 (training loss) 曲线LLaMA-33B和LLaMA-65B在1.4T token上进行了训练。较小的模型在1.0T token上进行了训练。所有模型都使用4M token的批量大小 (batch size) 进行训练。

[!NOTE]

余弦学习率调度公式：

$\eta_t = \eta_{\text{min}} + \frac{1}{2} (\eta_{\text{max}} - \eta_{\text{min}}) \left(1 + \cos\left(\frac{t}{T} \pi\right)\right)$

其中：

$ηt\eta_t$ ：第 $t$ 步的学习率。
$ηmax\eta_{\text{max}}$ 和 $ηmin\eta_{\text{min}}$ ：学习率的最大值和最小值。
$T$ ：总的训练步数。

通过余弦函数的平滑特性，避免了学习率的突变。在训练后期，逐步降低学习率，使模型更稳定地收敛。
# 补充对应优化器的实现方法

2.4 高效实现

我们进行了几项优化以提高模型的训练速度。首先，我们使用了因果多头注意力 (causal multi-head attention) 的高效实现，以减少内存使用和运行时间。这个实现可在xformers库²中获得，受Rabe和Staats（2021）的启发，并使用了Dao等人（2022）的反向传播 (backward) 方法。这是通过不存储注意力权重以及不计算由于语言建模任务的因果性质而被掩蔽的键/查询分数 (key/query scores) 来实现的。

# 因果多头注意力实现 args (ModelArgs): 上面定义的数据配置类
class Attention(nn.Module):
    def __init__(self, args: ModelArgs):
        # 1.参数初始化与配置
        super().__init__()
        # 键和值的头部数量 默认为 n_heads，但可以通过 args.n_kv_heads 单独配置 n_kv_heads = 32
        self.n_kv_heads = args.n_heads if args.n_kv_heads is None else args.n_kv_heads
        # 使用分布式计算 获取模型并行的分块数量 假设 model_parallel_size = 2
        model_parallel_size = fs_init.get_model_parallel_world_size()
        # 每个GPU上的查询头的数目 n_local_heads = 32 // 2 = 16
        self.n_local_heads = args.n_heads // model_parallel_size
        # 每个GPU上的键值头的数目 n_local_kv_heads = 32 // 2 = 16
        self.n_local_kv_heads = self.n_kv_heads // model_parallel_size

        # 在多头注意力机制中，每个查询向量都需要与对应的键向量计算注意力分数，然后应用于对应的值向量。
        # 查询头和键值头的数量必须匹配，才能正确计算注意力
        # 键和值的头需要重复的次数 n_rep = 16 // 16 = 1 (无需重复)
        self.n_rep = self.n_local_heads // self.n_local_kv_heads

        # 每个头的特征维度
        # 多头注意力将单一的注意力机制分割成多个"头" 每个头专注于不同的特征子空间
        # 所有头的结果最终合并，提供更丰富的表示
        self.head_dim = args.dim // args.n_heads

        # xq = x @ wq.weight ^ T
        # 查询的线性变换 ColumnParallelLinear：标准线形层
        self.wq = ColumnParallelLinear(
            args.dim, # 输入维度
            args.n_heads * self.head_dim, # 输出维度
            bias=False, # 是否添加偏置
            # 是否收集分布式输出
            # False 表示不收集分散在各个 GPU 上的输出到单个 GPU
            # 保持输出分散状态，便于后续并行计算
            gather_output=False,
            # 权重初始化方法
            init_method=lambda x: x,
        )

        # 键的线性变换
        # xk = x @ wk.weight ^ T
        self.wk = ColumnParallelLinear(
            args.dim,
            self.n_kv_heads * self.head_dim,
            bias=False,
            gather_output=False,
            init_method=lambda x: x,
        )
        # 值的线性变换
        # xv = x @ wv.weight^T
        self.wv = ColumnParallelLinear(
            args.dim,
            self.n_kv_heads * self.head_dim,
            bias=False,
            gather_output=False,
            init_method=lambda x: x,
        )
        # 输出的线性变换
        self.wo = RowParallelLinear(
            args.n_heads * self.head_dim,
            args.dim,
            bias=False,
            input_is_parallel=True,
            init_method=lambda x: x,
        )
        # 键的缓存
        self.cache_k = torch.zeros(
            (
                args.max_batch_size,
                args.max_seq_len,
                self.n_local_kv_heads,
                self.head_dim,
            )
        ).cuda()
        # 值的缓存
        self.cache_v = torch.zeros(
            (
                args.max_batch_size,
                args.max_seq_len,
                self.n_local_kv_heads,
                self.head_dim,
            )
        ).cuda()

    # 注意力的前向传播函数
    def forward(
        self,
        x: torch.Tensor,
        start_pos: int,
        freqs_cis: torch.Tensor,
        mask: Optional[torch.Tensor],
    ):
        """
        参数:
            x (torch.Tensor): 输入张量。
            start_pos (int): 缓存的起始位置。
            freqs_cis (torch.Tensor): 预计算的频率张量。
            mask (torch.Tensor, optional): 注意力掩码张量。

        返回:
            torch.Tensor: 应用注意力后的输出张量。
        """
        # 2.输入处理与线性映射
        # 从输入向量x中提取批次大小和序列长度 不需要提取嵌入维度
        bsz, seqlen, _ = x.shape # (4, 256, 4096)
        xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)  # 输出都是(4, 256, 4096)
        # 重塑为多头形式 (4, 256, 32, 128)
        xq = xq.view(bsz, seqlen, self.n_local_heads, self.head_dim)
        xk = xk.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
        xv = xv.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
        # 应用旋转位置编码 (4, 256, 32, 128)
        xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)
        # 确保缓存张量与当前输入在相同设备和数据类型上
        self.cache_k = self.cache_k.to(xq)
        self.cache_v = self.cache_v.to(xq)
        # 将当前序列的键值对存入缓存的指定位置
        # 当前批次的键值 xk,xv: (bsz, seqlen, n_local_kv_heads, head_dim)
        # 被更新的缓存片段 (bsz, start_pos:start_pos+seqlen, n_local_kv_heads, head_dim)
        # 相关切片技巧复习
        # 第一个维度 :bsz 在批次维度上选择索引从0到bsz-1的全部数据
        # 第二个维度 start_pos : start_pos + seqlen 在序列维度上选择从start_pos开始，长度为seqlen的切片
        # xk、xv: 仅包含当前新输入的序列片段的键值对
        self.cache_k[:bsz, start_pos : start_pos + seqlen] = xk
        self.cache_v[:bsz, start_pos : start_pos + seqlen] = xv
        # 进行历史信息检索
        # keys、values: 包含从序列开始到当前位置的所有键值对
        keys = self.cache_k[:bsz, : start_pos + seqlen]
        values = self.cache_v[:bsz, : start_pos + seqlen]
        # 适应不同查询键值比例的优化 如果 n_kv_heads < n_heads，则重复键/值头
        # (bs, cache_len + seqlen, n_local_heads, head_dim)
        keys = repeat_kv(keys, self.n_rep)
        # (bs, cache_len + seqlen, n_local_heads, head_dim)
        values = repeat_kv(values, self.n_rep)
        # 重排维度顺序，为批量矩阵乘法准备，把头的维度提前有利于并行计算 这种排列使得GPU可以同时处理多个注意力头的计算
        # xq (bs, seqlen, n_local_heads, head_dim) -> (bs, n_local_heads, seqlen, head_dim)
        xq = xq.transpose(1, 2)
        # (bs, cache_len + seqlen, n_local_heads, head_dim)-> (bs, n_local_heads, cache_len + seqlen, head_dim)
        keys = keys.transpose(1, 2)
        values = values.transpose(1, 2)
        # 输出形状 (bs, n_local_heads, seqlen, cache_len + seqlen)
        # 计算公式同原始Transformer相同
        # 使用的是矩阵乘法
        scores = torch.matmul(xq, keys.transpose(2, 3)) / math.sqrt(self.head_dim)
        # 将掩码张量加到注意力分数上 保证softmax后接近0 形状不变
        if mask is not None:
            scores = scores + mask # mask: (1, 1, seqlen, cache_len + seqlen)
        # 在最后一个维度进行归一化 形状不变
        scores = F.softmax(scores.float(), dim=-1).type_as(xq)
        # 计算加权上下文
        # 进行矩阵乘法
        output = torch.matmul(scores, values)  # (bs, n_local_heads, seqlen, head_dim)
        # scores: (bs, n_local_heads, seqlen, cache_len + seqlen)
        # values: (bs, n_local_heads, cache_len + seqlen, head_dim)

        # 重组多头输出
        output = output.transpose(1, 2).contiguous().view(bsz, seqlen, -1)
        # output.transpose(1, 2): (bs, seqlen, n_local_heads, head_dim)
        # 合并最后两个维度后: (bs, seqlen, n_local_heads * head_dim)

        # 输出投影
        return self.wo(output)
        # 输入: (bs, seqlen, 4096)
        # self.wo: 线性层 权重形状(4096, 4096)
        # 最终输出: (bs, seqlen, 4096)

为了进一步提高训练效率，我们减少了在反向传播过程中需要重新计算的激活值 (activations) 数量，采用了检查点 (checkpointing) 技术。更准确地说，我们保存了那些计算成本高昂的激活值，例如线性层 (linear layers) 的输出。这是通过手动实现transformer层的反向函数 (backward function)，而不是依赖PyTorch自动求导 (PyTorch autograd) 来实现的。为了充分利用这一优化，我们需要通过使用模型并行和序列并行 (model parallelism and sequence parallelism)，如Korthikanti等人（2022）所描述的那样，来减少模型的内存使用。此外，我们还尽可能地重叠激活值的计算和GPU之间通过网络的通信（由all_reduce操作 (all_reduce operations) 引起）。

[!NOTE]

# 补充检查点相关内容

当训练一个65B参数的模型时，我们的代码在2048个配备80GB RAM的A100 GPU上处理速度约为每秒每GPU 380个tokens。这意味着在我们包含1.4T tokens的数据集上训练大约需要21天。

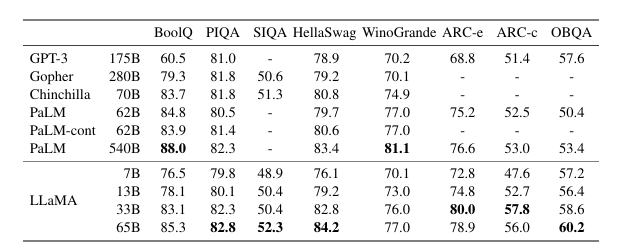
在这里插入图片描述

表3：常识推理任务 (Common Sense Reasoning tasks) 的零样本性能 (Zero-shot performance)。

3 主要结果

遵循先前工作（Brown等人，2020），我们考虑零样本 (zero-shot) 和少样本 (few-shot) 任务，并在总计20个基准测试上报告结果：

• 零样本。我们提供任务的文本描述和一个测试示例。模型要么通过开放式生成提供答案，要么对提议的答案进行排序。

• 少样本。我们提供任务的几个示例（1到64个之间）和一个测试示例。模型将此文本作为输入并生成答案或对不同选项进行排序。

我们将LLaMA与其他基础模型进行比较，即非公开可用的语言模型GPT-3（Brown等人，2020）、Gopher（Rae等人，2021）、Chinchilla（Hoffmann等人，2022）和PaLM（Chowdhery等人，2022），以及开源的OPT模型（Zhang等人，2022）、GPT-J（Wang和Komatsuzaki，2021）和GPT-Neo（Black等人，2022）。在第4节中，我们还简要比较了LLaMA与指令调优 (instruction-tuned) 模型，如OPT-IML（Iyer等人，2022）和Flan-PaLM（Chung等人，2022）。

我们评估LLaMA在自由格式生成任务和多项选择任务上的表现。在多项选择任务中，目标是在一组给定选项中选择最合适的完成项，基于提供的上下文。我们选择给定上下文条件下似然性最高的完成项。我们遵循Gao等人（2021）的方法，使用按完成项字符数归一化的似然性，除了某些数据集（OpenBookQA、BoolQ），对于这些数据集，我们遵循Brown等人（2020）的方法，基于完成项的似然性除以给定"Answer:"作为上下文的完成项似然性来选择完成项： $P(completion∣context)P(completion∣Answer:)\frac{P(\text{completion}|\text{context})}{P(\text{completion}|\text{Answer:})}$

3.1 常识推理 (Common Sense Reasoning)

我们考察了八个标准常识推理基准测试：BoolQ（Clark等人，2019）、PIQA（Bisk等人，2020）、SIQA（Sap等人，2019）、HellaSwag（Zellers等人，2019）、WinoGrande（Sakaguchi等人，2021）、ARC easy和challenge（Clark等人，2018）以及OpenBookQA（Mihaylov等人，2018）。这些数据集包括完形填空 (Cloze) 和Winograd风格任务，以及多项选择问答。我们在零样本 (zero-shot) 设置下进行评估，这是语言建模社区的常规做法。

在表3中，我们与各种规模的现有模型进行比较，并报告来自相应论文的数据。首先，LLaMA-65B在除BoolQ外的所有报告的基准测试上都优于Chinchilla-70B。类似地，这个模型在除BoolQ和WinoGrande之外的所有地方都超过了PaLM-540B。LLaMA-13B模型尽管比GPT-3小10倍，但在大多数基准测试上也优于GPT-3。

3.2 闭卷问答 (Closed-book Question Answering)

我们在两个闭卷问答基准测试上将LLaMA与现有的大型语言模型进行比较：Natural Questions（Kwiatkowski等人，2019）和TriviaQA（Joshi等人，2017）。对于这两个基准测试，我们在闭卷设置下报告精确匹配 (exact match) 性能，即模型无法访问包含回答问题证据的文档。在表4中，我们报告了Natural Questions的性能，在表5中，我们报告了TriviaQA的性能。在这两个基准测试上，LLaMA-65B在零样本和少样本设置中都达到了最先进的性能。更重要的是，尽管LLaMA-13B比GPT-3和Chinchilla小5-10倍，但在这些基准测试上也具有竞争力。这个模型在推理 (inference) 过程中可以在单个V100 GPU上运行。

在这里插入图片描述

表4：自然问答 (Natural Questions) 的精确匹配性能 (Exact match performance)。

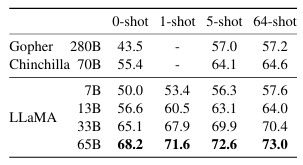
在这里插入图片描述

表5：TriviaQA。在过滤后的开发集 (filtered dev set) 上的零样本 (Zero-shot) 和少样本 (few-shot) 精确匹配性能 (exact match performance)。

3.3 阅读理解 (Reading Comprehension)

我们在RACE阅读理解基准测试（Lai等人，2017）上评估我们的模型。这个数据集收集自为中国中学和高中学生设计的英语阅读理解考试。我们遵循Brown等人（2020）的评估设置，并在表6中报告结果。在这些基准测试上，LLaMA-65B与PaLM-540B具有竞争力，而LLaMA-13B则比GPT-3高出几个百分点。

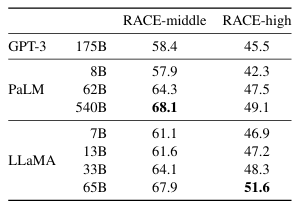
在这里插入图片描述

表6：阅读理解 (Reading Comprehension)。零样本准确率 (Zero-shot accuracy)。

3.4 数学推理 (Mathematical reasoning)

我们在两个数学推理基准测试上评估我们的模型：MATH（Hendrycks等人，2021）和GSM8k（Cobbe等人，2021）。MATH是一个包含12K个中学和高中数学问题的数据集，这些问题用LaTeX编写。GSM8k是一组中学数学问题集。在表7中，我们与PaLM和Minerva（Lewkowycz等人，2022）进行比较。Minerva是一系列在从ArXiv和数学网页提取的38.5B个token上微调的PaLM模型，而PaLM和LLaMA都没有在数学数据上进行微调。PaLM和Minerva的数据取自Lewkowycz等人（2022），我们对有无maj@k的情况进行了比较。maj@k表示一种评估方式，我们为每个问题生成k个样本并执行多数投票（Wang等人，2022）。在GSM8k上，我们观察到LLaMA-65B优于Minerva-62B，尽管它没有在数学数据上进行过微调。

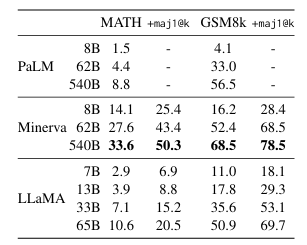
在这里插入图片描述

**表7：模型在定量推理数据集上的性能。**对于多数投票 (majority voting)，我们使用与Minerva相同的设置，MATH使用k=256个样本，GSM8k使用k=100（Minerva 540B对MATH使用k=64，对GSM8k使用k=40）。LLaMA-65B在GSM8k上的性能优于Minerva 62B，尽管它没有在数学数据上进行微调。

3.5 代码生成 (Code generation)

我们在两个基准测试上评估模型从自然语言描述生成代码的能力：HumanEval（Chen等人，2021）和MBPP（Austin等人，2021）。对于这两项任务，模型接收程序的几句话描述，以及几个输入-输出示例。在HumanEval中，它还接收函数签名，且提示被格式化为自然代码，包含文本描述和文档字符串 (docstring)。模型需要生成符合描述并满足测试用例的Python程序。在表8中，我们将我们模型的pass@1分数与现有的未在代码上微调的语言模型进行比较，即PaLM和LaMDA（Thoppilan等人，2022）。PaLM和LLaMA都在包含相似数量代码tokens的数据集上进行训练。

如表8所示，在相似参数量的情况下，LLaMA优于其他未专门为代码训练或微调的通用模型，如LaMDA和PaLM。拥有13B参数及以上的LLaMA在HumanEval和MBPP上都优于LaMDA-137B。LLaMA-65B也优于PaLM-62B，即使后者训练时间更长。本表中报告的pass@1结果是通过温度为0.1的采样获得的。pass@100和pass@80指标是通过温度为0.8的采样获得的。我们使用与Chen等人（2021）相同的方法来获得无偏的pass@k估计。

通过对代码特定tokens进行微调，可以提高代码性能。例如，PaLM-Coder（Chowdhery等人，2022）将PaLM在HumanEval上的pass@1分数从26.2%提高到36%。其他专门为代码训练的模型在这些任务上的表现也优于通用模型（Chen等人，2021；Nijkamp等人，2022；Fried等人，2022）。在代码tokens上进行微调超出了本文的范围。

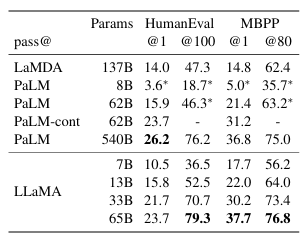
在这里插入图片描述

**表8：代码生成的模型性能。**我们报告了在HumanEval和MBPP上的pass@k分数。HumanEval生成是在零样本 (zero-shot) 设置下进行的，而MBPP使用类似于Austin等人（2021）的3-shot提示。标有*的值是从Chowdhery等人（2022）的图表中读取的。

3.6 大规模多任务语言理解 (Massive Multitask Language Understanding)

由Hendrycks等人（2020）引入的大规模多任务语言理解基准测试（MMLU）由涵盖各种知识领域的多项选择题组成，包括人文学科、STEM（科学、技术、工程和数学）和社会科学。我们在5-shot设置下评估我们的模型，使用基准测试提供的示例，并在表9中报告结果。在这个基准测试上，我们观察到LLaMA-65B平均落后于Chinchilla-70B和PaLM-540B几个百分点，且在大多数领域也是如此。一个可能的解释是我们在预训练数据中使用了有限数量的书籍和学术论文，即ArXiv、Gutenberg和Books3，总计仅177GB，而这些模型的训练数据包含多达2TB的书籍。Gopher、Chinchilla和PaLM使用的大量书籍可能也解释了为什么Gopher在这个基准测试上优于GPT-3，而在其他基准测试上它们的表现相当。

3.7 训练期间性能的演变 (Evolution of performance during training)

在训练期间，我们跟踪了模型在几个问答和常识基准测试上的性能，并在图2中报告了这些结果。在大多数基准测试上，性能稳步提高，并与模型的训练困惑度 (perplexity) 相关（见图1）。例外情况是SIQA和WinoGrande。尤其值得注意的是，在SIQA上，我们观察到性能有很大的方差，这可能表明该基准测试不可靠。在WinoGrande上，性能与训练困惑度的相关性不太高：LLaMA-33B和LLaMA-65B在训练期间表现相似。

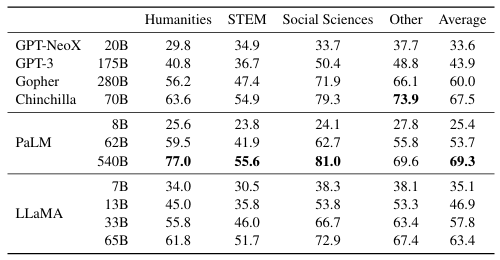
在这里插入图片描述

表9：大规模多任务语言理解 (MMLU)。五样本准确率 (Five-shot accuracy)。

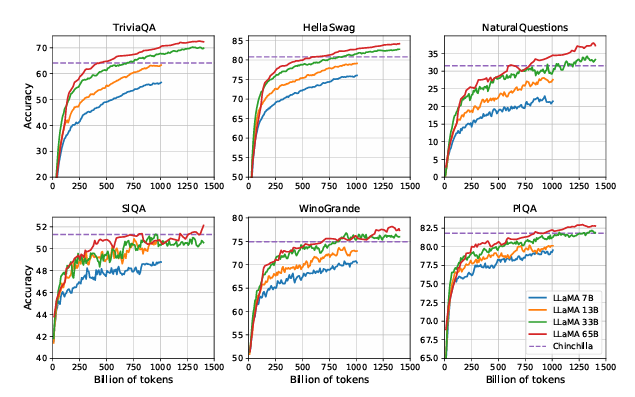
在这里插入图片描述

图2：在训练期间问答和常识推理性能的演变

4 指令微调 (Instruction Fine-tuning)

在本节中，我们展示在指令数据上进行简短的微调可以快速提升MMLU的性能。虽然未经微调的LLaMA-65B版本已经能够遵循基本指令，但我们观察到，少量的微调可以提高MMLU的性能，并进一步提升模型遵循指令的能力。由于这不是本文的重点，我们仅按照Chung等人(2022)的相同协议进行了一次实验，训练了一个指令模型，称为LLaMA-I。

在表10中，我们报告了我们的指令模型LLaMA-I在MMLU上的结果，并与现有的中等规模指令微调模型进行比较，即OPT-IML（Iyer等人，2022）和Flan-PaLM系列（Chung等人，2022）。所有报告的数字均来自相应的论文。尽管这里使用的指令微调方法很简单，我们在MMLU上达到了68.9%。LLaMA-I（65B）在MMLU上优于现有的中等规模指令微调模型，但与最先进的模型相比仍有差距，即GPT code-davinci-002在MMLU上达到77.4（数据来自Iyer等人（2022））。MMLU上57个任务的详细性能可以在附录的表16中找到。

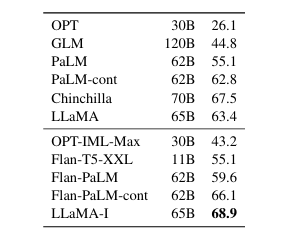
在这里插入图片描述

**表10：指令微调 - MMLU（5-shot）。**中等规模模型在MMLU上有无指令微调的比较。

5 偏见、毒性和错误信息 (Bias, Toxicity and Misinformation)

大型语言模型已被证明会复制并放大训练数据中存在的偏见（Sheng等人，2019；Kurita等人，2019），并生成有毒或冒犯性内容（Gehman等人，2020）。由于我们的训练数据集包含大量来自网络的数据，我们认为确定我们的模型生成此类内容的潜在可能性至关重要。为了了解LLaMA-65B的潜在危害，我们在不同的基准测试上进行评估，这些基准测试用于测量有毒内容的产生和刻板印象的检测。虽然我们选择了语言模型社区使用的一些标准基准测试来指出这些模型的一些问题，但这些评估还不足以充分理解与这些模型相关的风险。

5.1 真实毒性提示 (Real Toxicity Prompts)

语言模型可能生成有毒语言，例如侮辱、仇恨言论或威胁。模型可能生成的有毒内容范围非常广泛，这使得彻底评估变得具有挑战性。最近的一些研究（Zhang等人，2022；Hoffmann等人，2022）将RealToxicityPrompts基准测试（Gehman等人，2020）作为衡量模型毒性程度的指标。RealToxicityPrompts包含约10万个提示，模型必须完成这些提示；然后通过向PerspectiveAPI发出请求来自动评估毒性分数。我们无法控制第三方PerspectiveAPI使用的流程，这使得与之前的模型进行比较变得困难。

对于10万个提示中的每一个，我们使用模型以贪婪解码方式生成回应，并测量其毒性分数。每个提示的分数范围从0（非毒性）到1（毒性）。在表11中，我们报告了RealToxicityPrompts的基本提示和尊重提示类别的平均分数。这些分数与我们在文献中观察到的分数"相当"（例如，Chinchilla的分数为0.087），但这些工作与我们的方法学有所不同（在采样策略、提示数量和API时间方面）。我们观察到，随着模型规模的增加，毒性也会增加，尤其是对于尊重提示。这一现象在之前的研究中也有所观察（Zhang等人，2022），值得注意的例外是Hoffmann等人（2022）的研究，他们没有看到Chinchilla和Gopher之间有差异，尽管它们的规模不同。这可能是因为较大的模型Gopher的表现比Chinchilla差，这表明毒性与模型大小之间的关系可能只适用于同一模型系列内部。
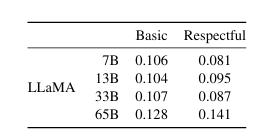
在这里插入图片描述

**表11：RealToxicityPrompts（真实毒性提示测试）。**我们在该基准测试的10万个提示上使用贪婪解码方式生成内容。其中"尊重型"提示是指以"请以礼貌、尊重和无偏见的方式完成以下句子："作为开头的提示，而"基本型"则不包含这一引导语。毒性评分是通过PerspectiveAPI获取的，分数越高表示生成的内容毒性越大。

5.2 CrowS-Pairs

我们在CrowS-Pairs数据集（Nangia等人，2020）上评估了模型中的偏见。该数据集允许测量9个类别的偏见：性别、宗教、种族/肤色、性取向、年龄、国籍、残疾、外表和社会经济地位。每个样本由一个刻板印象句子和一个反刻板印象句子组成，我们通过零样本设置下两个句子的困惑度来测量模型对刻板印象句子的偏好。因此，更高的分数表示更大的偏见。我们在表12中与GPT-3和OPT-175B进行了比较。

LLaMA总体上略优于这两个模型。我们的模型在宗教类别中表现出特别明显的偏见（比OPT-175B高10%），其次是年龄和性别类别。我们推测这些偏见可能来源于CommonCrawl数据，尽管我们已经进行了多步过滤。

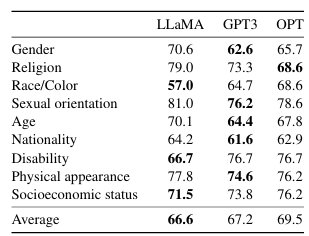
在这里插入图片描述

表12：CrowS-Pairs。我们比较了LLaMA-65B与OPT-175B和GPT3-175B模型中包含的偏见程度。分数越高表示偏见越大。

5.3 WinoGender

为了进一步研究我们模型在性别类别上的偏见，我们考察了WinoGender基准测试（Rudinger等人，2018），这是一个共指消解数据集。WinoGender由Winograd模式组成，评估偏见的方式是确定模型的共指消解性能是否受代词性别的影响。

更具体地说，每个句子有三个提及：一个"职业"，一个"参与者"，和一个"代词"，其中代词指代的是职业或参与者。我们提示模型确定共指关系，并根据句子的上下文衡量模型是否正确地进行了判断。目标是揭示模型是否捕捉到了与职业相关的社会偏见。例如，WinoGender数据集中的一个句子是"护士通知病人他的班次将在一小时内结束。“，接着是”'他’指的是"。然后我们比较"护士"和"病人"这两个续写的困惑度，以使用模型执行共指消解。我们评估了使用3种代词时的性能：“她/她的/她”，“他/他的/他"和"他们的/他们/某人”（不同选择对应代词的语法功能）。

在表13中，我们报告了数据集中三种不同代词的共指分数。我们观察到，我们的模型在处理"他们的/他们/某人"代词的共指消解时，表现明显优于处理"她/她的/她"和"他/他的/他"代词的情况。类似的观察也在之前的研究中被发现（Rae等人，2021；Hoffmann等人，2022），这可能表明存在性别偏见。事实上，在"她/她的/她"和"他/他的/他"代词的情况下，模型可能是使用职业的主流性别来执行共指消解，而不是使用句子中的证据。

为了进一步研究这一假设，我们查看了WinoGender数据集中"她/她的/她"和"他/他的/他"代词的一系列"陷阱"案例。这些案例对应于代词与职业的主流性别不匹配，且职业是正确答案的句子。在表13中，我们观察到我们的模型LLaMA-65B在陷阱示例上犯更多错误，清楚地表明它捕捉到了与性别和职业相关的社会偏见。"她/她的/她"和"他/他的/他"代词的性能下降都存在，这表明无论性别如何都存在偏见。

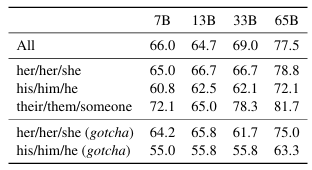
在这里插入图片描述

表13：WinoGender。LLaMA模型在不同代词（“她/她的/她"和"他/他的/他”）上的共指消解准确率。我们观察到我们的模型在"他们的/他们/某人"代词上获得了比"她/她的/她"和"他/他的/他"更好的性能，这很可能表明存在性别偏见。

5.4 TruthfulQA

TruthfulQA（Lin等人，2021）旨在测量模型的真实性，即其识别陈述是否真实的能力。Lin等人（2021）将"真实"定义为"关于现实世界的字面真相"，而非仅在某种信仰系统或传统背景下才成立的主张。这一基准测试可以评估模型生成错误信息或虚假主张的风险。测试问题以多样化的风格编写，涵盖38个类别，并且设计为对抗性的。

在表14中，我们报告了我们的模型在两个指标上的表现：真实性度量和真实且信息丰富的交集。与GPT-3相比，我们的模型在这两个类别中得分更高，但正确回答的比率仍然较低，表明我们的模型可能会产生不正确的幻觉回答。

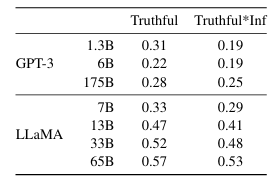
在这里插入图片描述

**表14：TruthfulQA。**我们报告了真实回答和真实且信息丰富回答的比例，这些评分由通过OpenAI API专门训练的模型给出。我们遵循Ouyang等人（2022）使用的问答提示风格，并报告了同一论文中GPT-3的性能。

6 碳足迹

我们模型的训练消耗了大量能源，导致二氧化碳排放。我们参考了该领域的最新文献，并在表15中详细分析了总能源消耗和由此产生的碳足迹。我们遵循Wu等人（2022）的公式来估算训练模型所需的瓦特小时（Wh）以及碳排放吨数（tCO2eq）。对于Wh，我们使用以下公式：

$Wh=GPU-h×(GPU功率消耗)×PUE\text{Wh} = \text{GPU-h} \times (\text{GPU功率消耗}) \times \text{PUE}$

其中PUE设为1.1。由此产生的碳排放取决于用于训练网络的数据中心的位置。例如，BLOOM使用的电网排放为0.057 kg CO2eq/KWh，导致27 tCO2eq；而OPT使用的电网排放为0.231 kg CO2eq/KWh，导致82 tCO2eq。在本研究中，我们有兴趣比较如果这些模型在同一数据中心训练，其训练过程的碳排放成本。因此，我们不考虑数据中心的位置，而是使用美国全国平均碳强度因子0.385 kg CO2eq/KWh。这导致以下碳排放吨数公式：

$tCO2eq=MWh×0.385\text{tCO2eq} = \text{MWh} \times 0.385$

为了公平比较，我们将相同的公式应用于OPT和BLOOM。对于OPT，我们假设训练需要在992个A100-80GB上进行34天（参见他们的日志）。最后，我们估计我们使用了2048个A100-80GB GPU，开发我们的模型大约持续了5个月。这意味着在我们的假设下，开发这些模型消耗了约2,638 MWh的能源，总排放量为1,015 tCO2eq。我们希望发布这些模型将有助于减少未来的碳排放，因为训练已经完成，并且一些模型相对较小，可以在单个GPU上运行。

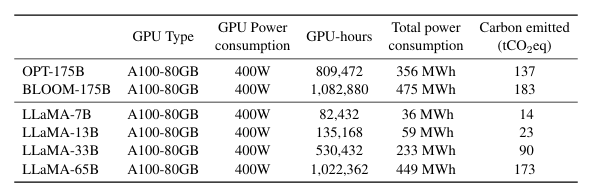
在这里插入图片描述

**表15：在相同数据中心训练不同模型的碳足迹。**我们遵循Wu等人（2022）的方法来计算在相同数据中心训练OPT、BLOOM和我们模型的碳排放量。对于A100-80GB的功率消耗，我们采用NVLink系统的热设计功率，即400W。我们采用1.1的PUE（电源使用效率）和美国全国平均碳强度因子0.385 kg CO2e/KWh。

7 相关工作

语言模型是词语、标记或字符序列上的概率分布（Shannon, 1948, 1951）。这一任务，通常被表述为下一个标记预测，长期以来被视为自然语言处理的核心问题（Bahl等人，1983；Brown等人，1990）。由于Turing（1950）提出通过"模仿游戏"使用语言来衡量机器智能，语言建模被提议作为衡量人工智能进展的基准（Mahoney, 1999）。

架构。 传统上，语言模型基于n-gram计数统计（Bahl等人，1983），并提出了各种平滑技术来改进对罕见事件的估计（Katz, 1987；Kneser和Ney, 1995）。在过去的二十年中，神经网络被成功应用于语言建模任务，从前馈模型开始（Bengio等人，2000），到循环神经网络（Elman, 1990；Mikolov等人，2010）和LSTM（Hochreiter和Schmidhuber, 1997；Graves, 2013）。最近，基于自注意力的Transformer网络带来了重要的改进，特别是在捕捉长距离依赖关系方面（Vaswani等人，2017；Radford等人，2018；Dai等人，2019）。

扩展。 语言模型在模型和数据集规模方面都有很长的扩展历史。Brants等人（2007）展示了使用在2万亿标记上训练的语言模型（产生了3000亿个n-gram）对机器翻译质量的益处。虽然这项工作依赖于一种简单的平滑技术，称为"Stupid Backoff"，但Heafield等人（2013）后来展示了如何将Kneser-Ney平滑扩展到Web规模数据。这使得能够在CommonCrawl的9750亿标记上训练5-gram模型，产生了一个包含5000亿n-gram的模型（Buck等人，2014）。Chelba等人（2013）引入了One Billion Word基准测试，这是一个大规模训练数据集，用于衡量语言模型的进展。

在神经语言模型的背景下，Jozefowicz等人（2016）通过将LSTM扩展到10亿参数，在Billion Word基准测试上获得了最先进的结果。之后，扩展Transformer模型导致了许多NLP任务的改进。著名的模型包括BERT（Devlin等人，2018）、GPT-2（Radford等人，2019）、Megatron-LM（Shoeybi等人，2019）和T5（Raffel等人，2020）。GPT-3（Brown等人，2020）的出现是一个重大突破，这是一个拥有1750亿参数的模型。这引发了一系列大型语言模型的开发，如Jurassic-1（Lieber等人，2021）、Megatron-Turing NLG（Smith等人，2022）、Gopher（Rae等人，2021）、Chinchilla（Hoffmann等人，2022）、PaLM（Chowdhery等人，2022）、OPT（Zhang等人，2022）和GLM（Zeng等人，2022）。Hestness等人（2017）和Rosenfeld等人（2019）研究了扩展对深度学习模型性能的影响，显示了模型和数据集大小与系统性能之间存在幂律关系。Kaplan等人（2020）专门为基于Transformer的语言模型推导了幂律关系，这些关系后来被Hoffmann等人（2022）通过在扩展数据集时调整学习率计划而进一步完善。最后，Wei等人（2022）研究了扩展对大型语言模型能力的影响。

8 结论

在本文中，我们介绍了一系列公开发布的语言模型，这些模型与最先进的基础模型具有竞争力。最值得注意的是，LLaMA-13B的性能优于GPT-3，同时尺寸小10倍以上，而LLaMA-65B与Chinchilla-70B和PaLM-540B相比具有竞争力。与以往研究不同，我们表明可以通过仅在公开可用的数据上训练来实现最先进的性能，而无需依赖专有数据集。我们希望向研究社区发布这些模型将加速大型语言模型的发展，并帮助改进其鲁棒性和缓解已知问题，如有害内容和偏见。此外，我们像Chung等人（2022）一样观察到，在指令上微调这些模型会带来有前途的结果，我们计划在未来的工作中进一步研究这一点。最后，由于我们看到随着规模扩大性能不断提高，我们计划在未来发布在更大预训练语料库上训练的更大模型。