Games101笔记

//大部分摘自阎令其Games101

一 图形学相关线性代数

点乘：

 

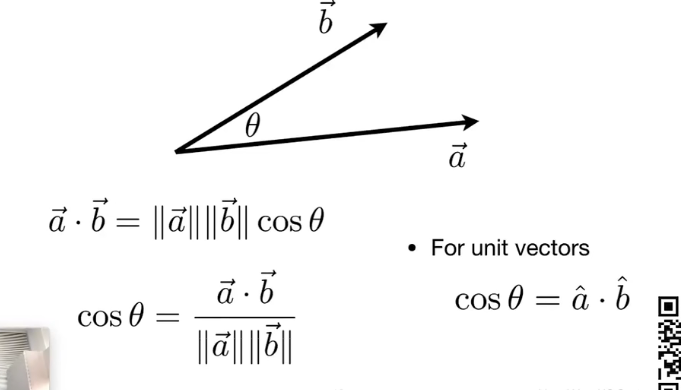
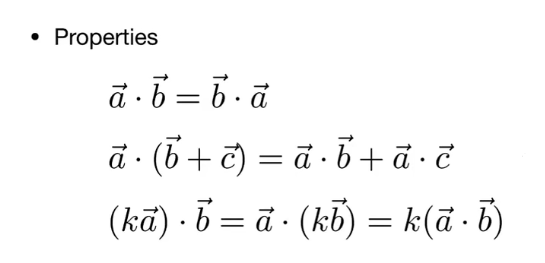
(默认是列向量)

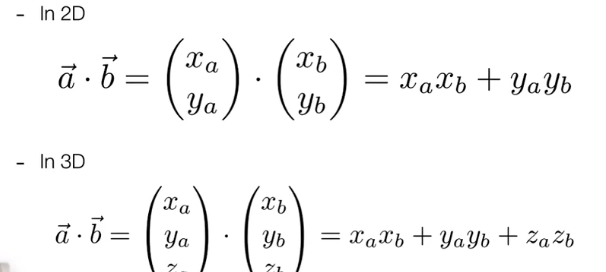
 单位向量时：cos=点积

叉乘

 

 

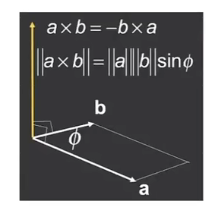
• 作用：判定左和右，内和外
• 右手定则：螺旋，锐角
• axb,手的旋转方向，反之类似

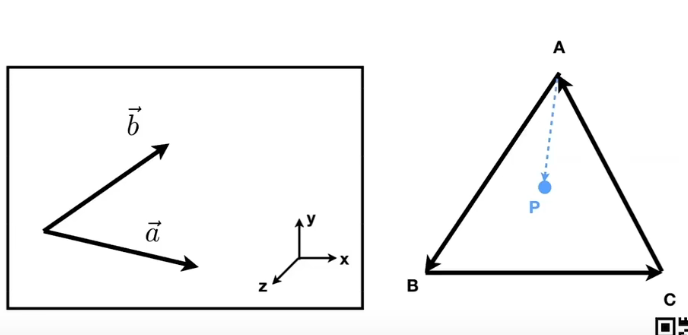
 判断内外；p点一直在左或右

 向量表示：

 矩阵：

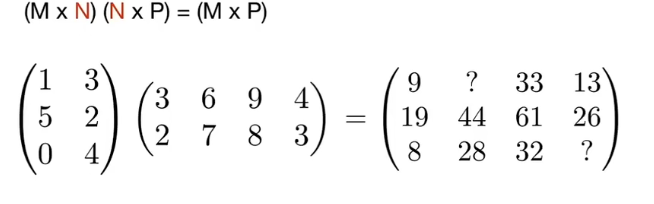
结果：例如（（1，2））A的第一行与B的第二行分别相乘求和

注：无交换律

转置：

 单位矩阵和矩阵的逆

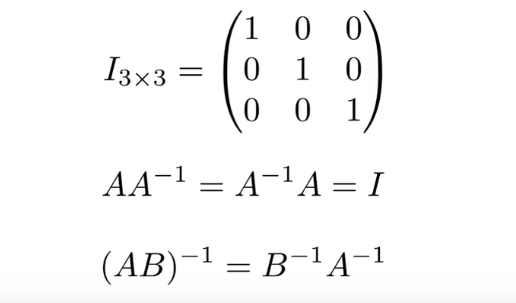
 向量的乘积变成矩阵的形式

 二 变换

Scale Matrix

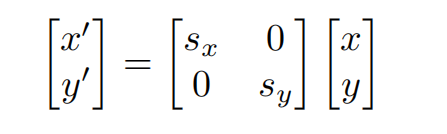
Reflflection（镜像） Matrix

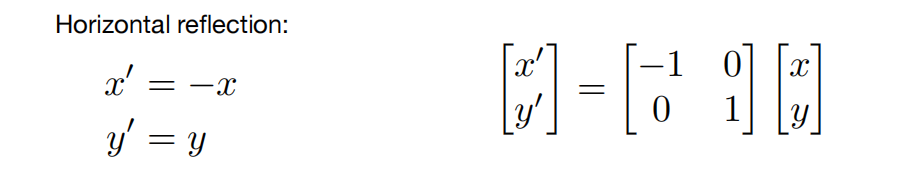
Shear（错切） Matrix

 Rotate(about the origin (0, 0), CCW by default)

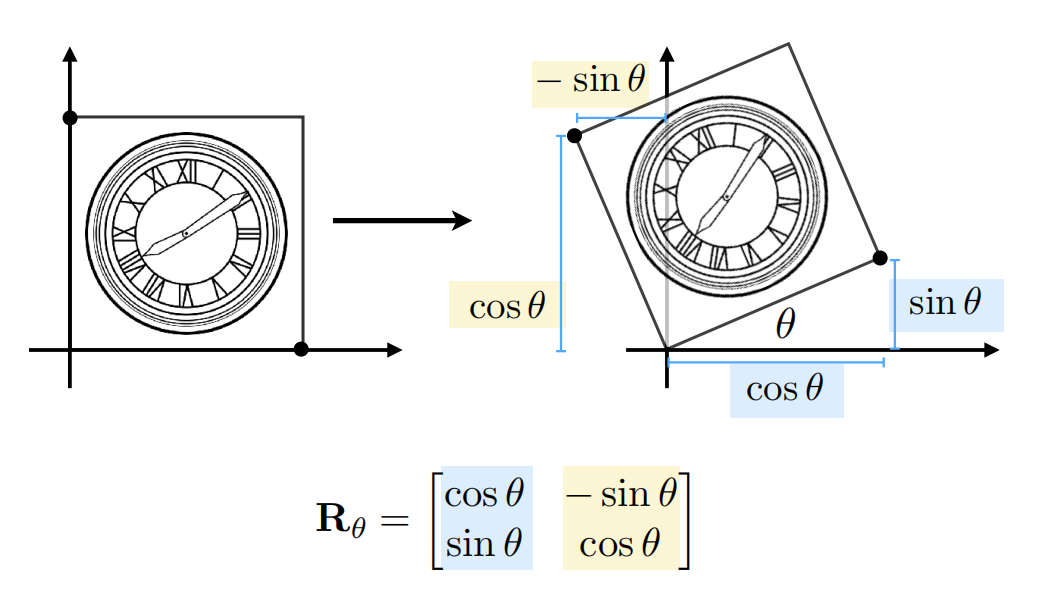
 以上统称线性变换

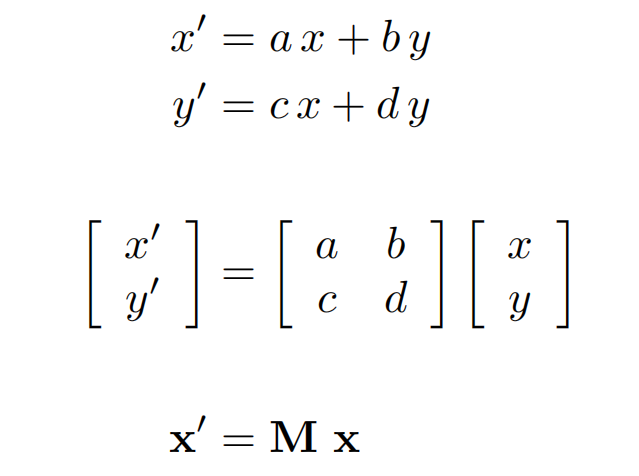
Translation（平移）

 

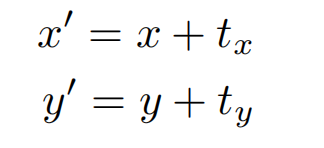
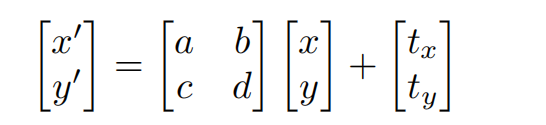
 齐次坐标

  

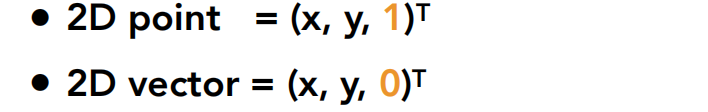
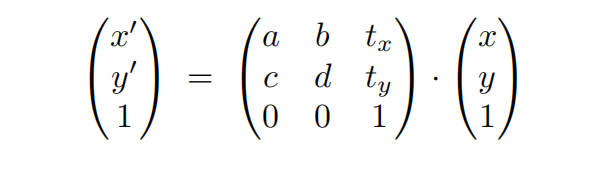
（左乘）

 （3D类似）

transformation cont（转换控制）

一个小性质：

 此性质为正交矩阵（逆等于转置）

3D变换

旋转

 y轴旋转不同的原因：zxx=y,

求任意方向的旋转：

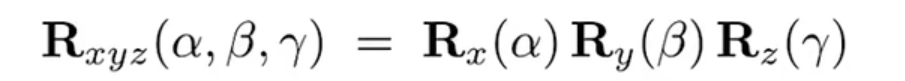
（角度为欧拉角）

罗德里格斯旋转公式（任意方向的旋转）

 

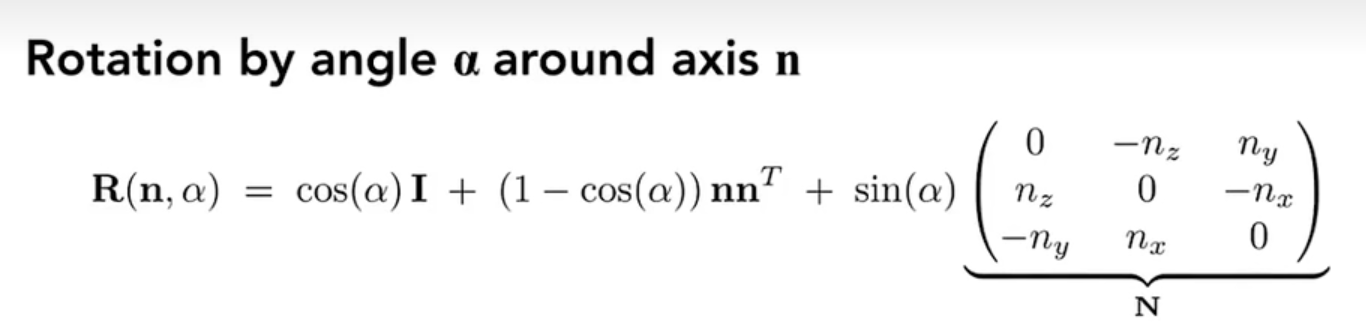
引入四元数的原因

 图形渲染到屏幕的大致流程（以摄像机拍照为例）

   人站位置（model 模型变换）

    调整摄像机位置（view 视图变换）

    拍照（projection 投影）

过程简述为MVP

 view 视图变换(对相机进行调整):

（约定俗成）

-位置，用向量 e 表示 -朝向，用向量 g 表示 -向上的方向，用向量 t 表示 

  

 处理过程：

 此变换也称作模型|视图变换

视图变换操作的对象是摄像机，场景中其它物体也同步进行变换（即摄像机转换为标准基的变换），以保持和摄像机的相对位置不变。模型变换和视图变换本质上都是对物体进行变换，也就是一个从 世界坐标系 ⇨ 摄像机坐标系 的过程，所以经常被放在一起被称作 “模型视图变换”。 

正交投影，透视投影

正交投影：

变换矩阵，首先移动（中心到原点），然后缩放（长度/宽度/高度到2）

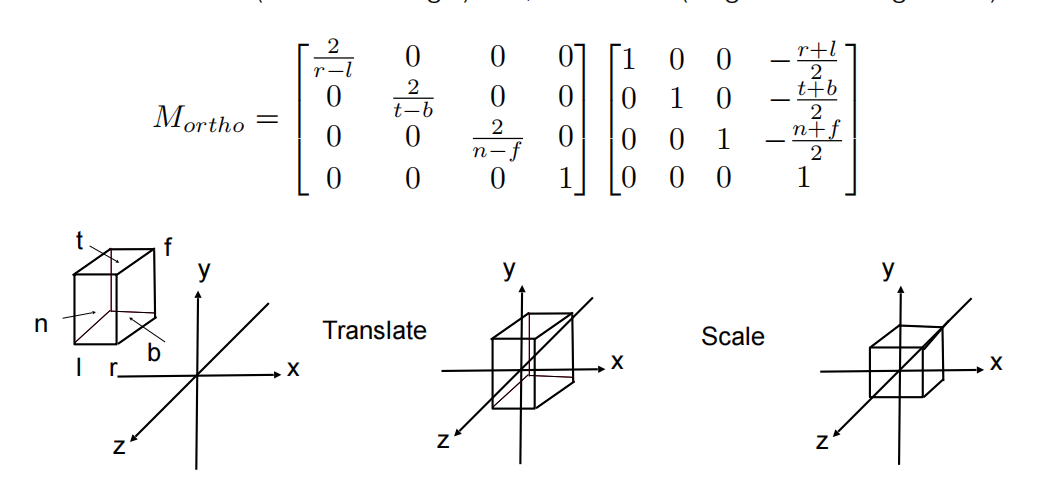
 透视投影：

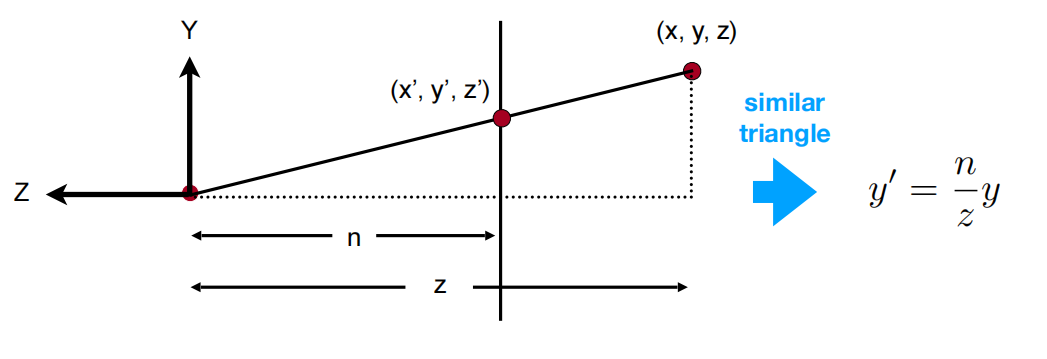
 在齐次坐标中，

 ——>

 ——>

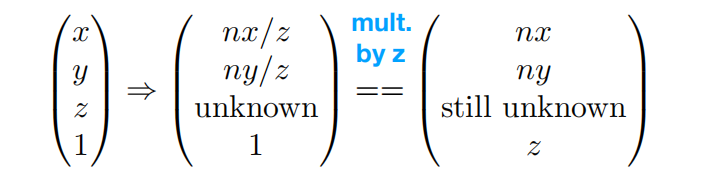
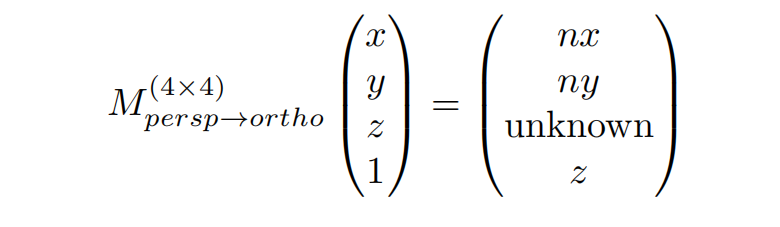
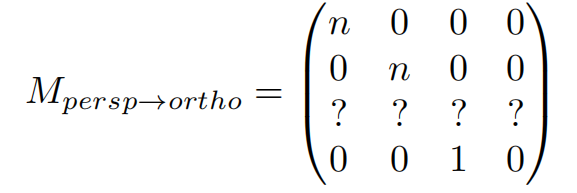
 求第三行：

 二 渲染

• 画家算法：从远到近依次渲染