数据结构十一、堆

堆的定义

        堆（heap），是一棵有着特殊性质的完全二叉树，对于树中的每一个节点，如果存在子树，那么该结点的权值大于等于（或小于等于）子树中所有节点的权值。如果根节点的权值大于等于子树的权值，称为大根堆；反之，称为小根堆。

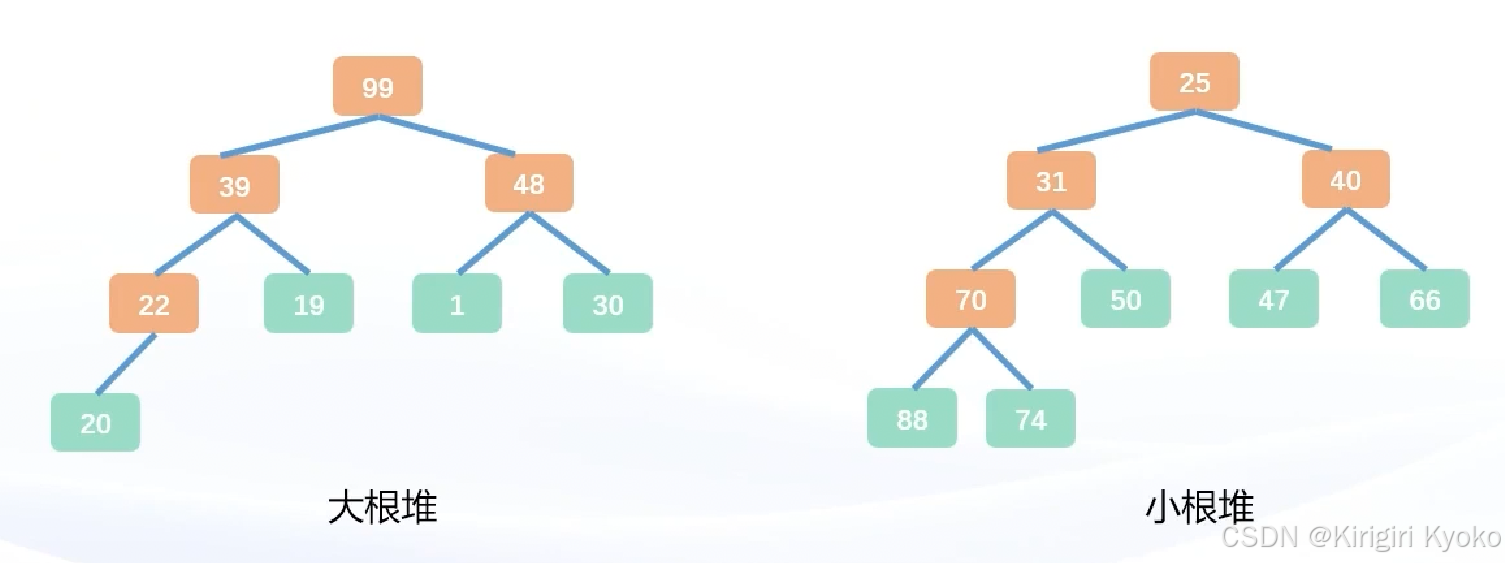
堆的核心操作

1、向上调整算法    

        向上调整算法用于向堆中插入元素。就是当堆中新来一个元素，放在末尾时，从这个节点开始，逐渐向上调整。算法流程：1、将该点与父节点的权值作比较，如果父节点的权值大，就与父亲交换  2、重复操作1，直到小于等于父节点的权值，或者换到根节点的位置为止。

代码实现：

#include <iostream>
using namespace std;

const int N = 1e5 + 10;
int n;
int heap[N];

// 向上调整算法
void up(int child)
{
	int parent = child / 2;
	while((heap[child] > heap[parent]) && (parent >= 1))
	{
		swap(heap[child], heap[parent]);
		child = parent;
		parent = child / 2;
	}
}

2、向下调整算法

        向下调整算法用于删除堆顶元素，或者堆排序中的建堆操作。就是从这个节点开始，逐渐向下调整。算法流程：1、找出左右孩子中权值最大的那一个，如果该点的权值比最大孩子的权值小，就交换。2、重复操作1，直到该点比两个孩子结点的权值都大，或者换到叶子结点为止。

#include <iostream>
using namespace std;

const int N = 1e5 + 10;
int n;
int heap[N];

// 向下调整算法
void down(int parent)
{
	int child = parent * 2;
	while(child <= n)
	{
		if((heap[child] < heap[child + 1]) && (child + 1 <= n))
		{
			child++;
		}
		swap(heap[parent], heap[child]);
		parent = child;
		child = parent * 2; 
	}
}

堆的模拟实现

        掌握好向上调整算法和向下调整算法之后，堆的实现就变得很简单了。

1、插入元素 

        把新元素放在最后一个位置，然后从最后一个位置开始执行一次向上调整算法。

#include <iostream>
using namespace std;

const int N = 1e5 + 10;
int n;
int heap[N];

// 向上调整算法
void up(int child)
{
	int parent = child / 2;
	while((heap[child] > heap[parent]) && (parent >= 1))
	{
		swap(heap[child], heap[parent]);
		child = parent;
		parent = child / 2;
	}
}

// 插入元素
void push(int x)
{
	heap[++n] = x;
	
	up(n);
}

2、删除堆顶元素

        1、将堆顶元素和最后一个元素交换，然后n--删除最后一个元素；

        2、从根节点开始执行一次向下调整算法。

#include <iostream>
using namespace std;

const int N = 1e5 + 10;
int n;
int heap[N];

// 向下调整算法
void down(int parent)
{
	int child = parent * 2;
	while(child <= n)
	{
		if((heap[child] < heap[child + 1]) && (child + 1 <= n))
		{
			child++;
		}
		swap(heap[parent], heap[child]);
		parent = child;
		child = parent * 2; 
	}
}

void pop()
{
	swap(heap[1], heap[n]);
	n--;
	
	down(1);
}

3、查询堆顶元素

        下标为1的位置的元素就是堆顶元素。

int top()
{
	return heap[1];
}

4、堆的大小

int size()
{
	return n;
}

小结

        那么以上就是堆的全部内容了，同样，C++的STL也提供了一个堆结构供我们使用，下一章我们再来重点介绍。