时变周期复合矢量MPC控制

永磁同步电机驱动的复合矢量模型预测控制与时变控制周期

摘要

本文提出了一种用于永磁同步电机（PMSM）驱动的具有时变控制周期的复合矢量模型预测控制（MPC）。首先，分析了模型预测控制方法中的传统矢量选择模式。然后，提出一种新的选择模式，该模式选取两个非零电压矢量作为最优电压矢量，并采用时变控制周期。与传统方法不同，所提出的方法能够调节控制周期以适应超出线性调制范围的参考电压矢量，从而改善稳态控制性能。与传统三矢量方法相比，由于减少了零电压矢量的使用，该方法在降低开关频率和抑制共模电压方面具有优势。最后，不同方法的实验对比结果验证了所提出方法的有效性。

索引术语 —模型预测控制，开关频率，过调制

---

一、引言

永磁同步电机（PMSM）具有结构简单、重量轻、效率高和可靠性高等优点，目前已被广泛应用于汽车驱动、轨道交通、航空航天等领域[1]。因此，针对PMSM的高性能控制方法成为研究热点，如矢量控制、直接转矩控制和模型预测控制（MPC）。近年来，由于模型预测控制具有设计简单、适应性强和良好的动态性能等优势，其在PMSM高性能控制中的应用受到广泛关注[2]‐[3]。

在传统模型预测控制中，根据系统的离散模型和逆变器的开关状态，通过成本函数预测电机在下一时刻需要施加的电压矢量（即逆变器开关状态）[4]。

然而，由于在传统MPC方法（单矢量法）中每个控制周期仅应用一个基本电压矢量，系统中存在较大的电流纹波。因此，为了抑制电流纹波并提高稳态性能，文献[5]‐[6]研究了包括双矢量和三矢量法在内的多矢量MPC方法。在双矢量MPC方法中，每个控制周期内应用两个基本电压矢量，这意味着两个基本电压矢量被用于逼近参考电压矢量[5]。早期的双矢量模型预测控制采用占空比控制[7]-[8]，即在一个控制周期内，通过非零矢量作用下的零矢量进行补偿，但零矢量对参考电压矢量的合成范围非常有限。文献中提出了广义双矢量模型预测控制[9]，即将两个任意电压矢量组合到成本函数中以选择最优组合。但由于组合数量较多，计算量大幅增加。因此，文献[10]提出通过选择复功率负共轭作为控制变量，实现广义双矢量法的复杂度降低。然而，由于固定控制周期的限制，双矢量法无法准确合成参考电压矢量。因此，尽管双矢量法相比单矢量模型预测控制方法具有更好的稳态性能，但仍存在较大的电流纹波。为了进一步提升模型预测控制的稳态性能，提出了三矢量选择方法[6]，即在每个控制周期内施加两个非零电压矢量和一个零电压矢量，从而能够准确合成参考电压矢量。在三矢量法中，电流纹波可被有效抑制。在[11]-[12]中，采用滑模观测器和卢恩伯格观测器来观测由模型失配和非模型动态引起的块状扰动，提高了对参数变化的鲁棒性，并减小了三矢量法的稳态电流误差。此外，为了降低计算复杂度，文献提出了一种结合死区控制和对称三矢量开关序列关系的控制方法[13]，该方法略微降低了开关频率。

另一方面，共模电压在电压源逆变器供电的PMSM控制系统[14]中普遍存在。共模电压可能产生电磁干扰和过大的漏电流，从而影响电机使用寿命[15]‐[16]。因此，在电机驱动中抑制共模电压非常必要。一些方法通过增加额外的硬件设备来实现共模电压的抑制[17]‐[18]。然而，应注意的是，由于增加了设备，控制系统的复杂性和设计成本也将增加。因此，提出了一些无需额外设备的模型预测控制方法，以进一步提高共模电压的抑制性能。在[19]中提出了一种模型预测控制方法，通过选择共模电压较小的候选电压矢量来降低共模电压。在[20]中，将共模电压作为新的控制目标加入成本函数，以减小共模电压。此外，在[21]‐[22]中提出了仅使用非零电压矢量的模型预测控制方法，通过优化矢量选择过程和矢量作用序列，可以获得满意的共模电压抑制性能。

然而，需要注意的是，尽管上述模型预测控制方法能够有效降低共模电压，但其稳态控制性能仍不理想，cannot同时获得。另一方面，在中高速阶段且电机在调制区域边缘附近运行时，尽管三-矢量模型预测控制方法具有令人满意的稳态控制性能，但高开关频率和共模电压不可避免。因此，本文提出一种具有时变周期的复合矢量模型预测控制方法，以进一步改善过-调制区域的稳态控制性能，同时降低共模电压。

本文的结构如下：第二节介绍了表面贴装式永磁同步电机（SPMSM）的数学模型和模型预测控制方法。接着在第三节中分析了多矢量选择MPC方法。在第四节中，为了同时减小电流纹波和共模电压，提出了一种具有时变周期的复合矢量模型预测控制方法。此外，在第五节中通过实验对比验证了所提出的方法的可行性。最后，第六节对本文进行了总结。

II. 永磁同步电机的传统模型预测电流控制

本文采用表面贴装式永磁同步电机（SPMSM）。由两电平三相电压源逆变器供电的SPMSM控制系统如图1所示。此外，SPMSM的模型预测电流控制（MPCC）方法如图2所示，主要包括以下部分：SPMSM的离散时间模型、延时补偿和成本函数最小化。

A. 表面贴装式永磁同步电机的离散时间模型

由于采用了SPMSM，d轴等效电感与同步旋转参考坐标系中的q轴电感相等（即Ld=Lq=L）。因此，SPMSM在同步旋转参考坐标系（dq坐标系）中的动态模型可描述为[23]

$$
\frac{d}{dt}
\begin{bmatrix}
i_d \
i_q
\end{bmatrix}
=
\begin{bmatrix}
-\frac{R}{L} & -\omega \
\omega & -\frac{R}{L}
\end{bmatrix}
\begin{bmatrix}
i_d \
i_q
\end{bmatrix}
+
\begin{bmatrix}
\frac{1}{L} & 0 \
0 & \frac{1}{L}
\end{bmatrix}
\begin{bmatrix}
u_d \
u_q
\end{bmatrix}
+
\begin{bmatrix}
0 \
-\frac{\omega \psi_f}{L}
\end{bmatrix}
\quad (1)
$$

为了获得下一个控制周期的电机电流，根据(1)式在同步旋转参考坐标系下建立了SPMSM的标准离散时间模型，表达如下

$$
\begin{bmatrix}
i_d(k+1) \
i_q(k+1)
\end{bmatrix}
=
\left(1 - \frac{T_s R}{L}\right)
\begin{bmatrix}
i_d(k) \
i_q(k)
\end{bmatrix}
+
\frac{T_s}{L}
\begin{bmatrix}
u_d(k) \
u_q(k)
\end{bmatrix}
+
\begin{bmatrix}
0 \
-\frac{T_s \omega(k) \psi_f}{L}
\end{bmatrix}
\quad (2)
$$

其中，ud(k)、uq(k) 和 id(k)、iq(k) 分别为第 k 个控制时刻的 dq-轴定子电压和 d-q-轴定子电流；id(k+1) 和 iq(k+1) 为第 (k+1) 个控制时刻的 d-q-轴定子电流；R 和 L 分别为定子电阻和电感；$\psi_f$ 为磁链；$\omega(k)$ 为第 (k) 个控制时刻的电角速度。

B. 单步-延时补偿

通常，数字实现中存在的单步延迟会影响实际应用中的动态和稳态性能，尤其是在低开关频率系统中。为了补偿单步延迟对控制性能的影响，通常采用单步预测方法[5]。因此，基于SPMSM的离散时间模型，可求得第(k+1)个时刻的电流作为补偿电流，如(2)所示。

C. 成本函数最小化

在传统模型预测电流控制方法中，控制目标是d轴和q轴定子电流。由于存在一步延迟补偿过程，成本函数中的定子电流需要基于第(k+1)时刻的电流再次进行预测，可按如下方式获得。

$$
\begin{bmatrix}
i_d(k+2) \
i_q(k+2)
\end{bmatrix}
=
\left(1 - \frac{T_s R}{L}\right)
\begin{bmatrix}
i_d(k+1) \
i_q(k+1)
\end{bmatrix}
+
\frac{T_s}{L}
\begin{bmatrix}
u_d(k) \
u_q(k)
\end{bmatrix}
+
\begin{bmatrix}
0 \
-\frac{T_s \omega(k) \psi_f}{L}
\end{bmatrix}
\quad (3)
$$

对于一个两电平三相电压源逆变器，它可以生成八个电压矢量，对应在第 (k+2)个时刻的八组预测电流。然后，使用成本函数(4)来选择具有成本函数最小值的电压矢量作为最优电压矢量。

$$
g = [i_d^ - i_d(k+2)]^2 + [i_q^ - i_q(k+2)]^2 \quad (4)
$$

然后，在每个控制周期将所选择的最优电压矢量施加到电机上。这意味着一个控制周期施加一个电压矢量，这在本文中称为单-矢量选择模式。

三、传统模型预测控制的矢量选择分析

A. 单矢量选择模式

根据上述[24]‐[26]所描述的单矢量选择过程，等效于从八个基本电压矢量中选择一个最接近参考电压矢量的电压矢量的过程。换句话说，在单矢量选择模式下，可以通过直接比较参考电压矢量和八个候选电压矢量来实现电压矢量选择。因此，在单矢量选择模式下，每个固定控制周期内仅应用一个电压矢量，具有低开关频率的优点；然而，由于最优电压矢量的单一构成，无法准确合成参考电压矢量，这意味着在单矢量选择模式下控制系统存在较大的稳态误差。

为了更好地比较单矢量选择模式下的参考电压矢量与所选最优电压矢量，假设参考电压矢量位于第一扇区，如图3(a)所示，其中uref表示参考电压矢量，uopt表示所选的最优电压矢量，∆uref表示电压误差。可以看出，参考电压矢量与最优电压矢量之间存在较大的电压误差(i.e.,∆uref），这将导致较大的电流纹波，如图3(b)所示。

B. 多矢量选择模式

与单矢量选择模式相比，采用多矢量选择模式的模型预测控制具有更好的控制性能。多矢量选择模式可分为两种类型，即双矢量模式和三矢量模式。

在双矢量模式下，每个固定控制周期内选择一个非零电压矢量和一个零矢量，或两个非零电压矢量作为最优电压矢量，以逼近参考电压矢量。双矢量选择模式下参考电压矢量与最优电压矢量之间的关系如图4所示。由于每个开关周期内施加了两个电压矢量，与单矢量选择模式相比，最优电压矢量可以更接近参考电压矢量。因此，双矢量选择模式的电流纹波低于单矢量选择模式，如图4(b)所示。然而，在控制周期固定的情况下，双矢量选择模式无法准确合成参考电压矢量，这意味着仍然存在电压误差。

矢量分布 (b) current所选矢量引起的误差)

在三矢量模式下，每个固定控制周期内选择两个非零电压矢量和一个零矢量作为最优电压矢量，以逼近参考电压矢量。参考电压矢量与 optimal电压矢量在三矢量选择模式下的关系如图5所示。由于在每个控制周期内施加了三个电压矢量，因此可以精确合成参考电压矢量。这意味着参考电压矢量与最优电压矢量之间的电压误差可以被消除，稳态控制性能相比单矢量选择模式和双矢量选择模式得到改善。然而需要注意的是，由于每个控制周期内电压矢量数量的增加，三矢量选择模式具有更高的开关频率。

为了比较单矢量选择模式、双矢量选择模式和三矢量选择模式下的差异，图6和图7展示了在固定控制周期下三种模式的最优电压矢量有效范围及其开关序列。

从图7可以看出，单向量选择 mode和双向量选择 mode的开关动作较少（低开关频率）。然而，由于在一个控制周期内所施加的电压矢量数量受限，只能准确合成调制区域边缘的参考电压矢量，而调制区域内部大多数的参考电压矢量无法通过单矢量选择模式 mode和双矢量选择 mode合成，如图6(a)和(b)所示。因此，稳态控制性能不理想。也就是说，尽管单矢量选择模式和双矢量选择模式的开关频率较低，但电流纹波较大是不可避免的。然而，在三矢量选择模式下，调制区域边缘和内部的所有参考电压矢量都可以被合成，如图6(c)所示。但开关频率显著增加。

上述分析表明，在模型预测控制方法中，开关频率与稳态控制性能是相互矛盾的。获得满意的稳态性能的代价是更高的开关频率。因此，有必要开发一种不同的模型预测控制方法，能够在较低开关频率下实现令人满意的稳态控制性能。

IV. 所提出的复合矢量模型预测控制

在本节中，提出了一种复合矢量模型预测控制方法。在所提出的方法中，选择两个非零电压矢量作为最优电压矢量，并利用它们的持续时间来确定控制周期。这意味着所提出的方法的控制周期不是固定的，而是时变的，以精确合成参考电压矢量。复合矢量模型预测控制方法的控制方案如图8所示，主要由四个部分组成：参考电压矢量计算、扇区确定、最优电压矢量选择以及时变控制周期（Ts）的计算。

永磁同步电机驱动的复合矢量模型预测控制与时变控制周期

A. 参考电压矢量计算与扇区确定

该方法采用基于参考电压矢量的快速矢量选择方法，以降低MPC[5]的计算负担。参考电压矢量根据电流无差拍控制原理计算得到。因此，根据电压模型(1)，参考电压矢量可描述为

$$
\begin{bmatrix}
u_{dref} \
u_{qref}
\end{bmatrix}
=
\begin{bmatrix}
R i_d - \omega L i_q \
R i_q + \omega L i_d + \omega \psi_f
\end{bmatrix}
+
\frac{T_s}{2}
\begin{bmatrix}
\frac{d i_d}{dt} \
\frac{d i_q}{dt}
\end{bmatrix}
\quad (5)
$$

其中，udref、uqref分别表示d轴、q轴参考电压矢量，idref、iqref分别表示d轴、q轴参考电流。id、iq分别表示d轴、q轴采样电流。

然后，根据(5)，参考电压矢量在αβ坐标系中可通过克拉克变换计算如下

$$
\begin{cases}
u_{\alpha ref} = u_{dref} \cos(\theta) - u_{qref} \sin(\theta) \
u_{\beta ref} = u_{dref} \sin(\theta) + u_{qref} \cos(\theta)
\end{cases}
\quad (6)
$$

接下来，参考电压矢量的位置角（θ）可以如下获得

$$
\theta = \arctan\left(\frac{u_{\beta ref}}{u_{\alpha ref}}\right) \quad (7)
$$

根据参考电压的位置角，可以得到参考电压矢量所在的扇区，如图9所示。

B. 最优电压矢量确定

一个两电平三相电压源逆变器产生八个可行电压矢量，包括六个非零电压矢量和两个零电压矢量，如图9所示。每个电压矢量将产生不同的共模电压（CMV）。在永磁同步电机控制系统中，共模电压定义为永磁同步电机中性点与逆变器直流母线中点之间的电位（Ucm），如图1所示。因此，该共模电压可通过以下公式[19]获得。

$$
U_{cm} = \frac{1}{3}(u_{ao} + u_{bo} + u_{co}) \quad (8)
$$

根据(10)，由八个电压矢量产生的共模电压列于表I中。从该表可以看出，当电压矢量为非零电压矢量时，逆变器的共模电压为±Udc/6；当电压矢量为零电压矢量时，逆变器的最大共模电压为±Udc/2。换句话说，与非零电压矢量相比，零电压矢量具有更大的共模电压幅值。需要注意的是，较大的共模电压将导致较大的漏电流，从而引起电磁干扰并缩短电机使用寿命。因此，在永磁同步电机的模型预测控制系统中，电压矢量的合理选择对控制性能至关重要。

电压矢量和开关状态	共模电压（Ucm）
非零电压矢量 (100),(010),(001)	$-U_{dc}/6$
非零电压矢量 (110),(011),(101)	$U_{dc}/6$
零电压矢量 (000)	$-U_{dc}/2$
零电压矢量 (111)	$U_{dc}/2$

本文中，为了实现高性能的稳态控制并同时限制共模电压（CMV）水平，提出了一种不同的电压矢量选择模式。与传统矢量选择模式（单矢量选择模式、双矢量选择模式和三矢量选择模式）不同，该方法选择两个非零电压矢量作为最优电压矢量，相较于零电压矢量，其共模电压更低。

具体地，根据位置角（7），可以确定参考电压矢量的扇区；由于每个扇区包含两个非零电压矢量，因此可以容易地获得距离参考电压矢量最近的两个最优电压矢量。假设参考电压矢量位于第一扇区，如图9所示，则应选择电压矢量 u1 和 u2 作为最优电压矢量。类似地，当参考电压矢量位于其他扇区时，也可选择距离该参考电压矢量最近的两个非零电压矢量。由于两个相邻非零电压矢量产生的共模电压具有相同幅值但方向相反；因此，使用两个相邻非零电压矢量而不使用零电压矢量可有效抑制共模电压的产生。

然后，参考电压矢量可以通过选定的两个非零电压矢量合成，可表示为

$$
\mathbf{u}_s = \frac{t_i}{T_s} \mathbf{u}_i + \frac{t_j}{T_s} \mathbf{u}_j \quad (9)
$$

其中；；us表示参考电压矢量，ui和uj分别表示两个非零电压矢量；Ts表示控制周期；
$\mathbf{u} = [u_d, u_q]^T$，$\mathbf{u} {ij} = [u {d,ij}, u_{q,ij}]^T$
ti 和 tj 分别表示两个非零电压矢量的持续时间。

C. 最优电压矢量的持续时间计算及时变控制周期确定

为了实现无差拍电流跟踪，合成电流方程可表示为

$$
i_s^* = i_s(k+1) + s_i t_i + s_j t_j \quad (10)
$$

其中;; si和 sj分别表示所选的两个非零电压矢量的电流斜率（即，dis/dt）； is(k+1) 表示一步延迟补偿电流。根据(1)，由最优电压矢量产生的d轴和q轴电流斜率可表示为(11)。

$$
\begin{cases}
s_{d,i(j)} = \frac{1}{L}(u_{d,i(j)} - R i_d + \omega L i_q) \
s_{q,i(j)} = \frac{1}{L}(u_{q,i(j)} - R i_q - \omega L i_d - \omega \psi_f)
\end{cases}
\quad (11)
$$

然后，将(11)代入(10)，得到两个非零电压矢量的持续时间

$$
\begin{cases}
t_i = \frac{i_q^ - i_q(k+1) - s_{q,j} t_j}{s_{q,i} - s_{q,j}} \
t_j = \frac{i_d^ - i_d(k+1) - s_{d,i} t_i}{s_{d,j} - s_{d,i}}
\end{cases}
\quad (12)
$$

为了确保参考电压矢量的精确合成，该方法中控制周期由两个非零电压矢量的持续时间确定，这表示控制周期是时变的。根据(12)，这个时变控制周期可以表示为

$$
T_s’ = t_i + t_j \quad (13)
$$

其中Ts’表示时变控制周期，其随两个非零电压矢量的持续时间而变化。

时变控制周期具有最小时间限制，即程序执行时间（TN）。为了确保控制程序的完整执行，时变控制周期不能小于程序执行周期（即）。
$T_s’ \geq T_N$

当计算的控制周期小于程序执行时间（即）时，添加零电压矢量以补偿剩余时间，确保计算的控制周期等于程序执行时间。该过程等效于三矢量选择模式。此外，当计算的控制周期等于程序执行时间（即）时，每个控制周期Ts包含两个非零电压矢量（和）或一个非零电压矢量（或），分别等效于双矢量选择模式和单矢量选择模式。上述三种模式的控制周期设为固定控制周期，即。
$T_s’ < T_N$
$T_s’ = T_N$
$t_i \neq 0, t_j \neq 0$ 或 $t_i = 0, t_j = 0$
$T_s = T_N$

另一方面，当计算出的控制周期大于程序执行周期时（即），这意味着参考电压超出了线性调制区域（即处于过调制状态）。因此，有必要分析所提出的方法在过调制状态下的控制性能。
$T_s’ > T_N$

在恒定控制周期（即，）中，传统比例分配方法（14）只能选择与参考电压同方向的电压矢量，而非最接近参考电压的电压矢量，如图10(a)所示。
$T_s’$

$$
\begin{cases}
t_i = \frac{t_i’}{t_i’ + t_j’} T_s \
t_j = \frac{t_j’}{t_i’ + t_j’} T_s
\end{cases}
\quad (14)
$$

因此，在[27]中提出了一种模型预测控制的优化过调制方法。该方法将过调制区域划分为三个部分，并根据参考电压所处的区域选择最接近参考电压的电压矢量。然而，由于参考电压矢量与矢量作用时间及其周期相关，如式(9)所示，这种采用固定控制周期的方法在过调制条件下无法准确合成电压矢量，而只能选择位于六边形边缘且最接近参考电压矢量的矢量作用于电流预测，如图10(b)所示。这意味着在固定控制周期和过调制条件下，参考电压矢量与所选电压矢量之间存在电压误差。

然而，与上述方法不同，所提出的方法可以通过改变控制周期来合成线性调制区域之外的参考电压，如图10(c)所示。该过程可称为变控制周期双矢量选择模式。另一方面，如果计算出的非零电压矢量的持续时间为零（即），这意味着参考电压矢量与基本电压矢量重合。因此，在一个控制周期内仅需使用一个基本电压矢量
$t_i = 0$ 或 $t_j = 0$

控制周期足以跟踪参考电压矢量，然后变控制周期双矢量选择模式切换为变控制周期单矢量选择模式。上述两种模式的控制周期均设为可变控制周期，即。
$T_s = T_s’$

总之，根据计算出的控制周期（即）与程序执行时间（即）之间的关系，具体动作模式分配如表II所示。
$T_s’$ $T_N$

$T_s’ < T_N$	固定控制周期 ($T_s = T_N$)	三矢量选择模式	$t_i \neq 0$ and $t_j \neq 0$
$T_s’ = T_N$	固定控制周期 ($T_s = T_N$)	双矢量选择模式	$t_i \neq 0$ and $t_j \neq 0$
		单矢量选择模式	$t_i = 0$ or $t_j = 0$
$T_s’ > T_N$	变量控制周期 ($T_s = T_s’$)	双矢量选择模式（变周期）	$t_i \neq 0$ and $t_j \neq 0$
		单矢量选择模式（变周期）	$t_i = 0$ or $t_j = 0$

V. 实验结果

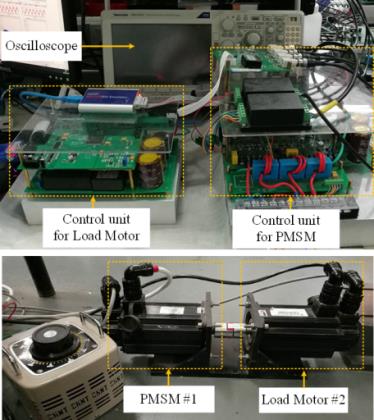
为了验证所提出的方法的控制性能，本节给出了传统三矢量MPC方法、双矢量MPC方法和所提出的方法的实验对比结果。The永磁同步电机的参数列于表III中，测试平台如图11所示。

电机参数/符号	值
直流母线电压，Udc	310 V
极对数，p	2
定子相电阻，R	1.59 Ω
d轴和q轴电感，L	6.6 mH
磁链，ψf	0.24 Wb
系统功率，P0	1.25 kW
额定转矩，TeN	6 N·m
额定速度，nN	2000 rpm

本文所采用的数字信号处理器为TI-DSP28335，其时钟频率为150兆赫，即时钟周期为1/150微秒。因此，所提出的方法的程序执行时间（TN）可通过时钟周期数进行测量。本文中，所提出的方法的程序执行时间为55微秒，即该方法的时变控制周期的最小限制时间为55微秒（亦即本文中所提出的方法的最大控制频率为18千赫）。为了公平地比较三矢量MPC方法、双矢量MPC方法与所提出的方法，本文将三种方法的控制频率均选为18千赫。

A. 稳态性能

四种方法在4N·m负载和2000转/分钟的额定速度下的比较结果如图12所示。四种方法在不同速度条件下的比较结果如图13所示。从结果可以看出，三矢量法和所提出的方法具有相似的稳态控制性能，而在相同控制频率下，单矢量法和双矢量法的性能较差。

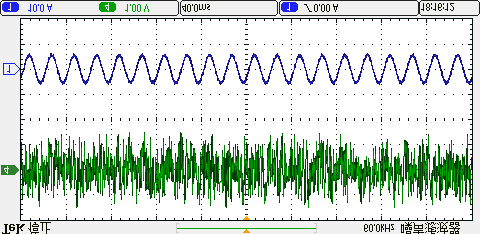
B. 动态性能

为了测试动态响应，给出了四种方法在速度为500rpm时负载转矩从2N·m阶跃到4N·m的动态性能，如图14所示。从结果可以看出，所提出的方法的动态性能与传统方法相似。

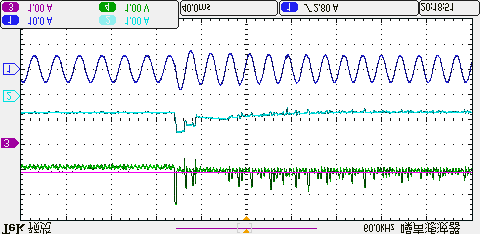
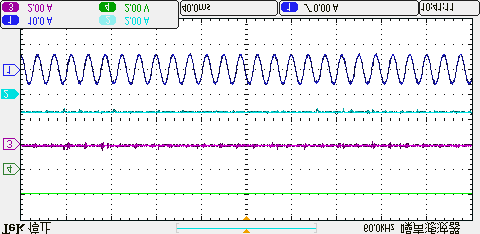
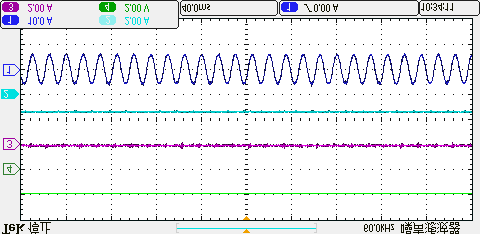
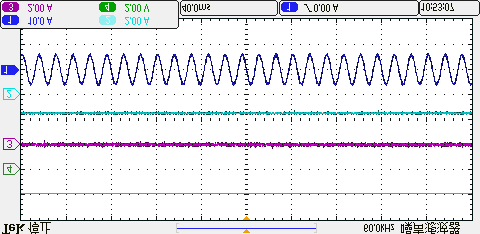
C. 共模电压抑制

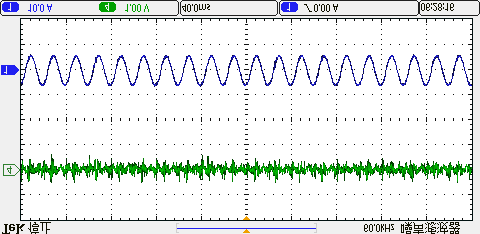
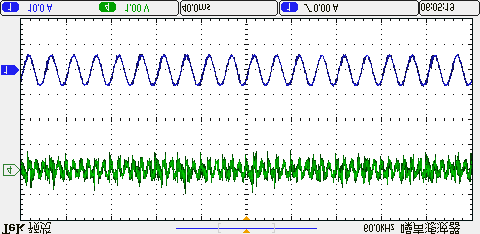
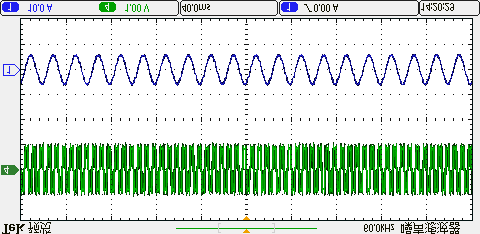
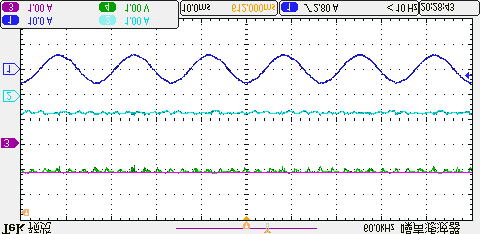
四种方法在相同平均开关频率下产生的共模电压的实验结果如图15所示。可以看出，传统方法未限制零电压矢量的作用时间，因此共模电压的波动幅度相对较大。而本文所提出的方法通过调整控制周期，可利用两个非零电压矢量进行电压矢量合成，在不使用零电压矢量的情况下将共模电压限制在±udc/6以内。因此，与传统方法相比，共模电压得到了进一步抑制。

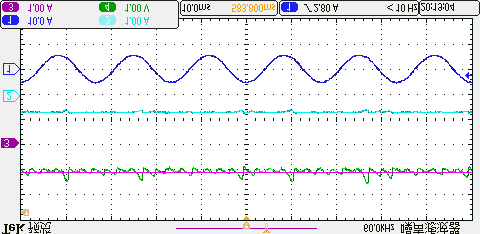所提出的方法，(b) 三矢量法，(c) 双矢量法，(d) 单矢量法。)

D. 过调制测试

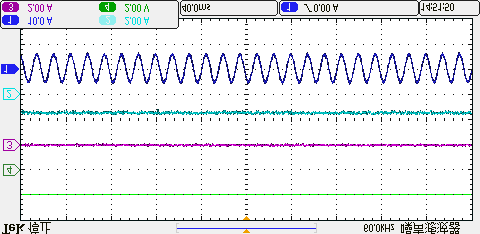
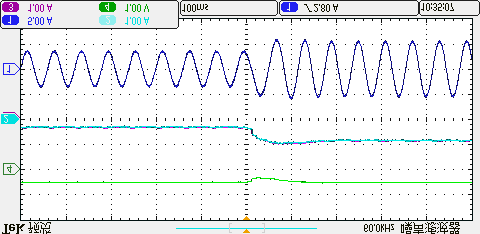
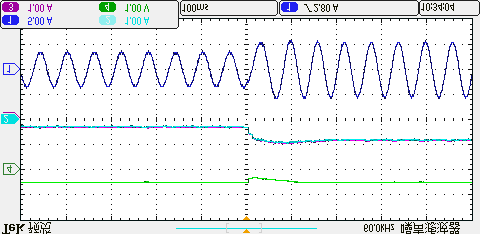
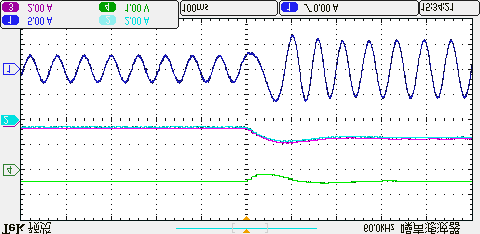
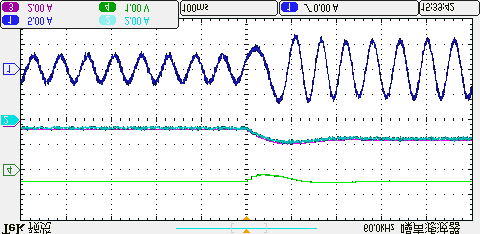
为了验证该方法在过调制区域的优越性，将直流母线电压降低至欠压状态。本文中直流母线电压设为250伏特（即Udc=250V）。图16展示了电机转速从1500转/分钟升至1800转/分钟时所提出的方法与三矢量法的动态结果，以及在达到1800转/分钟、负载为4N·m时的稳态结果。红色实线的值为所提出方法的最小控制周期（TN= 55us）（同时也是三矢量法的固定控制周期）。绿色通道表示两个非零电压矢量的计算作用时间，即ti+tj=Ts’。由图16(a)可以看出，当电机运行在1500转/分钟速度下时，在所提出方法的控制下，Ts’与TN之间的关系为ti+tj=Ts’<TN ，两个非零电压矢量作用时间为Ts’，剩余时间通过零矢量补偿直至TN= 55us；这意味着在ti+tj=Ts’ TN ，这意味着参考电压已超出传统线性调制区。因此，为了准确跟踪处于过调制区域的参考电压，所提出方法的控制周期开始根据计算作用时间进行调整。

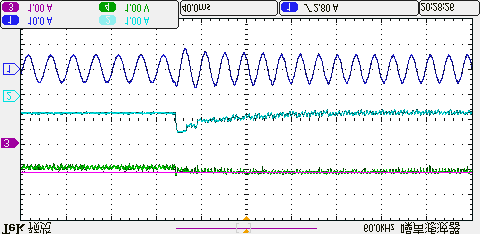所提出方法的动态结果 (b) 所提出方法在1800转/分时的稳态结果 (c) 三矢量法的动态结果 (d) 三矢量法在1800转/分时的稳态结果。)

从图16(a)和(c)可以明显看出，所提出的方法的动态性能与传统三矢量方法相似。然而，所提出的方法的计算控制周期是变化的，因此参考电压可以在过调制区域被准确合成，而传统三矢量方法只能通过减少零矢量的作用时间来降低过调制区域中的参考电压合成误差。因此，从图16(b)和(d)可以看出，当速度稳定在1800转/分钟时，所提出的方法的q轴电流和a相电流总谐波失真低于三矢量法。上述结果表明，所提出的方法在过调制区域的稳态性能优于传统方法。

为了进一步比较四种方法在过调制区域的性能，图17给出了不同电机转速下四种方法的开关频率对比。可以看出，尽管双矢量法和单矢量法的电流总谐波失真较高，但其开关频率相比三矢量法和所提出的方法更低。另一方面，当电机转速达到中高速时，参考电压矢量进入过调制区域。在所提出的方法中，控制周期被延长，从而将选择模式从三矢量选择模式转变为变控制周期双矢量选择模式，进而能够合成准确的参考电压，同时系统的开关频率逐步降低。然而，在过调制区域，传统三矢量方法仅减少零矢量的使用，因此合成的电压矢量只能位于调制区域的边缘，开关频率仅略有降低。因此，所提出的方法在降低过调制区域开关频率方面具有明显优势。

此外，为了进一步比较在相同开关频率条件下不同方法的稳态控制性能，以所提出的方法在不同转速下的开关频率作为参考（基于图17中所提出方法的开关频率），控制频率其他方法在不同转速下的参数已进行调整。这被视为不同控制方法进行比较时的通用做法和标准[28]。在相同开关频率下，不同方法的电流总谐波失真比较如图18所示。由于单矢量法的开关频率相对较低，无法将其开关频率提高到与所提出的方法相同的水平，因此图18仅展示了双矢量法、三矢量法和所提出的方法的电流总谐波失真对比。

可以看出，在整个速度阶段，在相同开关频率条件下，三矢量MPC方法和所提出的方法相比双矢量MPC方法具有更低的电流总谐波失真；另一方面，将所提出的方法与三矢量MPC方法进行比较可知，在低速阶段，三矢量MPC方法和所提出的方法具有相似的稳态控制性能；然而，在中高速阶段（过调制区域），所提出的方法具有明显优势。

VI. 结论

本文提出了一种具有时变控制周期的复合矢量MPC方法，并进行了实验验证。结果表明，与传统MPC方法相比，所提出的方法通过合理选择电压矢量，能有效抑制共模电压的产生。此外，本文中的控制周期可进行调整，以适应参考电压矢量位于线性调制范围之外的情况，并减少零电压矢量的使用。因此，与传统方法相比，所提出的方法在中高速阶段能够更有效地合成调制边界和过调制区域的电压矢量，从而提高系统的稳态性能。