最大流最小割定理是网络流理论的关键定理，指出在网络中最大流的值等于最小割的容量。该定理通过割的概念，即网络顶点的划分，来解释流的特性，并且在图论中有广泛应用。最小割是所有割中容量最小的一个，而最大流是在网络中能实现的最大流量。定理表明，找到最大流等价于找到最小割，这对解决实际问题有着重要意义。
附录J 最大流最小割定理
最大流最小割定理（max-flow min-cut the-orem）是网络流理论中的重要定理。它是图论中的一个核心定理。
关于判定流的最大性的定理，任何网络中最大流的流量等于最小割的容量，简称为最大流最小割定理。它描述了最大流的特征，图论中的很多结果在适当选择网络后，都可以由这个定理推出。
割：是网络中顶点的划分，它把网络中的所有顶点划分成S和T两个集合，源点s∈S，汇点t∈T，记为CUT（S，T）。
如图J-1所示，源点为s，汇点为t。有一条切割线把图中的结点切割成了两部分S={ s，v1，v2}，T={ v3，v4，t}。
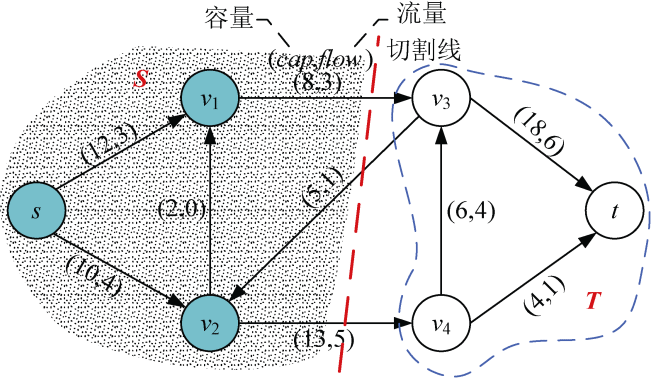
图J-1 割
割的净流量f（S，T）：切割线切中的边中，从S到T的边的流量减去从T到S的边
订阅专栏 解锁全文
扫一扫
4017
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
