
一前一后俩指针依次扫描和删除,free aim
//设,结构体为
typedef struct LNode{
int data;
struct LNode *next;
}LNode,*LinkLisst
void delete(LinkList &l,int x){
LNode *p=l->next;
LNode *q=l;
while(p!=null){
if(p->data==x){
pre->next=p->next;
free(p);
p=pre->next;
}else{
p=p->next;
pre=pre->next;
}
}
}

归并思路
//最简单的思路就是归并
void answer(int a[],int b[],int &c[]){
int i=0;
int t=0;
int m=0;
while(i<a.length&&t<b.length){
if(a[i]>=b[t]){
c[m]=a[i];
i++;
m++;
}
else{
c[m]=b[t];
m++;
t++;
}
}
if(i==a.length){
for(t;t<b.length;t++){
c[m]=b[t];
m++;
}
}
else{
for(i;i<a.length;i++){
c[m]=a[i];
m++;
}
}
}

尾插法与头插法
尾插是正序
头插法是逆序
void swap(SqList a[]){
int mid=a.length/2;
int tempt;
for(int i=0;i<mid;i++){
tempt=a[a.length-i-1];
a[a.length-i-1]=a[i];
a[i]=a[a.length-i-1];
}
}

删除一个元素,思路有很多,目前简单的是
指针删除法,两个指针,一个表示插入的位置和筛选数组最后的一个,一个对遇到要删除的东西进行跳跃
如果第一个指针小于长度,则可知删除成功,让长度等于其
//算法分析:顺序表中删除元素,则要考虑移动的问题,同时又说时间复杂度为
//o(n),则想到直接插入排序,可以对其进行变种,eg:12345,aim是3,则1/2345
//12/345,124/(4)5.指针调一下
void answer(SqList &a[],int e);
int i=0;
int mid;
for(int j=0;j<l.length;j++){
if(a[j]!=x){
a[i]=a[j];
i++;
}
}//第一趟循环完成后,i会小于或者等于j
if(i<l.length-1){
for(i;i<l.length;i++){
a[i]=0;
}
//或者,设length是他有多少个数据的长度,不是数组长度
//a.length=i;
}
//还有一种思路,在视频里面,简单来说就是前面有几个x就移动几个位子

是对上一个提的升级,变化的只有特殊值
思路很简单,一个是外部的i 一个是for j循环,要理解
bool answer(SqList &a[],int s,int t);
if(s>=t){
printf("s或t不合理")
retrun false;
}
if(a==null){
printf("表空")
retrun false;
}
int i=0;
int mid;
for(int j=0;j<l.length;j++){
if(a[j]<s||a[j]>t){
a[i]=a[j];
i++;
}
}//第一趟循环完成后,i会小于或者等于j
a.length=i;
}

//分析:没有明说时间和空间的要求,那么有一种不在乎空间的方法,申请一个
//长度是L最大值的数组,然后进行标记运算
void delete(SqList &a[]){
int max=a[0];
for(int i=0;i<a.length;i++){
if(a[i]>max)
m=a[i];
}
int c[max];
int tempt=0;
for(int i=0;i<a.Length;i++){
if(c[a[i]]==0){
a[tempt]=a[i];
tempt++;
c[a[i]]=1;
}
}
a.length=tempt;
}

局部逆置,逆置的算法就是中间除2然后交换
void swap(SqList &a[],int b,int u){
int mid=(b+u)/2;
int tempt;
for(int i=b-1;i<mid;i++){
tempt=a[a.length-i-1];
a[a.length-i-1]=a[i];
a[i]=a[a.length-i-1];
}
}
void MaxSwap(SqList &b[]){
swap(b,0,a.length);
swap(b,0,n);
swap(b,n+1,m);
}

设置一个最小值的指针
void answer(LinkList &L){
LNode *p=L->next;
LNode *pre=L;
LNode *temptpre=pre;
LNode *tempt=p;
int min=p->data;
while(p!=null){
if(p->data<min){
temptpre=pre;
tempt=p;
min=p->data;
}
p=p->next;
pre=pre->next;
}
LNode *u=tempt;
temptpre->next=tempt->next;
free(u);
}

void insert(LinkList &L,int a){
LNode *p=(LNode *)malloc(sizeof(LNode));
p->next=null;
p->data=a;
LNode *q=L->next;
L->next=p;
p->next=q;
}

void insert(LinkList &L,int a){
LNode *p=(LNode *)malloc(sizeof(LNode));
p->data=a;
p->next=null;
LNode *q=L->next;
int i=q->data;
p->next=q;
L->next=p;
p->data=i;
q->data=a;
}

//头插法
void sort(LinkList &L){
LNode *p=L->next->next;
LNode *pre=L->next;
while(p!=null){
pre->next=p->next;
p->next=L->next;
L->next=p;
p=pre->next;
}
}

bool delete(LinkList &L,int a,int b){
if(a>b){
return false;
}
LNode *p=L->next;
LNode *pre=L;
while(p!=null){
if(p->data>=a&&p->data<=b){
pre->next=p->next;
free(p);
p=pre->next;
}else{
p=p->next;
pre=Pre->next;
}
}

//分析:信息给的太少了,但是没有限制条件,则思路是,申请一个数组,把访问的结点的值
//打上标记
typedef strcut List{
int data;
LNode *p;
}List;
bool find(LinkList &L1,LinkList &L2,LinkNode *p[]){
if(L1->next=null||L2->next==null)
return false;
int a=maxValue(L1);
int b=maxValue(L2);
if(a>b)
List c[a];
else
List c[b];
answer(L1,c);
answer(L2,c);
int j=0;
for(int i=0;i<c.length;i++){
if(c[i]>1){
p[j]=c[i].p;
j++;
}
}
return true;
}
int maxValue(LinkList &L){
LNode *p=L->next;
int max=p->data;
while(p!=null){
if(p->data>max)
max=P->data;
p=p->next;
}
return max;
}
void answer(LinkList &L,List &c[]){
LNode *p=L->next;
int i;
while(p!=null){
i=P->data;
c[i].data=p->data;
c[i].p=p;
}
}

//删除偶数结点然后插到b队头
LinList saparate(LinkList &L1){
LNode *L2=(LNode *)malloc(sizeof(LNode));
L2->data=0;
L2->next=null;
//设L2是头节点
LNode *p=L->next;
LNode *pre=L;
int tempt;
int i=1
while(p!=null){
if(i%2==1){
p=p->next;
pre=pre->next;
}else{//尾插
pre->next=p->next;
if(L2->next==null){
L2->next=p->next;
p->next=null;
}else{
tempt=p->data;
p->data=L2->next->data;
L2->next->data=tempt;
P->next=L2->next;
L2->next=p;
}
p=pre->next;
i++;
}
}
retrue L2;
}

//同上一个的奇偶拆分,不多写
//同时要注意,这个插入方法还有要求,b1,bn是要求头插法

//因为是递增有序的,所以只要目前的等于下一个的数据,
//则删除下一个,遇到此类题最好还是画个图,然后用指针扫描着看
void delete(LinkList &L){
LNode *p=L->next->next;
LNode *q=L->next;
int i;
LNode *temot;
while(p!=null){
if(p->data==q->data){
tempt=p;
p=p->next;
q->next=p;
free(tempt);
}else{
p=p->next;
q=q->next;
}
}
}

//写的也许有点小问题,
//他原本是丹增的数列,要求单减,且在老头上
//所以比较万后应该继续头插
bool sort(LinkList &a,LinkList b){
if(a==null&&b==null){
return false;
}
LNode *p=a->next;
LNode *pre=q;
LNode *q=b->next;
LNode *preq=b;
while(p!=null&&q!=null){
if(q->data<p->data){
prep->next=q->next;
q->next=p;
pre->next=q;
q=prep->next;
pre=pre->next;
}else{
pre=pre->next;
p=p->next;
}
}
if(q==null){
return true;
}else{
p->next=q;
return true;
}
}

//思路于上面的找公共结点一样,只需要稍微修改一点。
//不多写
//思路2:两个指针移动。然后申请一个新链表,把值塞进去

bool find(LinkList &L,LinkList &B){
LNode *p=L->next;
LNode *q=B->next;
LNode *o;
while(p!=null){
while(q!=null){
q=B->next;
o=p;
if(q->data==p->data){
q=q->next;
o=o->next;
}else{
break;
}
}
if(q==null)
return true;
p=p->next;
}
return false;
}

bool answer(LinkList &L){
LNode *p=L->next;
LNode *q=L->pre;
if(p==null)
retrun false;
if(q==null)
return false;
int i=0;
while(p!=L){
i++;
p=p->next;
}
int c=0;
while(c<i/2){
if(p->data!=q->data){
return false;
}
p=p->next;
q=q->pre;
c++;
}
retrun true;
}
//这里用了计数器来计算遇到没遇到,但是还可以判断p->next==q
//or q=p;则对称。即相邻或相等

bool answer(LinkList &h1,LinkList &h2){
if(h1->next==null&&h2->next)
return false;
LNode *p=h2;
LNode *q;
if(p->next!=null){
while(p->next!=L){
p=p->next;
}
if(h1->next==null){
h1->next=h2->next;
p->next=h1;
h2->next=null;
return true;
}else{
p->next=h1->next;
h1->next=h2->next;
h2->next=null;
return true;
}
}else{
return true;
}

void answer(LinkList &L){
LNode *p=L->next;
LNode *pre=L;
LNode *temptpre=pre;
LNode *tempt=p;
int min=p->data;
while(p!=null){
if(p->data<min){
temptpre=pre;
tempt=p;
min=p->data;
}
p=p->next;
pre=pre->next;
}
LNode *u=tempt;
temptpre->next=tempt->next;
free(u);
}
void answer2(LinkList &L){
while(L!=null){
answer(L);
}
}

void answer(LinKList &L){
LNode *p=L->next;
int i=p->data;
while(p!=null){
if(p->data>i)
i=p->data;
p=p->next;
}//找最大值
int c[i];
int o=0;//长度
p=L->next;
while(P!=null){
c[p->data]++;
p=p->next;
o++;
}//统计频率
p=L->next;
while(p!=null){
p->frep=c[p->data];
p=p->next;
}//赋值
//比大小
while(c>0){
answer2(L);
o--;
}
}
void answer2(LinkList *L){
LNode *p=L->next->next;
LNode *pre=L->next;
LNode *tempt=p;
LNode *temptpre=pre;
int min=pre->freq;
while(p!=null){
if(p->freg<i){
i=p->freg;
tempt=p;
temptpre=pre;
}else{
p=p->next;
pre=pre->next;
}
}
temptpre->next=tempt->next;
tempt->next->pred=temptpre;
//删除
//插入
tempt-next=L->next;
L->next->pred=tempt;
tempt->pred=L;
L->next=tempt;
}

//算法思路,申明两个指针,探针法处理
int find(LinkList &L,int k){
if(L->next==null){
return 0;
}
LNode *p=L->next;
LNode *q=L->next;
int i=1;
while(P!=null&&i<k){
p=p->next;
i++;
}
if(i<k)
retrun 0;
while(p->next!=null){
q=q->next;
p=p->next;
}
printf(q->data);
return 1;
}

void delete(LinkList &L,int i){//写错了,写成了删除给定数值的结点
LNode *p=L->next;
LNode *pre=L;
int q=0;
int c;
while(p!=null){
c=answer2(p->data);
if(c==i){
if(q=0){
q++;
p=p->next;
pre=pre->next;
}else{
pre->next=p->next;
free(p);
p=pre->next;
}
}else{
p=p->next;
q=q->next;
}
}
}
int answer2(int a){
if(a>=0)
return a;
if(a<0)
return -a;
}
int answer2(int a){
if(a>=0)
return a;
if(a<0)
return -a;
}
void answer1(LinkList &L){
LNode *p=L->next;
LNode *pre=L;
int c[n];
int i;
while(p!=null){
i=answer2(p->data);
c[i]++;
if(c[i]>1){
pre->next=p->next;
free(p);
p=pre->next;
}else{
p=p->next;
pre=pre->next;
}
}
}

void answer(LinkList &L){
LNode *p=L->next;
LNode *q=L->next;
LNode *tempt;
LNode *temptpre;
LNode *o;
while(q->next!=null){
p=p->next;
q=q->next;
if(q->next!=null)
q-q->next;
}//找到中间结点
tempt=p->next->next;
temptpre=p->next;
while(tempt!=null){
o=tempt;
tempt=tempt->next;
//tempt移动
temptpre->next=o->next;
//删除
o->next=tempt;
p->next=o;
}//逆置
tempt=p->next;
temptpre=p;
o=L->next;
while(tempt!=null){
temptpre->next=tempt->next;
tempt->next=o->next;
o->next=tempt;
tempt=temptpre->next;
o=o->next->next;
}
}

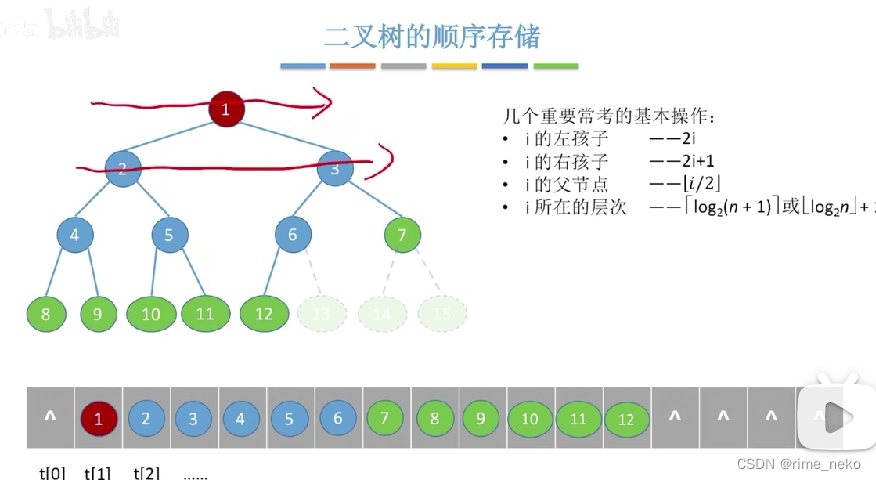
int answer(Tree T,int i,int j){
if(T[i]!=null&&T[j]!=null){
while(i!=j){
if(i>j)
i=i/2;
else
j=j/2;
}
return T[i];
}
}
先序中序和后序的一个模板
void a(Tree t){//先序
if(T!=null){
vist(t);
a(t->lchild);
a(t->rchild);
}
}

void notrecursion(BTree T){//中序
Initstact;
Btree p=T;
while(p!=null&&!IsEmpt(s)){
if(p!=null){
push(s,p);
p=p->lchilde;
}else{
pop(s,p);
visit(p);
p=p->rchild;
}
}
}//入栈向左一直走,出栈访问右子树
//后续
//入栈想租一直走,判定左子树,出栈访问,标记重置

int answer(BTree T){
if(T==null){
return 0;
}else{
int l=answer(T->lchild);
int r=answer(T->rchild);
if(l>r)
return l+1;
else
return r+1;
}
}

void answer(Btree T){
BNode *p;
if(T!=null){
t->lchild=p;
t->lChilde=t->rchild;
t->lchild-p;
answer(t->lchild);
answer(t->rchild);
}
}

int i=0;
void answer(Btree t){
int b[maxsize];
if(p!=null){
answer(t->lchild);
answer(t->rchild);
if(p->rchild!=null&&p->lchild!=null){
if(b[p->data]==0){
b[p->data]=1;
i++;
}
}
}
}

int answer(BTree t){
if(t!=null){
int i=answer(t->lchild);
int j=answer(t->rchild);
return j+1+i;
}else{
return 0;
}
}

int i;
int answer(Btree T,int k){
if(T!==null){
i++;
if(i==k){
return p->data;
}else{
answer(T->lchild,k);
answer(T->rchild,k);
}
}else{
return -1;
}
}

int answer(BTree t){
if(t!=null){
int i=answer(T->lchild);
int j=answer(T->rchild);
if(t->lchild==null&&t->rchild==null){
return i+1+j;
}else{
return i+j;
}
}else{
return 0;
}
}

void answer(BTree T,BNode &*p,int key){
if(T!=null){
if(T->data==key){
p=T;
}
answer(T->lchild,p,key);
answer(T->rchild.p.key);
}
}

BTNode *a=null;
void insert(BTree &T,BTree &head,BTree &tail){
if(T!=null){
insert(t->lchild,head,tail);
insert(t->rchild,head,tail);
if(T->lchild==null&&T->rchild==null)
if(a==null){
head=T;
tail=T;
}
else{
tail->rchild=T;
tail=T;
}
}
}
}

int find(BTree &T,BTNode *aim){
if(T!=null){
int a=find(T->lchild,aim);
int b=find(T->rchild,aim);
if(aim==T)
printf(a>b? a+1:b+1);
return a>b? a+1:b+1;
}else{
return 0;
}
}//这个代码还能更进,我写的没有考虑二叉排序树的性质。实际上不用递归也行

int find(BTree T,int deep){//设deep初值为1
if(T!=null){
int a=find(T->lchild,deep++);
int b=find(T->rchild,deep++);
if(T->lchild===null&&T->rchild==null){
retrun T->weight*deep+a+b;
}
}esle{
return 0;
}
}


void answer(BTree t,deep){
if(t==null){
return;
}esle if(t->lchild==null&&T->rchild==null)
printf("%s",t->data);
else{
if(deep>1)
printf("(");
answer(t->lchild,deep++);
printf("%s",t->data);
answer(t->rchild,deep++);
if(deep>1)
printf(")");
}
}
void main(){
answer(t,1);
}

int find(int i,Btree t,int deep){
if(t!=null){
if(t->data==i)
return deep;
else{
int a=find(i,t->lchild,deep++);
int b=find(i,t->rchild,deep++);
}
}else{
return 0;
}
}

void insert(Btree t,int deep){
if(T!=null){
if(deep==1)
t->parent=null;
if(deep>1)
if(t->lchild!=null)
t->lchild->parent=t;
if(t->rchild!=null);
t->rchild->parent=t;
BtNode l=t;
while(l!=null){
printf(l->data);
l=l->parent;
}
}
insert(t->lchild,deep++);
insert(t->rchild,deep++);
}
}

void answer(Btree t){
BTNode *p[maxsize];
int top=-1;
BTNode *q=t;
BTNode *r;
while(q!=null||top!=-1){
if(q!=null){
p[++top]=q;
q=q->lchild;
}
esle{
q=p[top];
if(q->right!=null&&q!=r){
q=q->right;
p[++top]=q;
q=q->lchild;
}else{
for(int i=0;i<top;i++){
printf(p[i].data);
}
q=p[top--];
r=q;
q=null;
}
}

动态顺序表查找
#define firstsize 10000;
typedef struct List{
int *data;
int maxsize;
int length;
}List;
void fiststep(List &a){
a.data=(int *)malloc(sizeof(int)*firstsize);
a.maxsize=firstsize;
a.length=0;
}
void add(List &a,int aim){
int *p=a.data;
a.data=(int *)malloc(sizeof(int)*(firstsize+aim));
for(int i=0;i<a.length;i++)
a[i]=p[i];
a.maxszie=firstsize+aim;
free(p);
}
直接插入
void insert(SList &L){
if(L==null)
return false;
int tempt;
int j;
for(i=i;i<l.length;i++){
if(l.data[i]<l.data[i-1])
tempt=a[i];
for(j=i-1;j>=0&&a[j]>a[i];j--){
a[j+1]=a[j];
}
a[j+1]=tempt;
}
}
}
二叉树遍历
void T(BTree t){
if(T!=null){
T(t->rchild);
T(t->lchild);
visit(t);
}
}
struct BtNode{
eleTyoe data;
struct BtNode *rchild;
sturct BtNode *lchild;
}*Btree,BNode;
希尔排序
int d,j,i
for(d=d/2;d>=1;d=d/2)
for(i=d+1;i<a.length;i++){
if(a[i]>a[i+1])
a[0]=a[i]
for(j=i-d;j>0&&a[j]>a[i];j=j-d)
a[j+d]=a[j]
a[j+d]=a[0]
}
双链表
typedef struct DLNode {
elemtype data
struct DLNode *next;
struct DLNode *prior;
}DLNode, *DLinkList;
void insert(DLinkList &l,int e,int data){//插入到第e个位置
DLNode *p=l->next;
DlNode *q=l;
int i=1;
DLNode *aim=(DLNode *)malloc(sizeof(DLNode));
aim->data=data;
aim->next=null;
aim->prior=null;
if(l==null)
return false;
if(e>0){
return false;
}
while(i!=e&&q!=null){
q=q->next;
p=p->next;
i++;
}
if(i==e&&q!=null){
if(p==null){
aim->next=null;
aim->prior=q;
q->next=aim;
}esle{
aim->next=p;
aim->prior=q;
q->next=aim;
p->prior=aim
}
return true;
}esle{
return false;
}
}
队列
规定元素输入和输出方向的数据结构,即先进先出。
队头等于队尾,则是空队列
直接插入
void insert(int a[]){
int tempt,j;
for(int i=i;i<a.length;i++){
if(a[i]>a[i-1]){
tempt=a[i];
for(j=i;j>0&&a[j]<a[i];j--)
a[j+1]=a[j];
a[j+1]=tempt;
}
}
}
void insert(LinkList &L,int x){
LNode *p=(LNode *)malloc(szieof(LNode));
p->data=x;
p->next=null;
if(L==null)
return false;
LNode *q=L->next;
LNode *a=L->next;
while(q!=null){
if(q->data>p->data){
q=q->next;
a=a->next;
}else{
break;
}
}
p->next=q;
a->next=p;
}
void ceng(BTree t){
if(t!=null){
LinkQ q;
int i=0;
firststep(q);
Btree a=t;
enLink(q,a);
while(!isEletype(q)){
outLink(q,a);
i++;
if(a->lchild!=null)
enLink(q,a->lchild);
if(a->rchild!=null)
enLink(q,a->rchild);
}
}
冒泡排序
void swap(int a,int b){
int tempt=a;
a=b;
b=tempt;
}
void pop(int a[]){
bool q=true;
for(int i=0;i<sizeof(a);i++){
q=true;
for(j=a.length-1;j>=i;j--){
if(a[j]<a[j-1]){
swap(a[j],a[j-1]);
q=false;
}
}
if(q){
break;
}
}
}
sturct Lnode{
int data;
int next;
}
lnode a[1000]





















 314
314

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










