区间系统鲁棒PID设计

区间系统鲁棒PID控制器设计

I. 引言

工业中最广泛使用的控制器是PI（比例‐积分）、PID （比例‐积分‐微分）以及超前/滞后控制器。目前，针对这些控制器的整定开展了大量的研究工作。许多研究人员已经研究了能够稳定整个被控对象的P、PI和PID控制器集合，如Ho等人[1‐3]所建议的那样。在[1]中提供了一种利用基于解析解的方法的埃尔米特‐比勒定理。一种基于线性规划的技术用于求取可稳定给定被控对象的控制器参数，该方法见于[2]。该方法计算效率高，并揭示了不同类型控制器的重要特性。他们证明了稳定控制器增益的集合位于一个凸集内。一种基于奈奎斯特图的更快速方法见于[4,5]。基于稳定边界轨迹和参数空间法的PI和PID控制器设计分别见于[6]和[7]。

超前/滞后补偿器是利用给定被控对象的固定参数设计的。然而，大多数实际过程参数并不能精确获知，这意味着系统存在不确定性。近年来，Kharitonov的结果被广泛应用于相关研究中，在参数不确定性条件下的鲁棒控制器设计领域也取得了许多进展。针对以区间对象形式表示的不确定控制系统，已对其稳定性和性能进行了分析[8]。

比普拉布等人[9]提出了一种利用基于粒子群优化的自动定量反馈理论设计一阶加纯滞后过程模型PID控制器的方法。拉德克等人[10]提出了一种通过将特征方程的实部和虚部分别相等并求解稳定区域来确定控制器参数的方法。在[11]中采用了一种优化且自动化的方法，该方法使用定量反馈理论满足所有鲁棒设计规范。王元杰[12]针对开环不稳定对象，通过图形化方法计算了满足全部可行增益裕度和相位裕度规范的鲁棒PID控制器。

II. 赫里通诺夫定理

该定理通过使用四个具有实系数的顶点多项式来分析区间系统的稳定性特性。这些多项式的系数具有上下限。通过将劳斯判据应用于这四个称为赫里通诺夫多项式的多项式，可以确定该集合的稳定性。

对于形如
$$ \delta(s) = \delta_0 + \delta_1 s + \delta_2 s^2 + \delta_3 s^3 + \cdots + \delta_n s^n $$
的多项式，其中系数位于给定范围内，
$$ \delta_0 \in [a_0, b_0],\ \delta_1 \in [a_1, b_1],\ \ldots,\ \delta_n \in [a_n, b_n] $$

定义四个Kharitonov多项式：
$$
\begin{aligned}
K_1(s) &= a_0 + a_1 s + b_2 s^2 + b_3 s^3 + a_4 s^4 + \cdots \
K_2(s) &= a_0 + b_1 s + b_2 s^2 + a_3 s^3 + a_4 s^4 + \cdots \
K_3(s) &= b_0 + a_1 s + a_2 s^2 + b_3 s^3 + b_4 s^4 + \cdots \
K_4(s) &= b_0 + b_1 s + a_2 s^2 + a_3 s^3 + b_4 s^4 + \cdots
\end{aligned}
\tag{1}
$$

III. 求取所有稳定化控制器参数的集合

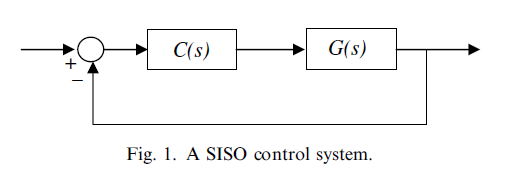
考虑一个由 $ G(s) $ 给出的单输入单输出被控对象及其对应的由 $ C(s) $ 给出的PID控制器，如下所示，
$$ G(s) = \frac{N(s)}{D(s)} \tag{2} $$

本文所考虑的PID控制器结构如下，
$$ C(s) = K_p + \frac{K_i}{s} + K_d s \tag{3} $$

为了获得控制器参数的极限值，我们首先需要确定最小增益裕度和相位裕度指标。可以固定其中一个参数，以得到包含另外两个参数的图形。在本研究中，固定了 $ K_d $，并求出了 $ K_p $ 和 $ K_i $ 的范围。

考虑二阶被控对象，
$$ G(s) = \frac{K}{(T_1 s - 1)(T_2 s - 1)} e^{-Ls} \tag{4} $$

以下是所考虑的上下界，
$$
\begin{aligned}
T_z &= [4.5, 5.5],\quad L = [0.9, 1.1],\quad T_1 = [9, 11],\
T_2 &= [4.5, 5.5],\quad K = [0.9, 1.1]
\end{aligned}
$$

设计要求是：
- 最小相位裕度 $ PM = 21^\circ $
- 最小增益裕度 $ GM = 2 $

$ K_d $ 值从[13]中选取为 $ K_d = 5 $。然后通过在 $ G(j\omega) $ 中代入不同的 $ \omega $ 值得到轨迹。为了利用稳定边界轨迹绘制 $ K_p $ 与 $ K_i $ 之间的关系图，并固定 $ K_d $，根据[14]中给出的方法需要确定 $ N_e(-\omega^2) $、$ N_o(-\omega^2) $、$ D_e(-\omega^2) $ 和 $ D_o(-\omega^2) $。为了简化计算以便在MATLAB中使用，我们采用以下推导出的关于增益裕度和相位裕度的公式[16]：

对于稳定性和增益裕度，必须考虑以下方程：
$$
K_p = \frac{\sin \varphi}{GM \cdot |G(j\omega)|},\quad
K_i = K_d \omega^2 + \frac{K_p \tan \varphi}{\omega}
\tag{5}
$$
其中 $ \varphi = -90^\circ - \arg(G(s)) $

对于相位裕度，
$$
K_p = \frac{\cos \theta}{|G(j\omega)|},\quad
K_i = K_d \omega^2 - \frac{\sin \theta}{|G(j\omega)| \cdot \omega}
\tag{6}
$$
其中 $ \theta $ 为期望的相位裕度，$ \omega $ 为未补偿系统的相位裕度。

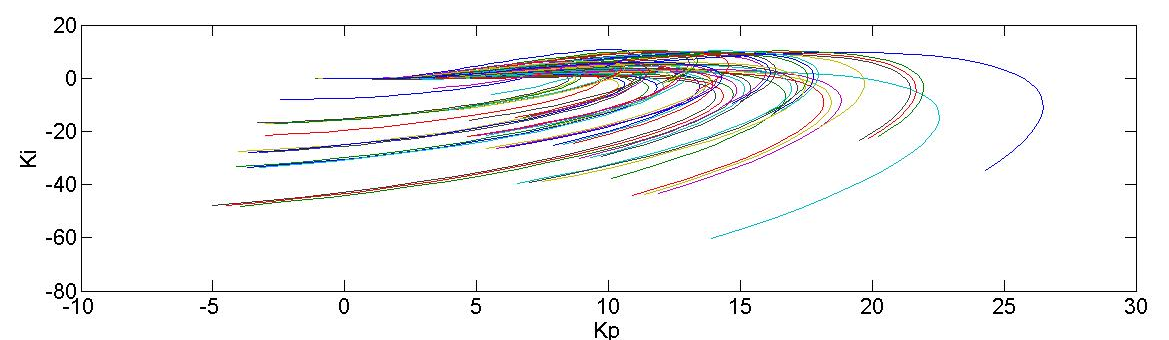
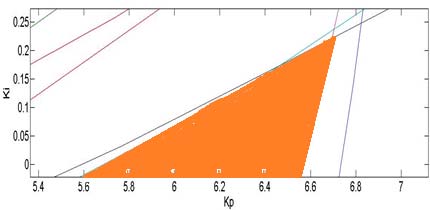
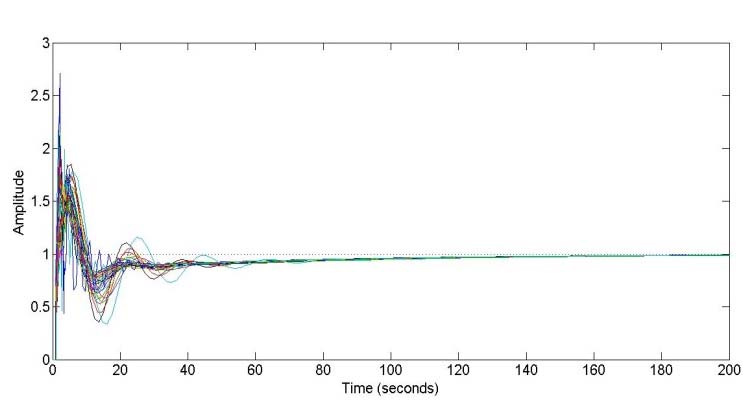
考虑了与系统所有参数相关的参数不确定性。因此，可以通过绘制所有32种组合的不确定性（$ 2^n $）来验证稳定性。通过将增益裕度保持为 $ GM = 1 $，得到稳定性曲线。其余曲线是针对指定的裕度值（GM和PM）获得的。图2给出了在给定过程具有固定 $ K_d $ 的情况下，具有共同稳定性、GM和PM的曲线。这些曲线所得到的公共区域在图3中进行了放大。伺服和调节响应分别在图4中给出，对应于 $ K_d = 5 $、$ K_p = 6.5 $、$ K_i = 0.13 $。

IV. 鲁棒控制器设计

基于标称系统参数设计的控制器在存在参数变化时可能无法稳定整个闭环系统。然而，我们要求最终的控制器必须尽可能接近标称控制器，同时保持闭环稳定性[17]。设 $ \theta $ 为所有使特征多项式的零点位于s平面左半部分的控制器参数向量构成的集合。控制器设计的目标是从标称控制器参数 $ k_0 $ 出发，在容许集 $ \theta $ 中搜索一个控制器参数向量。鲁棒控制器设计可表述为，
$$ J = \min_{k \in \theta} | k - k_0 |^2 \tag{7} $$

以下是为区间对象寻找鲁棒PID控制器参数的步骤：
1. 选择合适的极点配置方法。所得控制器参数为 $ K_{p0} $、$ K_{i0} $ 和 $ K_{d0} $。
2. 使用以下给出的目标函数进行优化，约束条件由定理1和定理2确定。
$$
J = (K_p - K_{p0})^2 + (K_i - K_{i0})^2 \quad \text{(or)}
$$
$$
J = (K_p - K_{p0})^2 + (K_i - K_{i0})^2 + (K_d - K_{d0})^2
\tag{8}
$$

使用稳定性赫尔维茨判据来建立约束条件。定理1和2给出了区间多项式稳定性的充分必要条件[15]。考虑一个较小的 $ \in $，这会得到不同的控制器参数值。当 $ \in $ 增加时，调节时间减少，但当我们进一步增加其值[17]时，系统将变得不稳定。考虑形如的n次实系数多项式集合，
$$ \delta(s) = \delta_0 + \delta_1 s + \delta_2 s^2 + \delta_3 s^3 + \cdots + \delta_n s^n \tag{9} $$
其中系数位于给定范围 $ \delta_0 \in [x_0, y_0] $，$ \delta_1 \in [x_1, y_1] $，…，$ \delta_n \in [x_n, y_n] $ 内。

定理1 ：对于所有 $ \delta_i \in [x_i, y_i] $，其中 $ i = 0, 1, 2, \ldots, n $，若满足以下必要条件，则所定义的区间多项式 $ \delta(s) $ 是Hurwitz的：
$$
\begin{aligned}
y_i &\ge x_i > 0, \quad i = 0, 1, 2, \ldots, n \
x_i x_{i+1} &> y_{i-1} y_{i+2}, \quad i = 1, 2, \ldots, n – 2
\end{aligned}
\tag{10}
$$

定理2 ：如果满足以下充分条件，则对所有 $ \delta_i \in [x_i, y_i] $（其中 $ i = 0, 1, 2, \ldots, n $）定义的区间多项式 $ \delta(s) $ 是赫尔维茨的：
$$
\begin{aligned}
y_i &\ge x_i > 0, \quad i = 0, 1, 2, \ldots, n \
0.4655 x_i x_{i+1} &> y_{i-1} y_{i+2}, \quad i = 1, 2, \ldots, n – 2
\end{aligned}
\tag{11}
$$

A. 稳定一阶加纯滞后系统的控制器设计

考虑具有给定不确定性的稳定一阶时滞过程的以下模型，
$$ G(s) = \frac{K e^{-Ls}}{Ts + 1} \tag{12} $$
其中 $ T = [0.9, 1.1] $，$ K = [0.8, 1.2] $，$ L = [0.29, 0.31] $。

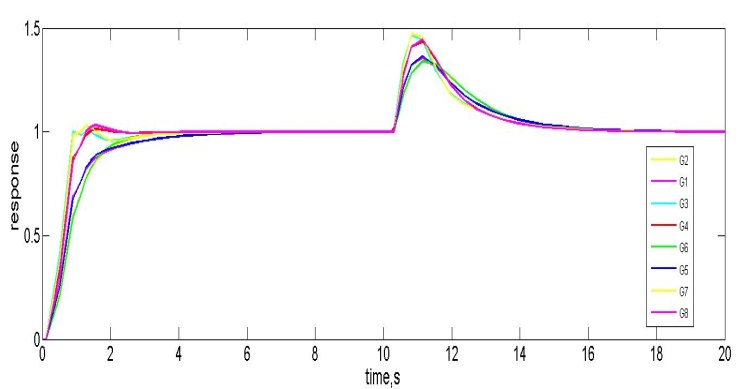
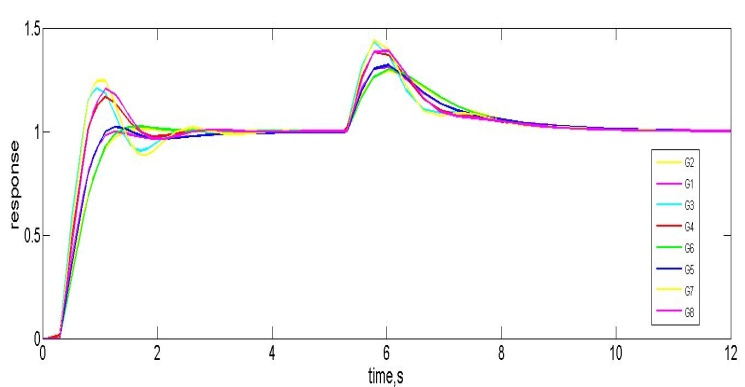
文献中提供了多种针对一阶加纯滞后过程的鲁棒控制技术。本文采用IMC调参，因为它是应用最广泛的技术之一。实施了由[18]提出的设定。其中，$ \lambda $ 为鲁棒性参数，其取值应为 $ \lambda > 1.7L $。当 $ \lambda = 0.8 $ 时，得到 $ K_{p0} = 1.4375 $ 和 $ K_{i0} = 1.25 $ 的值。图6给出了扰动被控对象的伺服和调节响应。在构建约束条件时，时滞近似处理如下：
$$ e^{-Ls} = \frac{1}{1 + Ls} \tag{13} $$

目标函数在满足以下约束条件的情况下被最小化：
$$
\begin{aligned}
-0.952 K_p + 0.4092 K_i - 1.19 + \in &\le 0 \
-0.952 K_p + 0.8790 K_i - 1.19 + \in &\le 0 \
-1 - 0.8 K_p + \in &\le 0 \
-1 - 1.2 K_p + \in &\le 0 \
-0.8 K_i + \in &\le 0 \
-1.2 K_i + \in &\le 0
\end{aligned}
\tag{14}
$$

优化之后，控制器设定为 $ K_p = 2.0569 $ 和 $ K_i = 1.875 $（对应 $ \in = 1.5 $）。表1比较了优化前后控制器设定的性能。

模型	方法	Kp	Ki	ITAE (Ser+Reg)
标称系统，G	IMC	1.4375	1.25	6.62
标称系统，G	之后 优化	2.0569	1.875	3.95
G1 K=0.8, T=0.9, L=0.29	IMC	1.4375	1.25	6.014
G1 K=0.8, T=0.9, L=0.29	之后 优化	2.0569	1.875	3.941
G2 K=0.8, T=1.1, L=0.29	IMC	1.4375	1.25	6.427
G2 K=0.8, T=1.1, L=0.29	之后 优化	2.0569	1.875	3.887
G3 K=1.2, T=0.9, L=0.29	IMC	1.4375	1.25	5.95
G3 K=1.2, T=0.9, L=0.29	之后 优化	2.0569	1.875	3.883
G4 K=1.2, T=1.1, L=0.29	IMC	1.4375	1.25	6.755
G4 K=1.2, T=1.1, L=0.29	之后 优化	2.0569	1.875	3.779
G5 K=0.8, T=0.9, L=0.31	IMC	1.4375	1.25	6.57
G5 K=0.8, T=0.9, L=0.31	之后 优化	2.0569	1.875	3.949
G6 K=0.8, T=1.1, L=0.31	IMC	1.4375	1.25	6.59
G6 K=0.8, T=1.1, L=0.31	之后 优化	2.0599	1.875	3.904
G7 K=1.2, T=0.9, L=0.31	IMC	1.4375	1.25	6.5
G7 K=1.2, T=0.9, L=0.31	之后 优化	2.0569	1.875	3.902
G8 K=1.2, T=1.1, L=0.31	IMC	1.4375	1.25	6.23
G8 K=1.2, T=1.1, L=0.31	之后 优化	2.0569	1.875	3.833
## B. 不稳定FOPTD的控制器设计

考虑一个不稳定的带延迟的一阶过程，
$$ G(s) = \frac{K e^{-Ls}}{Ts - 1} \tag{15} $$
其中 $ T = [3.8, 4.2] $，$ K = [3.8, 4.2] $，$ L = [1.9, 2.1] $。

延迟项近似如下，
$$ e^{-Ls} = \frac{1 - 0.5Ls}{1 + 0.5Ls} \tag{16} $$

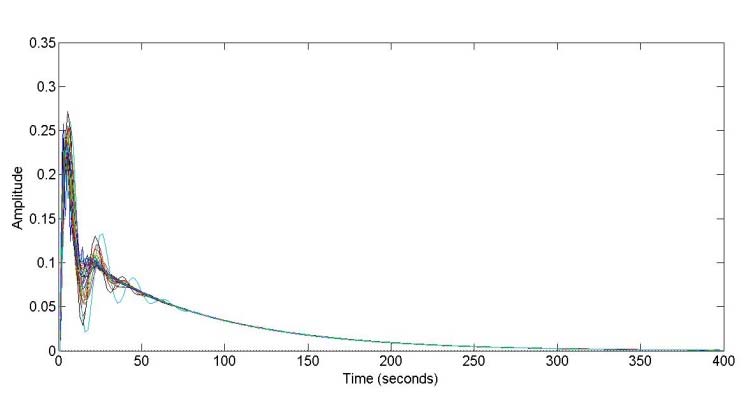
文献[19]中提出的极点配置方法给出了 $ K_p = 0.35 $、$ K_i = 0.0154 $、$ K_d = 0.4777 $。图8给出了该控制器设定下所有扰动被控对象的响应。所施加的约束条件如下，其中 $ \in = 0 $：
$$
\begin{aligned}
-3.8 K_i + \in &\le 0 \
-4.2 K_i + \in &\le 0 \
3.61 K_p - 4.2 K_d - 3.15 + \in &\le 0 \
4.41 K_p - 3.8 K_d - 2.85 + \in &\le 0 \
16.7 K_p^2 - 15.2 K_p + 30.6 K_i + 3.8 K_d - 19.4 K_p K_i + 1.6 K_i K_d - 14.4 K_p K_d + 2.8 + \in &\le 0 \
16.7 K_p^2 - 15.2 K_p + 51.4 K_i + 3.8 K_d - 19.4 K_p K_i - 15.8 K_i K_d - 14.4 K_p K_d + 2.8 + \in &\le 0 \
4.41 K_d - 3.705 + \in &\le 0 \
3.61 K_d - 4.305 + \in &\le 0
\end{aligned}
\tag{17}
$$

优化之后，$ K_p = 0.5618 $、$ K_i = 0.0921 $ 和 $ K_d = 0.6472 $。表2比较了不稳定的FOPTD过程的ITAE性能。

模型	方法	Kp	Ki	Kd	ITAE (Ser+Reg)
Nom. 被控对象，G	Pole 配置	0.35	0.015	0.48	36630
Nom. 被控对象，G	之后 优化	0.56	0.092	0.65	4938
G1 K=3.8, T=3.9, L=1.9	Pole 配置	0.35	0.015	0.48	37070
G1 K=3.8, T=3.9, L=1.9	之后 优化	0.56	0.092	0.65	5269
G2 K=3.8, T=2.1, L=1.9	Pole 配置	0.35	0.015	0.48	39800
G2 K=3.8, T=2.1, L=1.9	之后 优化	0.56	0.092	0.65	5466
G3 K=4.1, T=3.9, L=1.9	Pole 配置	0.35	0.015	0.48	40520
G3 K=4.1, T=3.9, L=1.9	之后 优化	0.56	0.092	0.65	5962
G4 K=4.1, T=2.1, L=1.9	Pole 配置	0.35	0.015	0.48	40440
G4 K=4.1, T=2.1, L=1.9	之后 优化	0.56	0.092	0.65	3989
G5 K=3.8, T=3.9, L=2.1	Pole 配置	0.35	0.015	0.48	24200
G5 K=3.8, T=3.9, L=2.1	之后 优化	0.56	0.092	0.65	5956
G6 K=3.8, T=4.1, L=2.1	Pole 配置	0.35	0.015	0.48	23910
G6 K=3.8, T=4.1, L=2.1	之后 优化	0.56	0.092	0.65	4172
G7 K=4.2, T=3.9, L=2.1	Pole 配置	0.35	0.015	0.48	25940
G7 K=4.2, T=3.9, L=2.1	之后 优化	0.56	0.092	0.65	4325
G8 K=4.2, T=4.1, L=2.1	Pole 配置	0.35	0.015	0.48	2590
G8 K=4.2, T=4.1, L=2.1	之后 优化	0.56	0.092	0.65	4402

C. 控制器设计 for unstable CSTR

由[20]提出的等温CSTR的数学模型方程为，
$$ \frac{dc}{dt} = \frac{Q}{V}(c_f - c) - \left[ \frac{k_1 c}{(k_2 c + 1)^2} \right] \tag{18} $$
其中 $ Q $ 和 $ c_f $ 分别为入口流量和进料浓度。选定的 $ Q $ 和 $ V $ 分别为 $ Q = 0.03333 \, \text{l/s} $，$ V = 1 \, \text{l} $。

通过修改 $ k_1 $ 和 $ k_2 $ 的值以获得不同的操作区域。本文考虑了三个操作区域。对于每个操作区域，模型方程的稳态解给出三个解，其中中间值为不稳定稳态，其余两个为稳定稳态。当在不稳定稳态附近对CSTR方程进行线性化时，得到一个一阶不稳定传递函数。选择不同的 $ k_1 $ 和 $ k_2 $，并对应相应的不稳定状态，过程参数如表3所示。

考虑测量时延 $ L = 8.5 $，且无不确定性。因此，过程参数的变化范围现在为
$$ K = [0.416, 0.744],\quad \tau = [12.48, 22.29],\quad L = [8.5, 8.5] $$
延迟项按公式(16)进行近似。

将平均模型视为标称系统，并设计控制器。利用[19]中提出的极点配置技术，确定了平均模型的控制器设定。得到的参数值为 $ K_{p0} = 4.8 $、$ K_{i0} = 0.035 $ 和 $ K_{d0} = 19.20 $。随后在以下约束条件下对目标函数进行最小化，
$$
\begin{aligned}
-0.416 K_i + \in &\le 0 \
-0.744 K_i + \in &\le 0 \
-0.17 K_p K_d - 1.65 K_p + 78.83 K_i + 0.416 K_d + 3.98 + \in &\le 0 \
-0.17 K_p K_d - 1.65 K_p + 169.35 K_i + 0.416 K_d + 3.98 + \in &\le 0 \
-0.744 K_p + 1 + \in &\le 0 \
-0.416 K_d - 13.8 + \in &\le 0 \
-0.744 K_d - 13.8 + \in &\le 0 \
-0.416 K_p + 1 + \in &\le 0
\end{aligned}
\tag{19}
$$

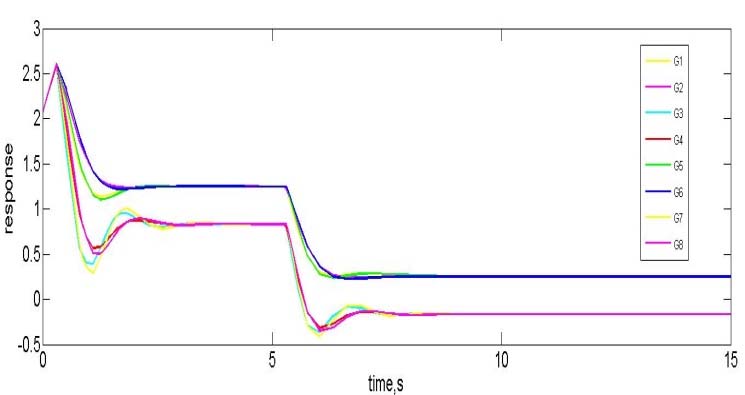
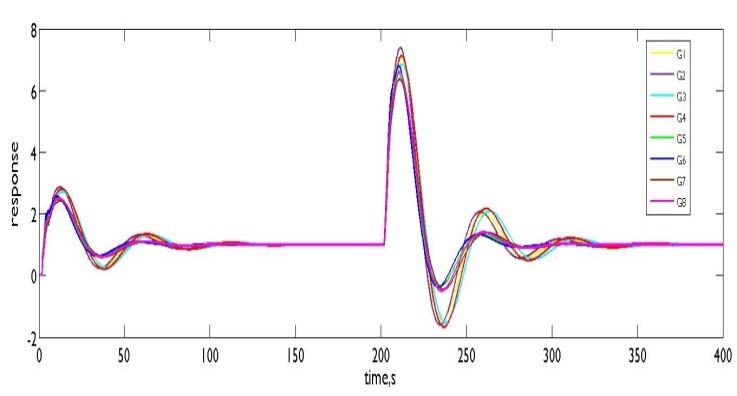
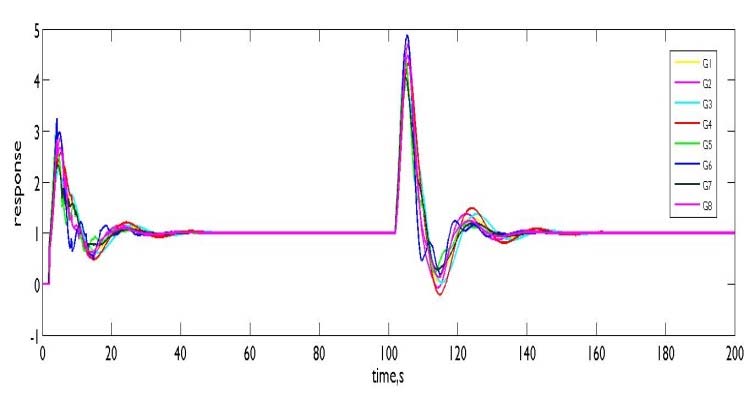
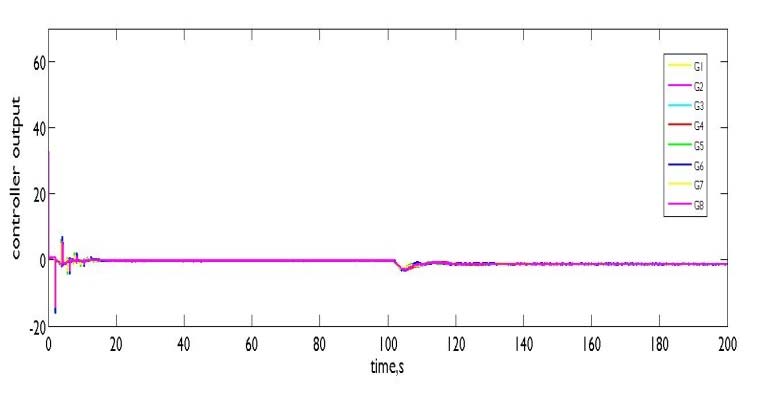
优化后的控制器设定为 $ K_p = 5.109 $、$ K_i = 0.0601 $ 和 $ K_d = 19.221 $，对应 $ \in = 0.05 $。图11、12和13显示了在不同初始条件（$ c = 0.8527 $、$ 0.5965 $ 和 $ 0.715 $）下但相同设定值（$ SP = 0.7 $）的响应。伺服‐调节响应的闭环性能在表4中进行了比较。

模型	K1	K2	c	K	τ
G1	12	12	0.8527	0.744	22.29
G2	11	12	0.715	0.542	16.26
G3	10	12	0.5965	0.416	12.48

模型	方法	Kp	Ki	Kd	ITAE (Ser+Reg)
G1	Pole 配置	2.468	0.025	14.31	13000
G1	之后 优化	3.437	0.120	14.98	3466
G2	Pole 配置	2.468	0.025	14.31	18750
G2	之后 优化	3.437	0.120	14.98	5489
G3	Pole 配置	2.468	0.025	14.31	23060
G3	之后 优化	3.437	0.120	14.98	7097

V. 结论

本文采用一种基于计算PID控制器参数极限值的方法，用于确定具有两个不稳定极点和时滞的二阶过程的控制器设定。该方法无需进行任何复杂计算或使用线性规划技术来求取参数，因此可通过这一简单方法获得一组满足所需稳定性指标的控制器。此外，还提出了一种两步法，用于为多种过程设计鲁棒控制器，并将其性能与标称系统的控制器设定进行了比较。结果表明，鲁棒控制器不仅提高了稳定性，还改善了区间对象的性能。