小议神经网络训练与Sigmoid 函数

1. 神经网络训练过程

我们分析一下下面这个简单的模型：

$$\begin{gathered} y=w_1{x}_1+w_2{x}_2+w_0 \\ z=\beta (y)\text{\hspace{1em}(1)} \end{gathered}$$

需要依据训练样本，确定参数 $w_1,w_2,w_0$ 的值。如何确定使模型与训练样本尽量匹配？一般借助损失函数来解决这个问题。

2. 损失函数

最简单的想法是，用模型预测训练样本，用预测错误的次数作为损失函数的结果：

$$Loss(w_1,w_2,w_0)=模型预测错误的个数\text{\hspace{1em}(2)}$$

接下来，只需要让 $w_1,w_2,w_0$ 朝着损失函数降低的方向变化就行了。如上图，分界线逐步移动到$Loss(w_1,w_2,w_0)=0$ 的位置。

说起来容易，实际做起来问题还不少。参考下图：

神经网络模型在训练的时候，是根据Loss函数的变化来判断变化的方向是否正确。上图中，虽然参数发生了变化，但是 $Loss(w_1,w_2,w_0)=0$ 却没发生变化。导致这个结果的原因是激活函数 $\beta (\ast )$ 的定义，$\beta (0.01)$ 和 $\beta (10000)$ 的值完全相同，因此，它无法区分 0.01 和 10000 谁离分界线更远一些、谁离分界线更近一些。这导致分界线在小幅度变化过程中，激活函数 $\beta (\ast )$ 无法给出提示。就像学生考试一样，第一次考了61分，改变学习方法后，第二次考了75分。如果这两个成绩反映在成绩单上都是“及格”，因此，我们就不知道新的学习方法是否有效。因此，我们需要一种更好的激活函数，以便反映出模型细微进步或退步，使得参数能朝着正确方向逐步调整。

3. Sigmoid 函数

下面就是著名的 Sigmoid 函数，当自变量 x 很小的时候，它的值接近0，当 x 逐渐增大的时候，它的值逐渐接近1。因为它是个严格递增函数，因此，无论 x 在那个区间内变化，Sigmoid 函数都能随之展现出变化。

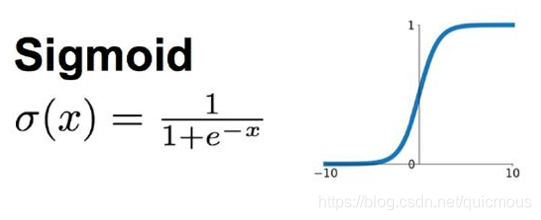
把激活函数更换成 Sigmoid 函数，模型 (1) 变成如下形式：

$$z=\sigma (w_1{x}_1+w_2{x}_2+w_0)\text{\hspace{1em}(3)}$$

假设训练样本为 $(x_{1i},x_{2i},z_i),i=1,2,...,N$，可以简单地按照如下方式定义损失函数：
$$Loss(w_1,w_2,w_0)=\sum _{i=1}^N|(w_1{x}_{1i}+w_2{x}_{2i}+w_0)-z_i|\text{\hspace{1em}(4)}$$

当然，简单的未必好用，回头我们将进一步讨论如何科学地设计损失函数。