Python对撞指针（力扣）

喜欢那双眼动人.

已于 2023-11-04 18:15:03 修改

阅读量893

点赞数 23

CC 4.0 BY-SA版权

分类专栏：力扣文章标签： leetcode 算法

于 2023-11-04 18:13:26 首次发布

本文链接：https://blog.youkuaiyun.com/qq_64334741/article/details/134220383

力扣专栏收录该内容

8 篇文章

订阅专栏

文章介绍了指针的三种类型及其在算法中的应用，如对撞指针用于有序数组的查找问题，快慢指针处理数组操作，分离双指针解决集合运算。以两数之和和三数之和为例，展示了如何利用指针优化暴力枚举的方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一.概念

指针通常分为三类:(本文主要讲述对撞指针)

对撞指针：两个指针方向相反。适合解决查找有序数组中满足某些约束条件的一组元素问题、字符串反转问题。

快慢指针：两个指针方向相同。适合解决数组中的移动、删除元素问题，或者链表中的判断是否有环、长度问题。

分离双指针：两个指针分别属于不同的数组 / 链表。适合解决有序数组合并，求交集、并集问题。

通常做算法题时，最容易想到的就是暴力枚举。个人觉得双向指针是属于枚举中的优化选项。暴力枚举在oj上通常容易超时。

二.例题讲解（两数之和）

https://leetcode.cn/problems/two-sum-ii-input-array-is-sorted/description/（167. 两数之和 II - 输入有序数组）

题目描述:

给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

示例 1：

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

方法一：

看到题目时，首先就想到了暴力枚举。两层for循环就能搞定

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
         for i in range(len(numbers)):
            for j in range(i+1,len(numbers)):
                if numbers[i]+numbers[j]==target:
                    return [i+1,j+1]

# 时间复杂度O(n^2)
# 空间复杂度O(1)

这个代码可以通过绝oj的绝大部分测试用例。对于比赛时没有思路和时间不够的情况下是适用的。

方法二:

1.重新审题:

1.下标从 1 开始的整数数组 numbers(注意Python数组下标是从0开始的)

2.数组已按 非递减顺序排列(数组是有序的)

3.数组中找出满足相加之和等于目标数 target 的两个数

4.以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2

2.思路:

因为数组已按 非递减顺序排列(数组是有序的)，假设numbers = [2,4,5,7,11,14,15,21], target = 9

定义left为左指针；right为右指针

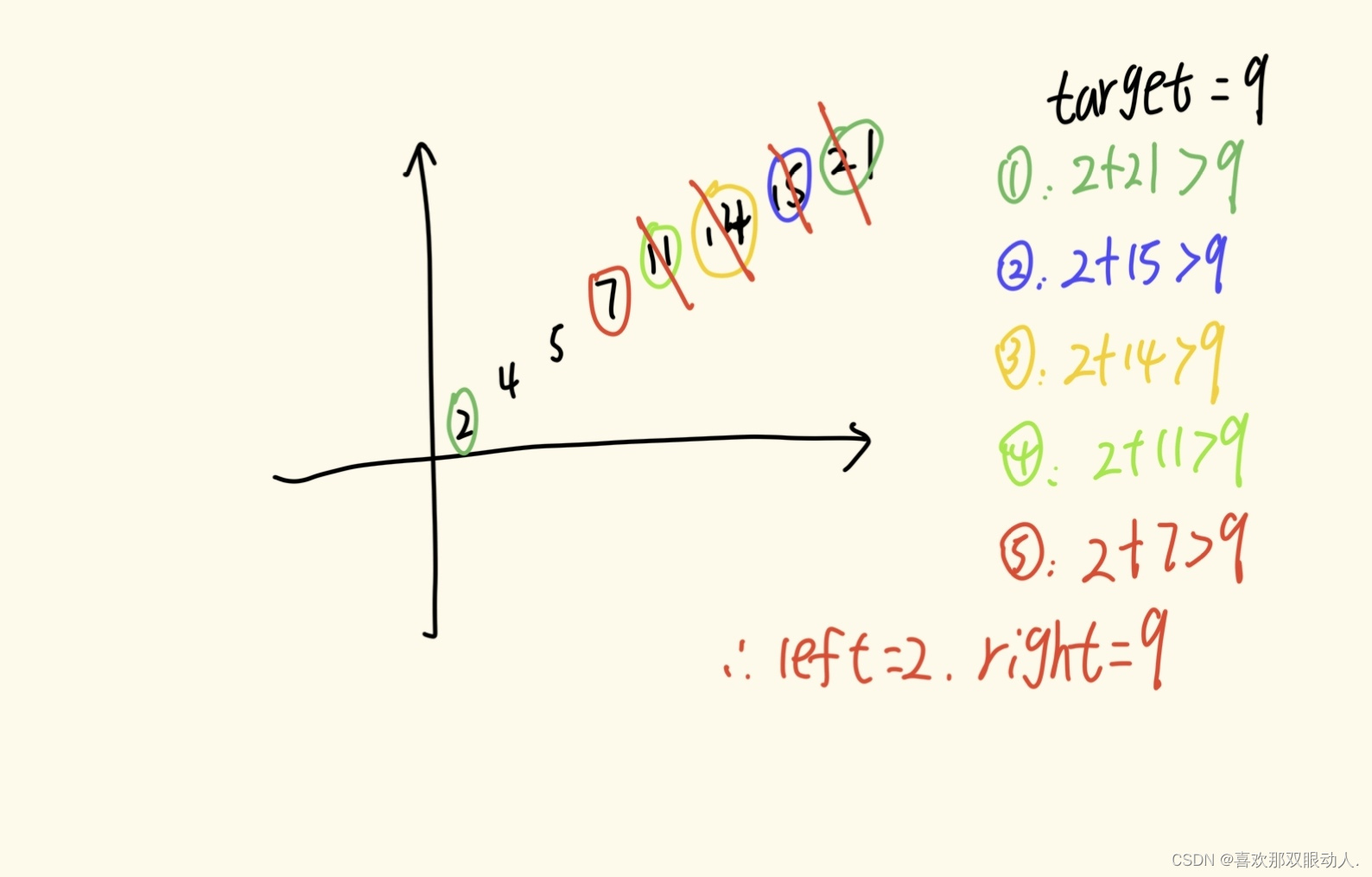
代码实现(Python)

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        left=0 # 定义左指针（指向第一个数）
        right=len(numbers)-1  # 定义右指针（指向最后一个数）
        while left<right:  # 一直循环直到找到符合条件的
            if numbers[left]+numbers[right]==target:
                return [left+1,right+1]
            elif numbers[left]+numbers[right]<target:
                left=left+1
            else:
                right=right-1


# 时间复杂度O(n)
# 空间复杂度O(1)

三.升级版(三数之和)

https://leetcode.cn/problems/3sum/description/(15.三数之和)

题目描述:

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

刚开始看到题的时候，有点没读懂

1.重新读题:

1.判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k

2.nums[i] + nums[j] + nums[k] == 0

3.返回所有和为 0 且不重复的三元组

4.答案中不可以包含重复的三元组([-1,0,1]与[1,0,-1是相同的])

5.输出的顺序和三元组的顺序并不重要([[-1,-1,2],[-1,0,1]]与[[-1,0,1],[-1,-1,2]]是相同的){其实挺好奇oj是怎么评判的}

三数之和和两数之和的区别在哪里呢？

1.两数之和只有一个返回值，三数之和允许有多个返回值

2.两数之和给定的数组是有序的，而三数之和给定的数组是无序

思路:

nums[i] + nums[j] + nums[k] == 0 ---> nums[j] + nums[k] == -nums[i]

首先将i确定为第一个数,然后就变成了两数之和的版本

值得注意的点:

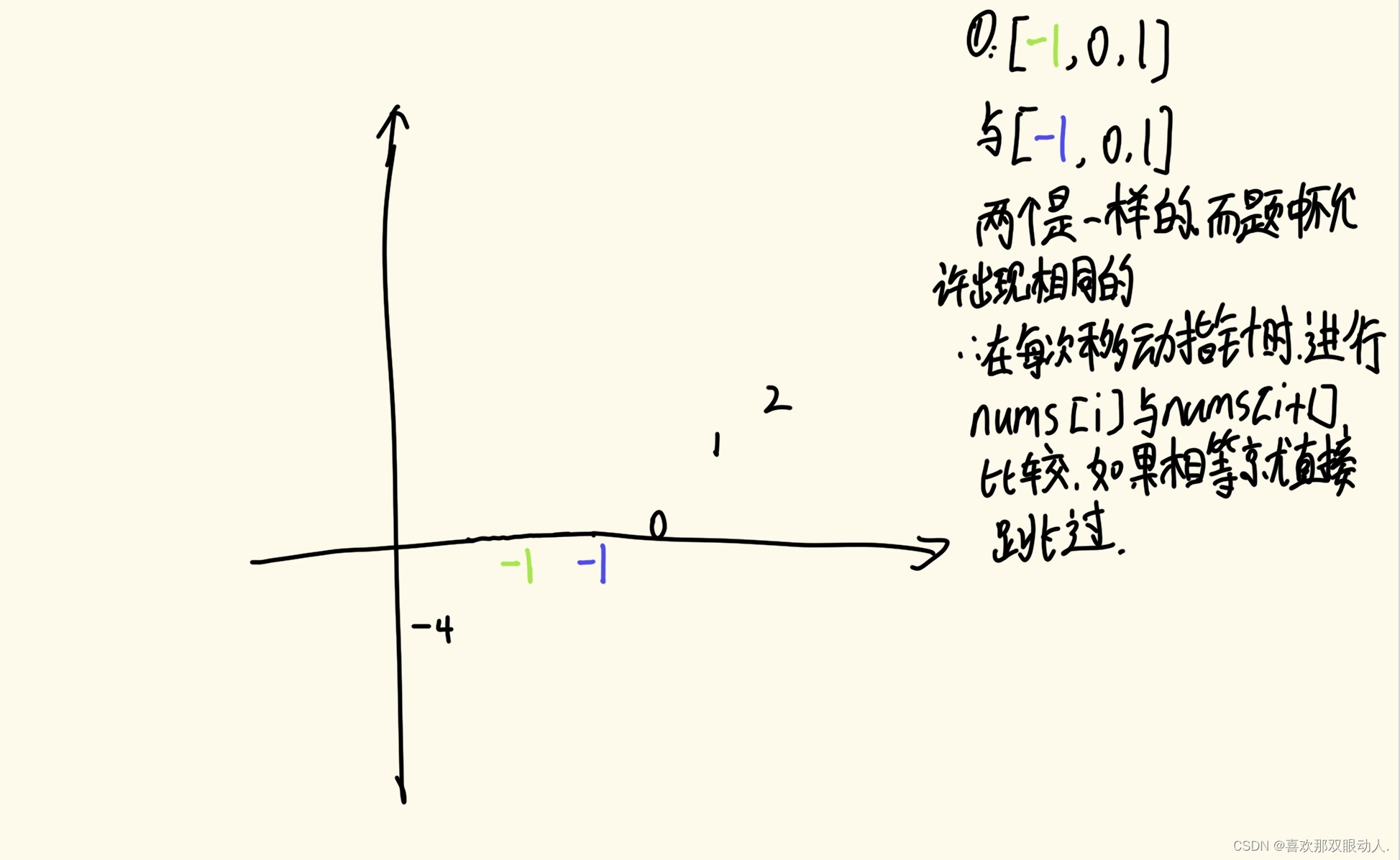
class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        nums.sort() # 使用指针前先对数组进行排序
        ans=[]
        for i in range(len(nums)-2): # 因为是三个数，而target为最小的。要留两个数在后面
            target=nums[i]
            if i>0 and target==nums[i-1]: # 防止出现[-1,0,1][-1,0,1] 跳过重复i
                continue
            left=i+1 # 定义左指针
            right=len(nums)-1 # 定义右指针
            while left<right: # 两数之和模板
                if nums[left]+nums[right]+target<0:
                    left=left+1
                elif nums[left]+nums[right]+target>0:
                    right=right-1
                else:
                    ans.append([nums[left], nums[right], target])
                    left+=1 
                    while left<right and nums[left]==nums[left-1]:
                        left+=1  # 跳过重复left
                    right-=1
                    while left<right and nums[right]==nums[right+1]:
                        right-=1  # 跳过重复right

        return ans

优化:

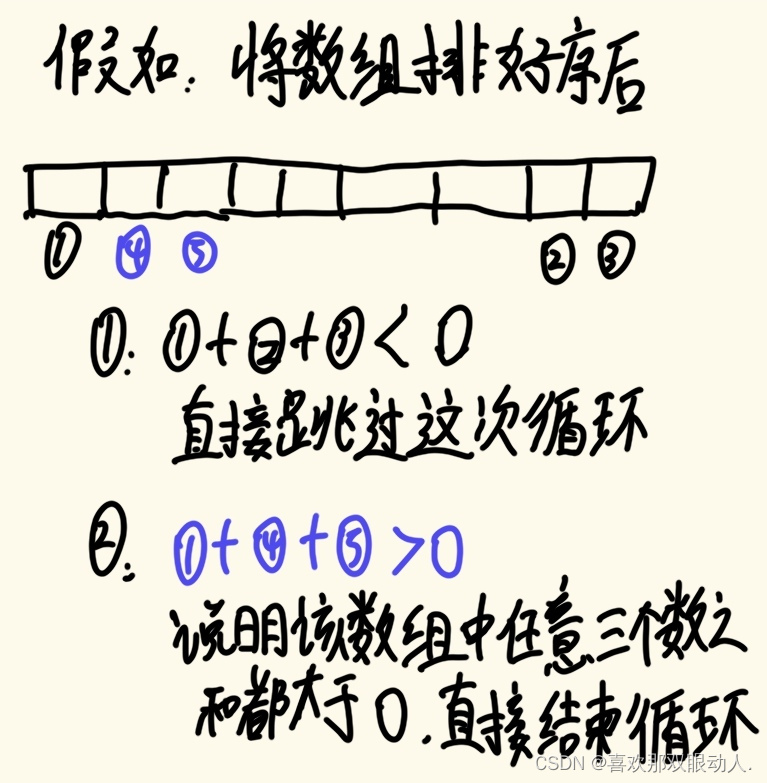
代码:

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        nums.sort()
        ans=[]
        for i in range(len(nums)-2):
            target=nums[i]
            if i>0 and target==nums[i-1]:
                continue
            if target + nums[i + 1] + nums[i + 2] > 0: # 优化(2)
                break
            if target + nums[len(nums)-1] + nums[len(nums)-2]<0: # 优化(1)
                continue
            left=i+1
            right=len(nums)-1
            while left<right:
                if nums[left]+nums[right]+target<0:
                    left=left+1
                elif nums[left]+nums[right]+target>0:
                    right=right-1
                else:
                    ans.append([nums[left], nums[right], target])
                    left+=1
                    while left<right and nums[left]==nums[left-1]:
                        left+=1
                    right-=1
                    while left<right and nums[right]==nums[right+1]:
                        right-=1

        return ans

# 时间复杂度O(n^2)
# 空间复杂度O(n)