FFT学习笔记

FFT（快速傅立叶变换）

向量基本知识

1. 向量加法

$$\begin{gathered} AB=r_1{e}^{i{\theta }_1}=r_1(\cos {\theta }_1+i\sin {\theta }_1) \\ AC=r_2{e}^{i{\theta }_2}=r_2(\cos {\theta }_2+i\sin {\theta }_2) \\ AB+AC=r_1{e}^{i{\theta }_1}+r_2{e}^{i{\theta }_2}=r_1(\cos {\theta }_1+i\sin {\theta }_1)+r_2(\cos {\theta }_2+i\sin {\theta }_2) \\ AB+AC=r_1{e}^{i{\theta }_1}+r_2{e}^{i{\theta }_2}=(r_1\cos {\theta }_1+r_2\cos {\theta }_2)+i(r_1\sin {\theta }_1+r_2\sin {\theta }_2) \end{gathered}$$

2. 向量乘法

   向量乘法可以简单看成向量的旋转和放缩

   

   如图所示最后$AB\times AC=AD$,$i$可以想象成逆时针旋转$90^{\circ }$,所以总结出来 $r_1{e}^{i{\theta }_1}\times r_2{e}^{i{\theta }_2}=r_1{r}_2{e}^{i({\theta }_1+{\theta }_2)}$，

复数的单位根${\omega }_n$

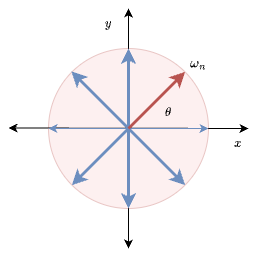
复数的单位根是指满足方程${\omega }^n=1$的复数 $\omega$，其中 $n$是一个正整数。这些根称为 $n$ 次单位根，它们在复平面上均匀分布在单位圆上，形成一个正$n$ 边形的顶点。

满足的性质：

1. ${\omega }^n=1$
2. ${\omega }^{n+k}={\omega }^k$
3. ${\omega }_n^k={\omega }_{2n}^{2k}$
4. ${\omega }_n^{n-k}=\overline{{\omega }_n^k}$ 共轭复数
5. ${\omega }_n^{k+\frac{n}{2}}=-{\omega }_n^k$ ，其实就是逆时针转半圆
6. ${\omega }_n^k+{\omega }_n^{n-k}=Re({\omega }_n^k)$
7. ${\omega }_n^k-{\omega }_n^{n-k}=Im({\omega }_n^k)$

FFT 整体思路

FFT其实就是通过分治策略利用单位根的对称性和周期性加速多项式乘法

• 多项式插值转换：将多项式 ($f(x)={\sum }_{k=0}^{n-1}{a}_k{x}^k$) 在单位根 (${\omega }_n^0,{\omega }_n^1,\dots ,{\omega }_n^{n-1}$) 处求值DFT。

• 分治步骤

  • 偶数项和奇数项分别递归计算：
    $$f(x)=f_{\text{even}}(x^2)+x\cdot f_{\text{odd}}(x^2)$$
  • 利用 (${\omega }_n^{k+n/2}=-{\omega }_n^k$) 合并结果（蝴蝶变换）：
    $$\{\begin{array}{l}f({\omega }_n^k)=f_{\text{even}}({\omega }_{n/2}^k)+{\omega }_n^k\cdot f_{\text{odd}}({\omega }_{n/2}^k)\\ f({\omega }_n^{k+n/2})=f_{\text{even}}({\omega }_{n/2}^k)-{\omega }_n^k\cdot f_{\text{odd}}({\omega }_{n/2}^k)\end{array}$$

多项式乘法
$$f(x)\ast g(x)=a_0{b}_0+\sum _{i=0}^1{a}_i{b}_{1-i}{x}^1+\cdots +\sum _{i=0}^{n+m-2}{a}_i{b}_{n+m-2j},这显然是个O((n+m{)}^2)的算法$$

DFT和IDFT

我们先来看看转化成频域之后会发生什么，将多项式 ($f(x)={\sum }_{k=0}^{n-1}{a}_k{x}^k$) 在单位根 ( ${\omega }_n^0,{\omega }_n^1,\dots ,{\omega }_n^{n-1}$) 处求值
$$\begin{gathered} f(x)=\sum _{k=0}^{n-1}{a}_k{x}^k \\ 设置d_k=\sum _{i=0}^{n-1}{a}_i{\omega }_n^{ki},那么a_k=\sum _{i=0}^{n-1}{d}_k{w}_n^{-ki} \end{gathered}$$

这实际上是线性变换，映射到新的基上，$d_k$其实是基于$n$个基{ωn0,⋯ ,wn(n−1)k}\{\omega_n^0,\cdots,w_n^{(n-1)k}\}{ωn0​,⋯,wn(n−1)k​}表示的一个向量{a0,⋯ ,an−1}\{a_0,\cdots,a_{n-1}\}{a0​,⋯,an−1​}，

那么一共有$n$ 种基
$$W=\left(\begin{array}{cccc}{\omega }_n^0& {\omega }_n^0& \cdots & {\omega }_n^0\\ {\omega }_n^0& {\omega }_n^{1\times 1}& \cdots & {\omega }_n^{(n-1)\times 1}\\ ⋮& ⋮& \ddots & ⋮\\ {\omega }_n^0& {\omega }_n^{1\times (n-1)}& \cdots & {\omega }_n^{(n-1)(n-1)}\end{array}\right)$$

我们要证明的是：

对于 $k\ne l$，这两个向量是正交的：
$$\begin{gathered} \overrightarrow{u_k}=\left[1,{\omega }_n^k,{\omega }_n^{2k},\cdots ,{\omega }_n^{(n-1)k}\right] \\ \overrightarrow{u_l}=\left[1,{\omega }_n^l,{\omega }_n^{2l},\cdots ,{\omega }_n^{(n-1)l}\right] \end{gathered}$$
它们的内积为 0：
$$\begin{array}{rl}⟨\overrightarrow{u_k},\overrightarrow{u_l}⟩& =\sum _{m=0}^{n-1}{\omega }_n^{km}\cdot \overline{{\omega }_n^{lm}}\\ & =\sum _{m=0}^{n-1}{\omega }_n^{km}\cdot {\omega }_n^{-lm}\\ & =\sum _{m=0}^{n-1}{\omega }_n^{(k-l)m}\\ & =\frac{{\omega }_n^n-1}{{\omega }_n-1}=0\end{array}$$
当 $k=l$ 时，显然
$$⟨\overrightarrow{u_k},\overrightarrow{u_k}⟩=\sum _{m=0}^{n-1}{\omega }_n^0=n$$

神奇，因此
$$W{W}^H=n{I}_n$$

因此DFT就是构造了这样一组正交基
$$\left(\begin{array}{c}{d}_0\\ d_1\\ ⋮\\ d_{n-1}\end{array}\right)=\left(\begin{array}{cccc}{\omega }_n^{0\cdot 0}& {\omega }_n^{0\cdot 1}& \cdots & {\omega }_n^{0\cdot (n-1)}\\ {\omega }_n^{1\cdot 0}& {\omega }_n^{1\cdot 1}& \cdots & {\omega }_n^{1\cdot (n-1)}\\ ⋮& ⋮& \ddots & ⋮\\ {\omega }_n^{(n-1)\cdot 0}& {\omega }_n^{(n-1)\cdot 1}& \cdots & {\omega }_n^{(n-1)\cdot (n-1)}\end{array}\right)\left(\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ a_{n-1}\end{array}\right)$$
${\omega }_n=e^{\frac{2\pi i}{n}}$，是 DFT 的单位根,上式就是 DFT 的矩阵乘法形式，$\vec{d}=W\vec{a}$,因此$n\vec{a}=W^H\vec{d}$

用$W^H$求解$\vec{a}$的过程就是DFT的逆变换IDFT

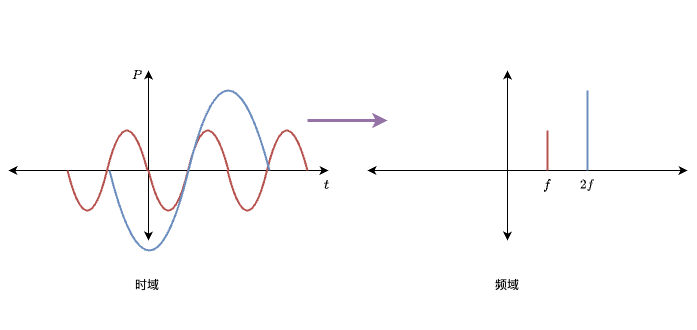
DFT本质上是将输入信号在复平面上进行周期性旋转。不同的旋转角度代表不同的频率成分，这些频率成分合成后就形成了原始信号在频域中的表示。

在IDFT中，频域信号不仅要按相反的方向旋转回去，还需要通过 $\frac{1}{n}$ 进行缩放，这样才能正确地恢复原始信号。每个频率成分在时间域的表示受到频域中其幅度的影响。

题外话

有没有发现这个$W$与范德蒙矩阵很相似。

范德蒙矩阵的一般形式为：
$$V=\left(\begin{array}{ccccc}1& x_0& x_0^2& \cdots & x_0^{n-1}\\ 1& x_1& x_1^2& \cdots & x_1^{n-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& x_{n-1}& x_{n-1}^2& \cdots & x_{n-1}^{n-1}\end{array}\right)$$
范德蒙矩阵可以用来做多项式插值。

多项式乘法

原始时域卷积表达式

多项式乘法对应的是离散卷积：
$$f(x)\cdot g(x)=\sum _{k=0}^{n+m-2}\left(\sum _{j=0}^k{a}_j{b}_{k-j}\right)x^k$$
也就是：
$$c_k=\sum _{j=0}^k{a}_j{b}_{k-j}$$

转化到频域

$$\begin{array}{rl}DFT(c{)}_k& =\sum _{i=0}^{n-1}{c}_i{\omega }_n^{ki}\\ & =\sum _{i=0}^{n-1}\sum _{j=0}^i{a}_j{b}_{i-j}{w}_n^{ik}\\ & =\sum _{i=0}^{n-1}\sum _{j=0}^i(a_j{w}_n^{jk})(b_{i-j}{w}_n^{(i-j)k})\\ & =DFT(a{)}_k\ast DFT(b{)}_k\end{array}$$

因此多项式卷积的频域就是多项式频域点积的积。

实际上就是将全局纠缠的时域操作解耦为局部独立的频域操作

FFT

说了那么多，最后该说FFT了，FFT其实就是利用分治进行DFT操作。

FFT其实就是通过分治策略利用单位根的对称性和周期性加速多项式乘法

• 多项式插值转换：将多项式 ($f(x)={\sum }_{k=0}^{n-1}{a}_k{x}^k$) 在单位根 (${\omega }_n^0,{\omega }_n^1,\dots ,{\omega }_n^{n-1}$) 处求值DFT。

• 分治步骤

  • 偶数项和奇数项分别递归计算：
    $$f(x)=f_{\text{even}}(x^2)+x\cdot f_{\text{odd}}(x^2)$$

  • 利用 (${\omega }_n^{k+n/2}=-{\omega }_n^k$) 合并结果（蝴蝶变换）：
    $$\{\begin{array}{l}{b}_k=f({\omega }_n^k)=f_{\text{even}}({\omega }_{n/2}^k)+{\omega }_n^k\cdot f_{\text{odd}}({\omega }_{n/2}^k)\\ b_{k+\frac{n}{2}}=f({\omega }_n^{k+n/2})=f_{\text{even}}({\omega }_{n/2}^k)-{\omega }_n^k\cdot f_{\text{odd}}({\omega }_{n/2}^k)\end{array}$$

奇偶分组

由于不断要奇偶分组，我们需要把每个数字移动到该有的位置，我们可以进行一个模拟,假设数组的长度为$2^p$

位置$i$的数应该在哪：

最终的位置$pos=0$，很明显可以进行一个递归，如果$i$是奇数，$p=p-1，pos=pos+2^p，i=i/2$ 这明显是对二进制位进行一个反转。

即假设数组长度为$8$, 那么位置$4=0100,pos=0010$，位置$3=0011,pos=1100$,同理，$pos$位置上的数来自于对$pos$二进制的反转。

可以设计一个递推对于一个数字$i$的反转来自于最低位和其他高位即

reverse[i]=reverse[i>>1]>>1+(i&1)<<(p-1)

分治

在进行奇偶分组后，利用变换计算$b_{k+\frac{n}{2}}$ 可以利用分治解决了,为了更清楚的看分治，把式子改写下
$$\begin{gathered} 若l<k<mid，利用对称性和周期性 \\ \begin{array}{rl}{B}_{l,r}[k]& =f_{\text{l,mid}}({\omega }_{mid-l}^k)+{\omega }_n^k\cdot f_{\text{mid,r}}({\omega }_{r-mid}^{k+r-mid})\\ B_{l,r}[k]& =B_{l,mid}[k]+{\omega }_n^k\cdot B_{mid,r}[k+r-mid]\\ B_{l,r}[k+r-mid]& =B_{l,mid}[k]-{\omega }_n^k\cdot B_{mid,r}[k+r-mid]\end{array} \end{gathered}$$

代码

#include<iostream>
#include<vector>
#include<algorithm>
#include<cmath>
using namespace std;
const double PI=acos(-1.0);
struct Complex{
    double x,y;
    Complex():x(0),y(0){};
    Complex(double _x,double _y):x(_x),y(_y){};
    Complex operator-(const Complex &b){return Complex(x-b.x,y-b.y); }
    Complex operator+(const Complex &b){return Complex(x+b.x,y+b.y);}
    Complex operator*(const Complex &b){return Complex(x*b.x-y*b.y,x*b.y+y*b.x);}
    Complex operator/(const double &b){return Complex(x/b,y/b);}
};
vector<int> re,omega;
int len=1;
void init(int n){
    while(len<n) len<<=1;re.resize(len,0);
    for(int i=1,t=(len>>1);i<len;i++) re[i]=((re[i>>1]>>1)|((i&1)?t:0));
}
void move(vector<Complex> &f){for(int i=0;i<len;i++)if(i<re[i]) swap(f[i],f[re[i]]);}
void FFT(vector<Complex> &f,double flag){
    move(f);
    double num=flag?PI:-PI;
    for(int l=2,preL=1;l<=len;preL=l,l<<=1,num/=2){
        Complex wn(cos(num),sin(num));
        for(int j=0;j<len;j+=l){
            Complex w(1,0);
            for(int k=j;k<j+preL;k++){
                Complex u=f[k],v=f[k+preL]*w;
                f[k]=u+v,f[k+preL]=u-v;
                w=w*wn;
            }
        }
    }
    if(flag) for(int i=0;i<len;i++) f[i]=f[i]/len;
}
vector<Complex>a,b;
int main(){
    int n,m;cin>>n>>m;n++;m++;
    init(n+m);
    a.resize(len,Complex(0,0));
    b.resize(len,Complex(0,0));
    for(int i=0;i<n;i++) cin>>a[i].x;
    for(int i=0;i<m;i++) cin>>b[i].x;
    FFT(a,0);
    FFT(b,0);
    for(int i=0;i<len;i++) a[i]=a[i]*b[i];
    FFT(a,1);
    for(int i=0;i<n+m-1;i++) cout<<(int)(a[i].x+0.5)<<" ";cout<<endl;
}

NTT（快速数论变换）-代更

• 上面我们说利用复数单位根来进行加速，复数的单位根是指满足方程$ \omega^n=1$的复数 $\omega$，那么NTT就是利用原根来代替复数单位根。

原根

原根的定义

定义：设正整数$n\ge 2$，整数$g$与$n$互质（即$gcd(g,n)=1$）。如果$g$模$n$的阶等于$\varphi (n)$，则称$g$是模$n$的一个原根。

其中：

• $\varphi (n)$是欧拉函数，表示小于$n$且与$n$互质的正整数的个数
• $g$模$n$的阶是最小的正整数$d$，使得$g^d\equiv 1(\mathrm{mod}n)$