vins博客的一部分5

最新推荐文章于 2024-07-24 17:56:18 发布

原创最新推荐文章于 2024-07-24 17:56:18 发布

· 694 阅读

7 ·

版权

vins 专栏收录该内容

13 篇文章

订阅专栏

initFirstIMUPose（）

得到IUM的Z与重力对齐的旋转矩阵：IMU开始很大可能不是水平放的,重力和Z轴不对齐,用R0对初始IMU坐标系进行旋转,使得Z与g对齐，作为初始位姿Rs[0]（也就是世界系？）。但R0不唯一，我们不想发生围绕Z轴的旋转,即不要动偏航yaw,所以还要再求出yaw的旋转部分,再转回去。

步骤:

输入是accVector,存储了prevTime~curTime的{时间,加速度向量}

首先计算时间段内加速度的均值averAcc，在g2R()中将其归一化，求解到重力方向[0,0,1]的变换矩阵（解不唯一）：

 Matrix3d R0 = Utility::g2R(averAcc)//里面有求解函数R0 = Eigen::Quaterniond::FromTwoVectors(averAcc, g).toRotationMatrix();

这里，默认了初始加速度就是重力加速度，忽略了运动的加速度，需静止初始化。

不想动偏航yaw,所以再求出R0的yaw部分,再转回去：

double yaw = Utility::R2ypr(R0).x();
R0 = Utility::ypr2R(Eigen::Vector3d{-yaw, 0, 0}) * R0;

得到最终的变换矩阵R0,并放到Rs中,作为Rs[0]（Rs存储了各个帧的旋转矩阵）。

processIMU()

预积分
对于每一个新帧，建一个预积分对象pre_integrations[frame_count]。（每两个帧之间都实例化一个IntegrationBase类，构成指针数组pre_integrations的第[frame_count]个指针值）

pre_integrations[frame_count] = new IntegrationBase{acc_0, gyr_0, Bas[frame_count], Bgs[frame_count]}//以这个帧间第一个imu测量作为初始值new

将本次输入到函数中的IMU测量量acc\gry,做中值积分,累加到delta_p\v\q，详见propagate

// 对传入的两个相邻的imu测量量进行一次预积分
pre_integrations[frame_count]->push_back(dt, linear_acceleration, angular_velocity);//进去主要就是propagate()

积分
还对两帧间所有的imu进行了积分，其值存在Rs[frame_count],Ps[frame_count],Vs[frame_count]中：
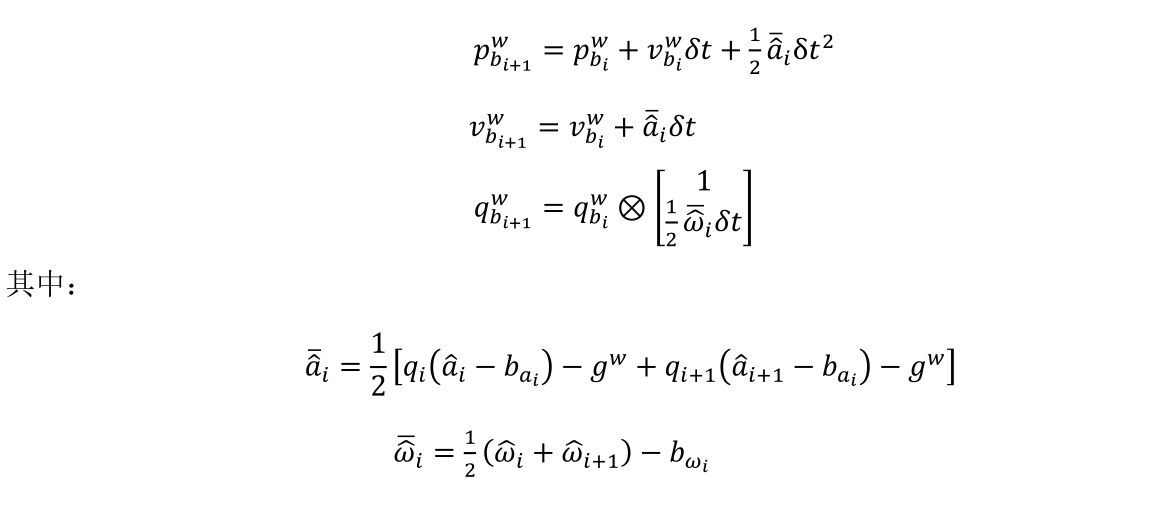
在这里插入图片描述

Vector3d un_acc_0 = Rs[j] * (acc_0 - Bas[j]) - g;
Vector3d un_gyr = 0.5 * (gyr_0 + angular_velocity) - Bgs[j];
Vector3d un_acc_1 = Rs[j] * (linear_acceleration - Bas[j]) - g;
Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);

Rs[j] *= Utility::deltaQ(un_gyr * dt).toRotationMatrix();
Ps[j] += dt * Vs[j] + 0.5 * dt * dt * un_acc;
Vs[j] += dt * un_acc;

IMU预积分结果在delta_p\v\q，是帧间的增量，用来优化。
IMU积分结果在Rs Ps Vs，是两帧间的位姿变化量，用来做用图像求解位姿的初值。

propagate()

主要就是种中值分midPointIntegration()这一句

midPointIntegration(_dt, acc_0, gyr_0, _acc_1, _gyr_1,//本时刻的瞬时值,和上一时刻的瞬时值
                    delta_p, delta_q, delta_v,//累计的位移\角速度\速度
                    linearized_ba, linearized_bg,//偏移
                    result_delta_p, result_delta_q, result_delta_v,//本次累计后结果
                    result_linearized_ba, result_linearized_bg, 1);//偏移,直接就是上面传递进来, 1 为更新雅克比

其中midPointIntegration()干了两件事：

1、中值积分

本次相对初帧值的加速度矢量 = 之前角度累计变化量 * 加速度a1

上一次相对初帧值的加速度矢量 = 之前角度累计变化量 * 加速度a0

本次时间间隔内的加速度矢量, 1/2 * (初 + 末)

本次时间间隔内的角速度矢量， 1/2 * (初 + 末)

角度累计变化量:用四元数表示求得 = 之前变化δQ * 本次变化δq(四元数,每个方向为w*dt/2)

速度累计变化量: δV + δv * dt

加速度累计变化量:δP + δV * dt + 0.5 * a * t^2

在这里插入图片描述

Vector3d un_acc_0 = delta_q * (_acc_0 - linearized_ba);
Vector3d un_acc_1 = result_delta_q * (_acc_1 - linearized_ba);
Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);
Vector3d un_gyr = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg;
result_delta_p = delta_p + delta_v * _dt + 0.5 * un_acc * _dt * _dt; 
result_delta_v = delta_v + un_acc * _dt;
result_delta_q = delta_q * Quaterniond(1, un_gyr(0) * _dt / 2, un_gyr(1) * _dt / 2, un_gyr(2) * _dt / 2);

2、更新雅克比
在这里插入图片描述先由公式,得到矩阵 $F\ V$ :

// F
MatrixXd F = MatrixXd::Zero(15, 15);
F.block<3, 3>(0, 0) = Matrix3d::Identity();//左上角的I
F.block<3, 3>(0, 3) = -0.25 * delta_q.toRotationMatrix() * R_a_0_x * _dt * _dt + 
	-0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - 		R_w_x * _dt) * _dt * _dt;//f01
F.block<3, 3>(0, 6) = MatrixXd::Identity(3,3) * _dt;//f02
F.block<3, 3>(0, 9) = -0.25 * (delta_q.toRotationMatrix() + 					 	   	 result_delta_q.toRotationMatrix()) * _dt * _dt;//f03
F.block<3, 3>(0, 12) = -0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * 		_dt * -_dt;//f04
......
// V
MatrixXd V = MatrixXd::Zero(15,18);
V.block<3, 3>(0, 0) =  0.25 * delta_q.toRotationMatrix() * _dt * _dt;//v00
V.block<3, 3>(0, 3) =  0.25 * -result_delta_q.toRotationMatrix() * R_a_1_x  * _dt * 	_dt * 0.5 * _dt;//v01
V.block<3, 3>(0, 6) =  0.25 * result_delta_q.toRotationMatrix() * _dt * _dt;//v02
V.block<3, 3>(0, 9) =  V.block<3, 3>(0, 3);//v03
......

利用下式，对两帧间预积分的雅可比和协方差不断更新（ $J 、 P$ 其初值分别为 $I 、 0$ ， $Q$ 的初值为噪声方差构成的矩阵 $diag(σ^2...)$ ）：
在这里插入图片描述

jacobian.setIdentity();//本帧刚进入时，初始化
covariance.setZero();

jacobian = F * jacobian;//更新
covariance = F * covariance * F.transpose() + V * noise * V.transpose();

在优化中，就求解 $B a 、 B g$ 用到这里的雅可比和协方差了。
midPointIntegration()至此完成。

然后,将midPointIntegration()返回结果从result_delta_p\v\q放回delta_p\v\q；
偏置直接相等linearized_b = result_linearized_b；
并把四元数q归一化（运算后可能模不为1）；
最后把本次时间dt累加进sum_dt。
更新加速度角速度值,等待下次积分