回溯法、DFS、递归、栈、BFS知识点总结

我是真的菜啊啊

已于 2023-03-14 10:25:51 修改

阅读量848

点赞数 1

分类专栏： LeetCode 文章标签： leetcode 算法

于 2022-10-23 20:05:45 首次发布

本文链接：https://blog.youkuaiyun.com/qq_42671928/article/details/127479600

版权

LeetCode 专栏收录该内容

35 篇文章

订阅专栏

本文详细解析了深度优先搜索（DFS）与回溯算法的区别，指出回溯是在DFS基础上增加状态重置以寻找所有解。文章通过子集、组合及全排列问题的实例，展示了如何编写回溯算法，强调了状态变量、结束条件、选择列表和剪枝的重要性。此外，还探讨了在不同问题中如何选择使用used数组或begin变量。最后，通过两个具体的组合问题实例（组合总和I和II）进一步阐述了回溯法的运用策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. DFS 和回溯算法区别

DFS 是一个劲的往某一个方向搜索，而回溯算法建立在 DFS 基础之上的，但不同的是在搜索过程中，达到结束条件后，恢复状态，回溯上一层，再次搜索。因此回溯算法与 DFS 的区别就是有无状态重置

2. 何时使用回溯算法

当问题需要 "回头"，以此来查找出所有的解的时候，使用回溯算法。即满足结束条件或者发现不是正确路径的时候(走不通)，要撤销选择，回退到上一个状态，继续尝试，直到找出所有解为止

3. 怎么样写回溯算法(从上而下，※代表难点)

①画出递归树，找到状态变量(回溯函数的参数)，这一步非常重要※
②根据题意，确立结束条件
③找准选择列表(与函数参数相关), 与第一步紧密关联※
④判断是否需要剪枝
⑤作出选择，递归调用，进入下一层
⑥撤销选择

4. 回溯问题的类型（三种）

（子集、组合）、全排列、搜索

A、子集 - 给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        backtrack(nums, res, 0, new ArrayList<Integer>());
        return res;
    }
    
    private void backtrack(int[] nums, List<List<Integer>> res, int start, ArrayList<Integer> tmp) {
        res.add(new ArrayList<>(tmp));
        for(int i = start; i < nums.length; i++) {
            tmp.add(nums[i]);
            backtrack(nums, res, i + 1, tmp);
            tmp.remove(tmp.size() - 1);
        } 
    }
}

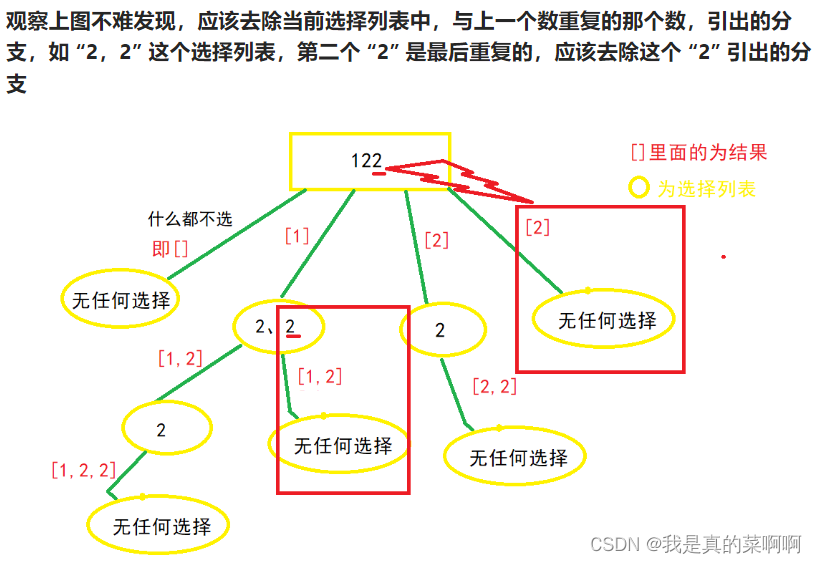
B、子集 II(剪枝思想)

class Solution {
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        List<List<Integer>> res = new ArrayList<>();
        backtrack(nums, res, 0, new ArrayList<>());
        return res;
    }
    private void backtrack(int[] nums, List<List<Integer>> res, int start, ArrayList<Integer> tmp) {
        res.add(new ArrayList<>(tmp));
        for(int i = start; i < nums.length; i++) {
            if(i > start && nums[i] == nums[i-1]) {  //同一层级不出现相同元素；允许不同层级出现相同元素
                continue;
            }else {
                tmp.add(nums[i]);
                backtrack(nums, res, i + 1, tmp);
                tmp.remove(tmp.size() - 1);
            }
        }
    }
}

C、组合总和

方法一、回溯法

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        List<List<Integer>> res = new ArrayList<>();
        backtrack(candidates, res, 0, 0, target, new ArrayList<>());
        return res;
    }
    private void backtrack(int[] nums, List<List<Integer>> res, int start, int sum, int target, ArrayList<Integer> tmp) {
        if(sum == target) {  //满足条件
            res.add(new ArrayList<>(tmp));
            return ;
        }
        for(int i = start; i < nums.length; i++) {
            if(sum > target) {  //剪枝
                continue;
            }
            tmp.add(nums[i]);
            backtrack(nums, res, i, sum + nums[i], target, tmp);
            tmp.remove(tmp.size() - 1);
        }
    }
}

方法二：

import java.util.*;

public class Solution {

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> res = new ArrayList<>();
        if (len == 0) {
            return res;
        }
        // 排序是剪枝的前提
        Arrays.sort(candidates);
        //初始化栈
        Deque<Integer> path = new ArrayDeque<>();
        int begin = 0;  //起始位点
        
        dfs(candidates, begin, len, target, path, res);
        return res;
    }

    private void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> res) {
        // 由于进入更深层的时候，小于 0 的部分被剪枝，因此递归终止条件值只判断等于 0 的情况
        if (target == 0) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = begin; i < len; i++) {
            // 重点理解这里剪枝，前提是候选数组有序，
            if (target - candidates[i] < 0) {
                break;
            }
            path.addLast(candidates[i]);
            dfs(candidates, i, len, target - candidates[i], path, res);
            path.removeLast();
        }
    }
}

总结：子集、组合类问题，关键是用一个 start 参数来控制选择列表！！

回溯六步：

①画出递归树，找到状态变量(回溯函数的参数)，这一步非常重要※
②根据题意，确立结束条件
③找准选择列表(与函数参数相关),与第一步紧密关联※
④判断是否需要剪枝
⑤作出选择，递归调用，进入下一层
⑥撤销选择

backtrack的公式：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

组合问题

什么时候使用 used 数组，什么时候使用 begin 变量
排列问题，讲究顺序，需要记录哪些数字已经使用过，此时用 used 数组；
组合问题，不讲究顺序，需要按照某种顺序搜索，此时使用 begin 变量。

40. 组合总和 II

class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> res = new ArrayList<>();
        if(len == 0){
            return res;
        }
        Arrays.sort(candidates);  // 先排序以使用剪枝
        Deque<Integer> path = new ArrayDeque<>();
        int begin = 0;
        dfs(candidates, begin, len, target, path, res);
        return res;
    }

    private void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> res){
        //大剪枝，
        if(target == 0){
            res.add(new ArrayList<>(path));
            return;
        }

        for(int i = begin; i < len; i++){
            // 小剪枝：同一层相同数值的结点，从第 2 个开始，候选数更少，结果一定发生重复，因此跳过，用 continue
            if (i > begin && candidates[i] == candidates[i - 1]) {
                continue;
            }
            if(target - candidates[i] < 0){
                break;
            }
            path.add(candidates[i]);
            dfs(candidates, i + 1, len, target - candidates[i], path, res);
            path.removeLast();
        }
       
    }
}

46. 全排列

47. 全排列 II