HDU1576-A/B(逆元模板)

最新推荐文章于 2022-11-15 23:11:24 发布

原创最新推荐文章于 2022-11-15 23:11:24 发布 · 159 阅读

1 ·

CC 4.0 BY-SA版权

数学==杜教筛/莫比乌斯/积性函数/欧拉等数论专栏收录该内容

32 篇文章

订阅专栏

本文介绍了一种高效的模逆元批量求解方法，利用扩展欧几里得算法预处理模逆元，显著提高了大范围数值的逆元计算效率。通过对比单次求解，该方法在处理大量数据时优势明显，适用于竞赛编程和大规模计算任务。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

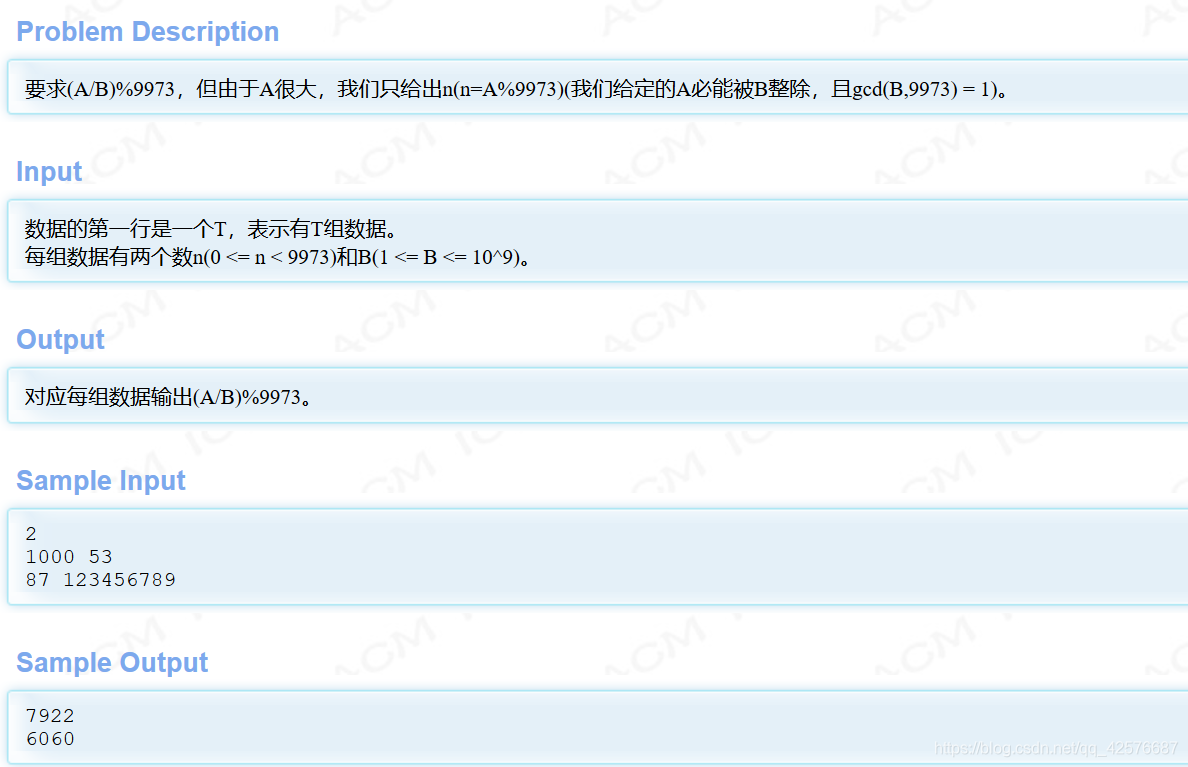
题目
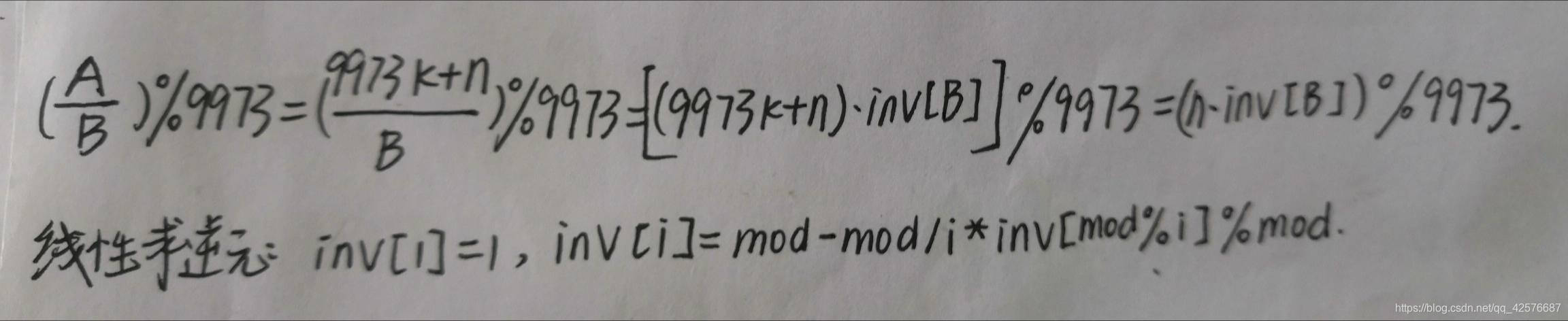
在这里插入图片描述

#include<iostream>
#define en '\n'
using namespace std;
typedef long long ll;
const ll mod=9973;
void ex_gcd(ll a,ll b,ll &x,ll &y)
{
    if(!b){
        x=1,y=0;
        return;
    }
    ex_gcd(b,a%b,x,y);
    ll r=x;
    x=y,y=r-a/b*y;
}
int main()
{
    int T;scanf("%d",&T);
    ll x,y;
    while(T--)
    {
        ll n,B;scanf("%lld%lld",&n,&B);
        B%=mod;
        ex_gcd(B,mod,x,y);
        x=(x+mod)%mod;
        printf("%lld\n",n*x%mod);
    }
}

#include<iostream>
#define en '\n'
using namespace std;
typedef long long ll;
const int N=1e4+5;
const ll mod=9973;
ll inv[N];
ll niyuan(ll x)
{
    if(x<=N-5) return inv[x];
    return mod-mod/x*niyuan(mod%x)%mod;
}
void init()
{
    inv[1]=1;
    for(int i=2;i<=N-5;++i)
        inv[i]=mod-mod/i*inv[mod%i]%mod;
}
int main()
{
    init();
    int T;scanf("%d",&T);
    while(T--)
    {
        ll n,B;scanf("%lld%lld",&n,&B);
        B%=mod;//x*inv[x]%mod=1,(k*mod+x)*inv[x]%mod=1;
        printf("%lld\n",n*niyuan(B)%mod);
    }
}