吴恩达神经网络和深度学习-学习笔记-15-局部最优

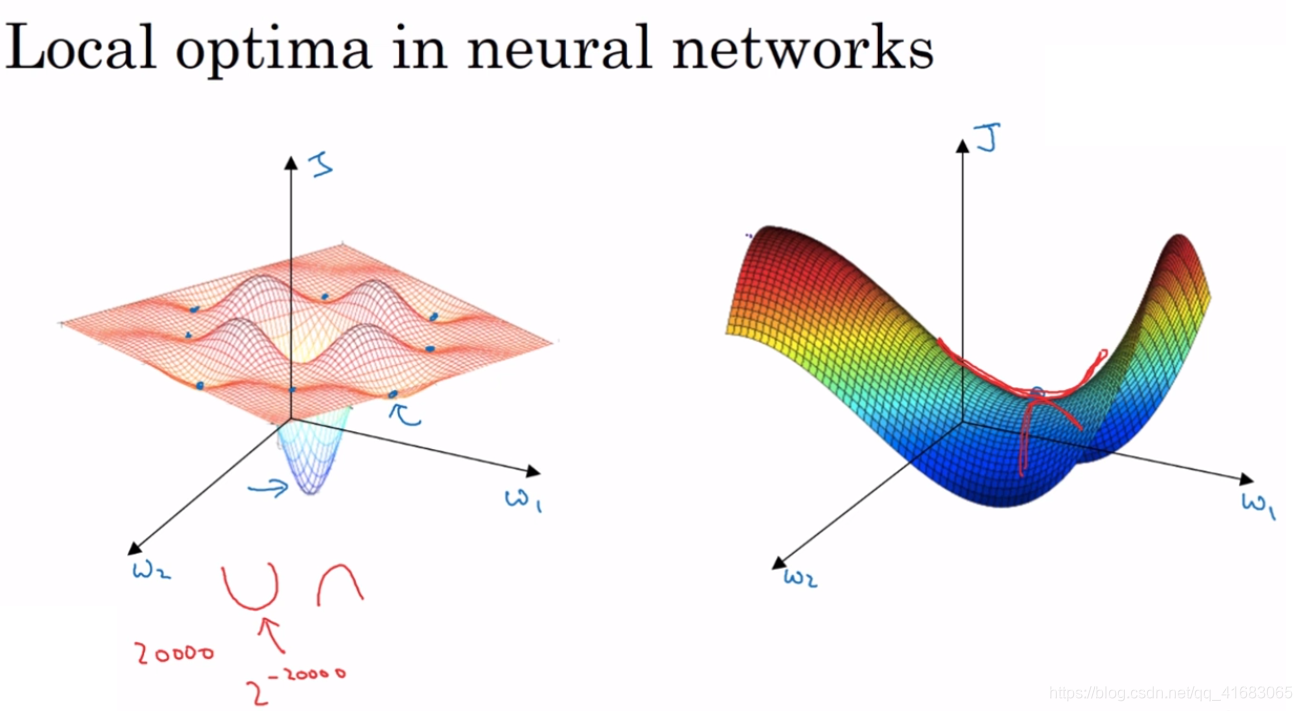
左图为我们对于低维空间的想象，似乎局部最优广泛存在。梯度下降法或者某个算法可能困在一个局部最优中，而不会抵达全局最优。
但这些理解并不正确
事实上如果我们要创建一个神经网络，通常梯度为0的点并不是左图中的局部最优点。实际上成本函数的零梯度点通常是鞍点。
因为一个具有高维空间的函数，如果梯度为0，那么在每个方向，它可能是凸函数也可能是凹函数。如果在20000维空间中想要得到局部最优，发生概率为2^-20000，是一个非常非常小的值。明显遇到鞍点的概率要大得多。

我们对于低维空间的大部分直觉，并不能应用到高维空间中

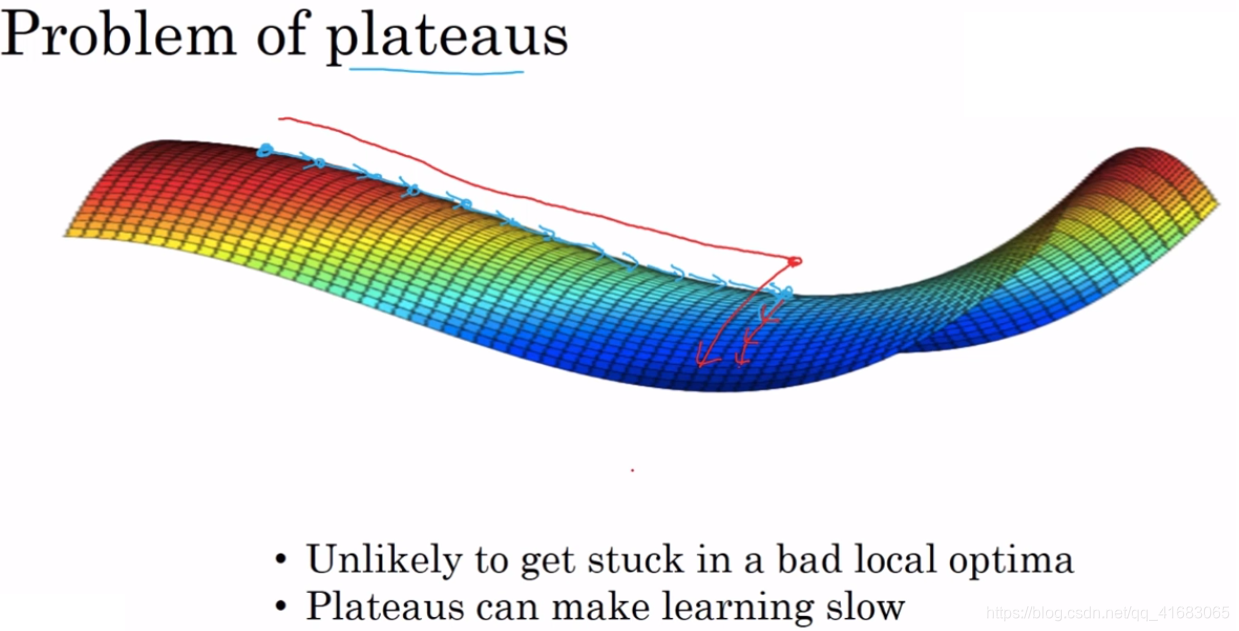
第一：我们不太可能困在局部最优值中。
第二：平稳段会减慢学习速度（平缓段导数长时间趋于0）。