吴恩达神经网络和深度学习-学习笔记-11-Momentum梯度下降法

Momentum的原理

这个算法肯定要好于没有Momentum的梯度下降算法（This will almost always work better than the straightforword gradient descent algorithm without momentum）。
Momentum梯度下降法的基本思想是：计算梯度的指数加权平均数，并用该梯度更新你的权重。

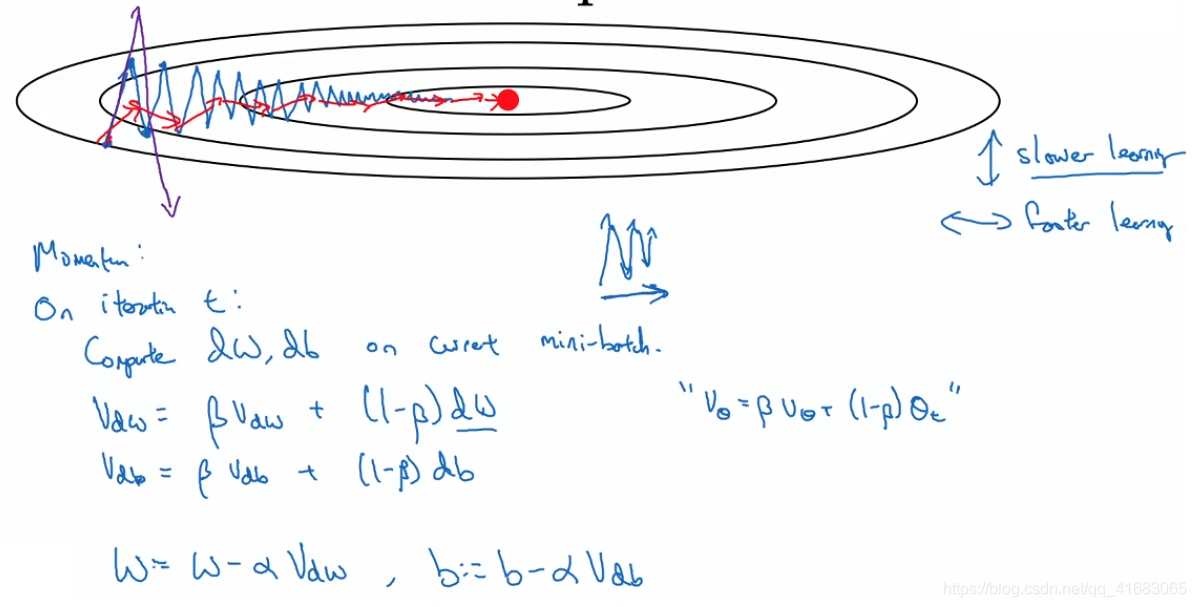
在常规梯度下降算法（batch梯度下降法、mini-batch梯度下降法）中，在合适的学习率（比较小）的情况下，会沿蓝线找到最小值。当学习率过大时会变成紫色。
而我们希望它在纵轴上变化小一点，在横轴上变化大一点。
这样我们借用指数加权平均法来实现。（公式见图片）
纵轴的正负在求和平均后相互抵消，横轴在求和平均后依旧较大，便得到红线的结果。
因此用算法几次迭代后，你发现Momentum梯度下降法最终纵轴方向的摆动变小了，横轴方向运动更快。也就是算法走了一条更加直接的路径，在抵达最小值的路上减小了摆动。

Momentum的一个本质，就是它们能最小化碗状函数。

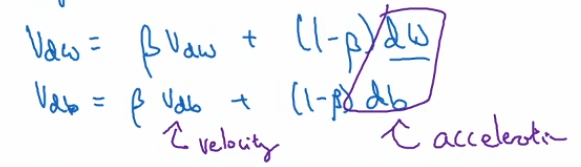
这些微分项dW, db可以被想象为从山上往下滚的球，提供了加速度 ，Momentum项就相当于速度。所以想象你有一个碗，再拿一个球，微分给了这个球一个加速度，球因为加速度越滚越快，而因为β稍小于1从而表现出一些摩擦力，所以球不会无限加速下去。
所以不像梯度下降法的每一步都独立于之前的步骤，你的球可以向下滚，获得动量。

Momentum的实现

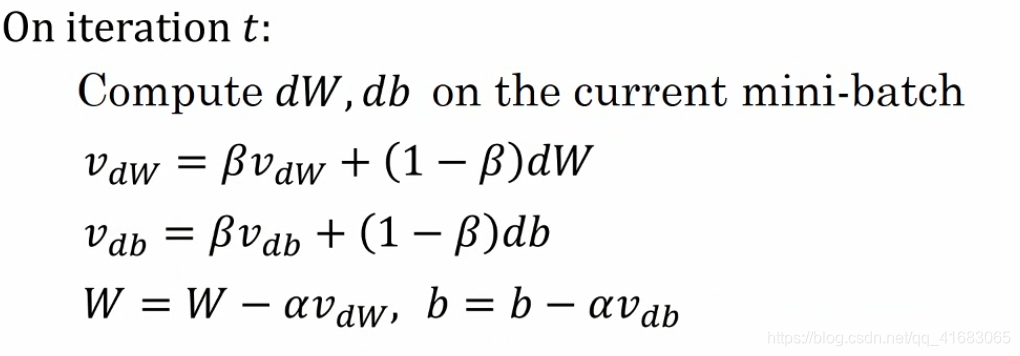
初始v_dW和v_db均为0。

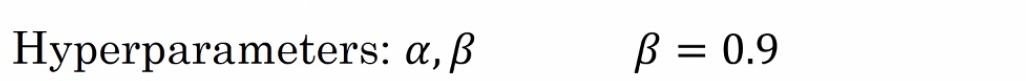
我们有两个超参数：学习率α和指数加权平均数参数β。其中β最常用的值是0.9（works very well），是个不错的鲁棒值。而且在实际中并不用偏差修正，因为10次迭代之后（移动距离超过了初始阶段）就不再是一个有偏差的预测。
实际中，在使用梯度下降法或Momentum时，人们不会收到偏差修正的困扰。