4. tereo Systems and Structure from Motion【cs231a课程笔记】

同系列链接

1. pinhole camera model【cs231a课程笔记】
2. Single View Metrology【cs231a课程笔记】
3. epipolar geometry【cs231a课程笔记】
4. tereo Systems and Structure from Motion【cs231a课程笔记】
5. Active and Volumetric Stereo【cs231a课程笔记】

4.1. tereo Systems and Structure from Motion

Triangulation三角剖分

已知两个相机内外参K，K‘，相机位置关系R，T，三维中的P投影为p和p’。

首先用$O_{1}p$和$O_2{p}^{\prime }$求出$l和l^{\prime }$,两线角点就是P

但是这个方法对p，p‘，$O_1,O_2$的精度要求太高，一般预测P不准确，甚至有时两线不相交。

4.2. Triangulation三角剖分

4.2.1. linear method for triangulation

用两个点$p=MP=(x,y,1)$，$p‘=M’P=(x’,y‘,1)$，

所以$p\times (MP)=0$，外积得0，写成下面的形式

化简为$AP=0$，A等于：

可以用SVD求解P点的最优估计

但这个方法不适用于projective reconstruction（投影重建），因为SVD要求||P||=1，但在投影变换中，P不是一个投影不变量。所以虽然简单，但通常不是三角剖分问题的最优解

4.2.2. nonlinear method for triangulation

非线性方法就是最优化下面的问题

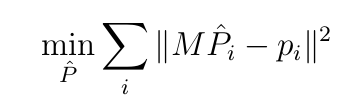
$\hat{P}$是P的预测，最小化在两（多）个图片上的reprojectoin error重投影误差
sophisticated复杂

对于这种非线性最小二乘优化问题，有很多复杂技巧，但本课程只讲一个——Gaus-Newton算法。

非线性最小二乘优化问题通常表示（$x\in R^n$）：

$r_i(M{)}^2=||M{\hat{P}}_i-p_i|{|}^2$
r是residual function残差方程：$R^n\to R^m$,$r(x)=f(x)-y$.f（x）是线性，就是线性优化，反之亦然。

投影变换一般都是非线性，因为包含了齐次坐标系的一个维度。

如果将$e_i$设为2x1的向量$e_i=M{\hat{P}}_i-p_i$，则有

用Gauss-Newton算法找最优解，关键思想是通过迭代找估计解$\hat{P}$,每一次迭代用一个更新值${\delta }_P$:$\hat{P}=\hat{P}+{\delta }_P$,又有（e()为error）：

最小化问题转化为:

对于N张图片，我们有

其中

每一个$e_i$都是2x1的向量，因为有两个维度x，y，所以e的维度是2Nx1

可以设立一个固定的值充当迭代的遍数

4.3. Affine structure from motion

SFM可以同时确定3D结构和相机参数

下面是基本模型，M是内外参

首先，我们只考虑仿射，简单些

所以对于M，v=0

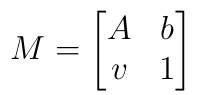
就有：

我们可以进一步简化

然后可以用$M_{affine}=[Ab]$表示所有的仿射中的相机参数

我们可以发现，需要预测m个M矩阵，n个X三维坐标，一共8m+3n个未知量，有mn观测量，买个观测量有2个限制方程，一个2mn个限制方程。所以，当2mn>=8m+3n时，才有确定解。

那么当我们有足够的点时，该怎么解呢

4.3.1. The Tomasi and Kanade factorization method

因子分解法主要有两步，第一步是数据集中（centering），第二步才是因子分解

第一步：
我们定义

j是不同点的标号，i是不同相机的标号

由之前的关系又有：

于是有：

第二步：
我们有：

又因为D是M（2mx3）和S（3xn）的乘积，所以rank(D)=3

为了，将D分解为M和S，我们用SVD, $D=U\Sigma V^T$.所以：

虽然实际中rank(D)>3,由于噪声的存在，但这个结果依然是MS的最优估计

那么具体M和S是什么呢，在两人的论文中，给出了一个取中的解：

4.3.2. Ambiguity in reconstruction

我们选择用一个3x3的矩阵A，替换$\Sigma$:

所以解不是确定的，我们要通过更多的限制条件解。

我们需要标定板上的已知大小，去确定A

4.4. Perspective structure from motion

一般情况（映射变换）

类似于affine的情况，我们有2mn个限制方程，有11m+3n-15个未知量。

15是因为相机和点只能恢复到4x4的投影变换？

4.4.1. The algebraic approach

leverage 杠杆作用，利用
canonical(最简洁的) matrix 规范矩阵（对角线元素只能是0,1,-1）
geometrical interpretation 几何解释

该方法利用基本矩阵F解决相机之间的运动问题
有一个投影变换H，使得：

首先计算基本矩阵F，定义$\tilde{P}=HP$，有：

可以推出

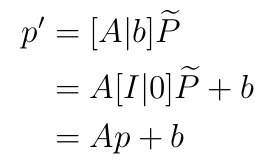
我们做cross product 叉乘

又由于$p^{\prime }\times b$垂直与$p^{\prime }$，有：

又由于$p^{\prime T}Fp=0$，所以

我们计算Fb

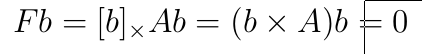
发现等于0,由于F是奇异的，b是一个最小二乘解，当$||b||=1$，用SVD

b知道后，可以计算A，$A=-[b{]}_{X}F$，证明

所以，我们重新定义$M_1{H}^{-1},M_2{H}^{-1}$

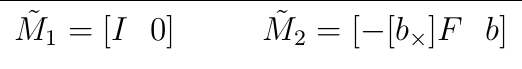
接下来我们给出b的几何解释，在对极几何里，我们有极点与基本矩阵F点积为0,$F{e}_2=0,F^T{e}_1=0$,所以，b也是一个极点。所以上式有另一种形式

4.4.2. Determining motion from the Essential matrix

skew-symmetric 斜对称

更精确的方式是用本质矩阵，假设我们知道了相机的内参K

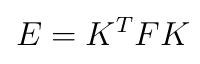
可以由旋转矩阵R和平移向量t表示：

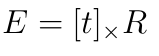
我们定义两个将会在分解时用到的矩阵

有几个特性


作为特征值分解的结果，我们可以创建按比例缩放的一般斜对称矩阵的块分解，所以，我们可以有

所以E：

因为E的特征值分解结果$E=U\Sigma V^T=Udiag(1,1,0)V^T$，所以

证明：R的特征值分解只能是$R=UX{Y}^T$，有$ZX=diag(1,1,0)$，所以$X=W或W^T$

为了保证R是一个旋转矩阵，所以(det是行列式):

类似于R，t可能取几个值，我们已经知道

U是酉矩阵（unitary matrix https://blog.youkuaiyun.com/sayaitachi/article/details/77749613），我们发现$||[t{]}_X|{|}_F=\sqrt{2}$，由于上诉的等式及E按比例已知，我们有

一共有四种可能，但只有a点在两相机同侧。

一般来讲，我们只需三角剖分一个点，就可得到R，T，但因为噪声误差，实际用多个点。

4.5. An example structure from motion pipeline

up to scale：只差一个比例因子（不知道像素点与实际大小的关系）

4.5.1. Bundle adjustment（光束平差法 BA）

factorization method分解法 假设所有点都是可见的

后来用代数方法，但不能解决使用所有摄像机和3D点进行连贯优化的重建的问题。

用BA——SFM的非线性方法可以克服困难。

最小化重投影误差，只需要可见点（不需要所有点）

常见算法有Gauss-Newton算法，Levenberg-Marquardt算法

对初始条件要求高（否则可能到局部最优，或不收敛），所以一般接在其他方法后面。