1. pinhole camera model 小孔相机模型【cs231a课程笔记】

同系列链接

1. pinhole camera model【cs231a课程笔记】
2. Single View Metrology【cs231a课程笔记】
3. epipolar geometry【cs231a课程笔记】
4. tereo Systems and Structure from Motion【cs231a课程笔记】
5. Active and Volumetric Stereo【cs231a课程笔记】

1.1. pinhole camera model

数码相机的镜头相当于一个凸透镜 + 小孔成像

理想化的相机模型是线性模型（实际是非线性模型）：

retinal plane 视网膜平面
camera coordinate system（camera reference system）摄像机坐标系
camera calibration 相机标定

将三维摄像机坐标系中的P点映射到二维image plane中的P’

pinhole（center of the camera）：$O$
focal length： $f$
$O{C}^{\prime }$称作optical axis 光轴

$P[x,y,z{]}^T$转化到$P^{\prime }[x^{\prime },y^{\prime }{]}^T$

相似三角形$P^{\prime }{C}^{\prime }O$和$PO(0,0,z)$

$P^{\prime }=[x^{\prime },y^{\prime }{]}^T=[f\ast x/z,f\ast y/z{]}^T$

aperture size越大，成像越模糊，越亮

所以 小aperture + lenses(透镜)

1.2. lens-based model (paraxial refraction model)

(凸)透镜相机模型（轴旁折射模型）

只有$P$点所在的平面（焦平面）是清晰的（in focus），有了焦距（景深）的概念

$P^{\prime }=[x^{\prime },y^{\prime }{]}^T=[z^{\prime }\ast x/z,z^{\prime }\ast y/z{]}^T$

上式依据：对于焦平面上的点，$P{P}^{\prime }$过透镜中心$O$点

distortion

radial distortion(径向畸变):
pincushion distortion(枕形畸变) and barrel distortion(桶形畸变)

1.3. digital image space

加上image plane（film）(原点在k轴和平面交点处，一般是图片中心点）和image（原点在图片左下角）之间的关系C

$P^{\prime }=[x^{\prime },y^{\prime }{]}^T=[z^{\prime }\ast x/z+c_x,z^{\prime }\ast y/z+c_y{]}^T$

加上现实距离和像素距离之间的关系$k,l=pixeks/cm$，若$k=l$，则相机有正方形像素。

$P^{\prime }=[x^{\prime },y^{\prime }{]}^T=[z^{\prime }\ast k\ast x/z+c_x,z^{\prime }\ast l\ast y/z+c_y{]}^T=[\alpha \ast x/z+c_x,\beta \ast y/z+c_y{]}^T$

homogeneous coordinate system 齐次坐标系

我们认为欧式空间中的（x，y，z）等价于齐次坐标系中的（x，y，z，1），所以我们认为齐次坐标系$(v_1,...,v_n,w)$等价于欧式空间$(v_1/w,...,v_n/w)$

$I$ 是 3×3
$K$ 是camera matrix
上式中不包含skewness（倾斜）和dissortion（畸变）

下图中加入skewness,其中$\theta$是坐标系夹角与90度的差

大多数本课程讲述的方法忽略了distortion，故最终final camera matrix有5个自由度：
2个关于focal length: $\alpha ,\beta$
2个关于offset: $c_x,c_y$
1个关于skewness: $\theta$

1.4. an arbitrary world reference system to image plane

before：将三维摄像机坐标系映射到二维image plane

加入选择矩阵 rotation matirx R和平移向量 tranlation vector T

与之前结合化简

M中包含了intrinsic和extrinsic参数，K是内参，[R, T]是外参。

M有11个自由度，5个内参自由度，3个外参（旋转），3个外参（平移）

1.5. Camera Calibration

用images推断内参

deduce 推断
calibration rig 标定台

$p_i$是照片中的i点，$P_i$是3D空间中的点，m1,m2,m3是M的三行（欧式空间和齐次坐标系变换）


对于n个图片，写成矩阵形式：

trivial solution平凡解
overdetermined过定的（含有线性相关的两列）
scalar标量

用SVD（分解奇异值）：$P=UD{V}^T$，$V^T$与m合并为某常数乘M，约束条件变为$|M|=|V^{T}m|=|V^T||m|=1$(单位正交阵的行列式为1或-1)

进一步有

解得

退化形态（degeneration configuration）：
不是所有情况都能有解，比如图片都在一个平面上（线性无关的方程数量小于未知数数量（11））

1.6. Handling Distortion in Camera Calibration

通常畸变是对称的，以为透镜是对称的，所以用一个isotropic transformation（各向同性变换）表示

变换一下：

但这不是线性的，我们可以寻找其他办法（比如利用比值（不变的））



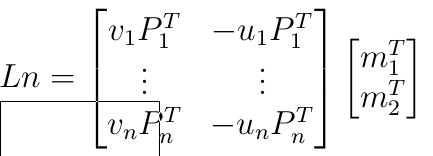
可以使用SVD求解（类似上面）

求出m1,m2,再用$\lambda$可以求m3,仍然是非线性优化问题，但简单很多

1.7. Rigid Transformations

rotation，translation，sacling