AVL树成功失败:
https://blog.youkuaiyun.com/qq_38998213/article/details/83447989
霍夫曼树(哈夫曼):每个节点要嘛没有子节点,要么有两个子节点。 带权路径长度:WPL。
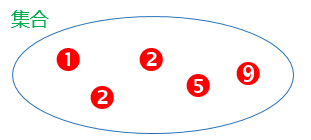
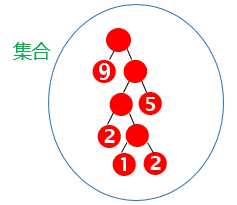
WPL = 1*9 + 2*5 + 3*2 + 4*1 + 4*2 =37
另外还可以有另外一个方法,结合算法描述仔细观察发现最小带权路径长度为非叶子结点的和 ,即
霍夫曼树(哈夫曼):每个节点要嘛没有子节点,要么有两个子节点。 带权路径长度:WPL。


WPL = 1*9 + 2*5 + 3*2 + 4*1 + 4*2 =37
另外还可以有另外一个方法,结合算法描述仔细观察发现最小带权路径长度为非叶子结点的和 ,即
 5561
5561
 1038
1038
 5838
5838
 7104
7104

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


