复数是什么，傅里叶变换，拉普拉斯

已于 2024-01-29 13:33:27 修改
阅读量362 收藏
点赞数 1
CC 4.0 BY-SA版权
分类专栏： 2020数学 2021 AI paddle 文章标签： python
于 2021-11-15 22:01:25 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_38998213/article/details/121344277
本文介绍了复数的概念，包括虚数单位i及其在加法和乘法中的作用。接着，讨论了傅里叶变换，它是将函数分解为正弦波叠加的过程。然后，重点转向拉普拉斯变换，它解决了傅里叶变换中处理衰减问题的局限，通过衰减因子来处理无穷大函数，并探讨了其收敛域和特殊傅里叶变换的情况。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

目录

复数是什么

傅里叶变换

将函数拆解成一堆正弦波的叠加

拉普拉斯变换：函数无穷大问题（在傅里叶基础上 * 衰减因子）​

拉普拉斯：

衰减因子和原函数绑定 ：将无穷大掰弯

衰减因子和后面函数绑定 ：震荡变大​​

收敛域​

拉普拉斯特殊的傅里叶变换（衰减因子是1）​

拉普拉斯变换

复数是什么

虚数 i 就是逆时针旋转90度，i 不是一个数，而是一个旋转量

因此，我们可以得到下面的关系式：

　　(+1) * (逆时针旋转90度) * (逆时针旋转90度) = (-1)

如果把+1消去，这个式子就变为：

　　(逆时针旋转90度)^2 = (-1)

将"逆时针旋转90度"记为 i ：

　　i^2 = (-1)

所以，我们可以知道，虚数 i 就是逆时针旋转90度，i 不是一个数，而是一个旋转量。

虚数的作用：加法

虚数的引入，大大方便了涉及到旋转的计算。

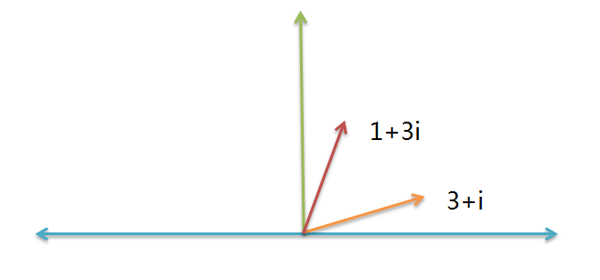
比如，物理学需要计算"力的合成"。假定一个力是 3 + i ，另一个力是 1 + 3i ，请问它们的合成力是多少？

了解本专栏 订阅专栏 解锁全文
重心，形心，质心 形心质心公式之一 形心质心公式之二​ 转换 ​​ 应用：举例：D:是圆；
ZJQ的博客
12-16 10万+
2、形心：物体的几何中心。(只与物体的几何形状和尺寸有关，与组成该物体的物质无关)。一般情况下重心和形心是不重合的，只有物体是由同一种均质材料构成时，重心和形心才重合。1、重心：物体的重力的合力作用点称为物体的重心。(与组成该物体的物质有关)3、质量中心简称质心，指物质系统上被认为质量集中于此的一个假想点。
行列式运算法则 矩阵的运算及其运算规则:
热门推荐
ZJQ的博客
10-29 8万+
1、三角形行列式的值，等于对角线元素的乘积。计算时，一般需要多次运算来把行列式转换为上三角型或下三角型 2、交换行列式中的两行（列），行列式变号（交换） 3、行列式中某行（列）的公因子，可以提出放到行列式之外。（倍乘）（注：矩阵是全部元素都乘，都提取） 4、行列式的某行乘以a，加到另外一行，行列式不变，常用于消去某些元素。（倍加） 5、若行列式中，两行（列）完全一样，则行列式为0；可以推论，如果两...
傅立叶变换
带着梦想飞
03-25 2130
Transformée de Fourier有多种中文译名，常见的有“傅里叶变换”、“傅立叶变换”、“付立叶变换”、“富里叶变换”、“富里哀变换”等等。为方便起见，本文统一写作“傅里叶变换”。应用傅里叶变换在物理学、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用（例如在信号处理中，傅里叶变换的典型用途是将信号分解成幅值分量和频率分量）。概要介
虚数i的理解
ZWEI_ccc的博客
07-07 377
引入了复数i，乘一个i表示旋转90度，乘两个i表示旋转180度，所以 i*i=−1
传统经典CV算法_拉普拉斯算子详解
欢迎大家关注我
10-04 1万+
拉普拉斯算子是一个二阶算子，比起一阶微分算子，二阶微分算子的边缘定位能力更强，锐化效果更好。 使用二阶微分算子的基本方法是定义一种二阶微分的离散形式，然后根据这个形式生成一个滤波模版，与图像进行卷积。 滤波器分各向同性滤波器和各向异性滤波器。各向同性滤波器与图像进行卷积时，图像旋转后响应不变，说明滤波器模版自身是对称的。如果是各向异性滤波器，当原图旋转90度时，原图某一点能检测出细节（突变）的，但是现在却检测不出来了，这说明滤波器不是对称的。由于拉普拉斯算子是最简单的各向同性微分算子，它具有旋转不变形。 对
傅里叶变换--图说
weixin_41469272的博客
03-09 6249
傅里叶 傅里叶变换将时域函数转换到频域上，可以用来解决实际的工程问题，如在音频特征的提取处理，图像特征的提取处理，另外也可以用来解决实际时域数学计算的困难性，如简化求解微分方程。 傅里叶级数 首先我们来讨论傅里叶级数， 任何周期函数，都可以看作是不同振幅，不同相位正弦波的叠加。如下图所示。 第一幅图是一个郁闷的正弦波cos（x） 第二幅图是2个卖萌的正弦波的叠加cos(x)+a.cos(3x) ...
复变函数：傅里叶变换
kking_edc的博客
11-02 5217
傅里叶级数针对周期函数，为了可以处理非周期函数，需要傅里叶变换。关于傅里叶级数的内容参见傅里叶级数 1 傅里叶级数 1.1 傅里叶级数是向量 从代数上看，傅里叶级数就是通过三角函数和常数项来叠加逼近周期为T的函数f(x)f(x)f(x)： 这一过过程，实际上是把f(x)f(x)f(x)当作了如下基的向量： 那么上面的式子就可以解读为： 以一个例子来说明，比如一个T=2πT=2\piT=2π的方波f(x)f(x)f(x)，可以粗略的写作f(x)≈1+4πsin(x)f(x)\approx1+{4\ove
傅里叶变换复数形式的实部代表什么_从 傅里叶变换 到拉普拉斯变换
weixin_39545269的博客
12-30 813
炫云：拉普拉斯变换的性质 炫云：傅里叶变换的全面理解，非常棒​zhuanlan.zhihu.com1、傅里叶变换(FT) 的优点和不足优点： 1、避免微分方程求解和卷积计算，简化了系统响应求解过程； 2、物理意义明确。如：谐波、频响、带宽等。不足： 1、只能处理满足收敛条件的信号，对某些不满足条件的信号必须引入奇异函数解决，不方便； 2、必须计算广义积分： ，有时计算比较困难； 3、只能求系统的...
为什么有了傅里叶变换我们还需要拉普拉斯变换？
weixin_43354598的博客
11-13 1621
傅里叶变换用于分析信号的频率成分，将时间域信号转化为频率域表示。 拉普拉斯变换是一种更广义的积分变换，通常用于分析动态系统。 本文对它们进行了介绍，并给出了为什么有了强大的傅里叶变换还需要拉普拉斯变换。
傅立叶变换和拉普拉斯变换的理解
最新发布
weixin_43233653的博客
04-30 923
本文系统介绍了信号与系统分析中的核心数学工具。首先阐述了复数基础及其几何意义，重点讲解了欧拉公式连接指数与三角函数的桥梁作用。随后详细解析了傅里叶级数分解周期信号的原理，并扩展到傅里叶变换进行非周期信号的频谱分析。文章进一步引入拉普拉斯变换处理不稳定系统，解释其与傅里叶变换的关系。最后深入探讨传递函数建模和零极点分析法，阐明极点位置对系统稳定性（实部符号）和动态特性（虚部决定振荡）的决定性作用。全文通过严谨的数学推导和直观的物理解释，构建了从时域到频域、从稳定到不稳定系统的完整分析框架。
【复变函数笔记】傅里叶变换和拉普拉斯变换
qaqwqaqwq的博客
06-06 6664
傅里叶积分定理若ftf(t)ft在−∞∞−∞∞上满足下列条件：(1)ftf(t)ft在任一有限区间上满足狄利克雷条件（连续或只有有限个第一类间断点；只有有限个极值点）；(2)ftf(t)ft在无限区间−∞∞−∞∞上绝对可积（即积分∫−∞∞∣ft∣dt∫−∞∞​∣ft∣dt收敛），则有ft12π∫−∞∞∫−∞∞fτe−iωτdτeiωtdωft2π。
傅里叶变换，拉普拉斯变换和Z变换的意义
08-03
"傅里叶变换、拉普拉斯变换和Z变换的意义" 傅里叶变换是解决问题的方法，一种工具，一种看待问题的角度。它将一个信号的时域表示形式映射到一个频域表示形式，从而将信号分解成幅值分量和频率分量。傅里叶变换在...
傅里叶、拉普拉斯变换公式
分享各种学习心得和遇到的问题
06-23 1382
【衰减因子：e 的 - xita t 次方】这些公式用于分析和处理信号在不同域中的表现。
傅里叶变换 与 拉普拉斯变换（更广泛）
分享各种学习心得和遇到的问题
06-19 1340
这个公式的含义是：对于给定的频率 (\omega)，将时域信号 ( x(t) ) 乘以 ( e^{-j\omega t} ) 并对整个时间范围内进行积分，得到该频率成分的复数值 ( X(j\omega) )。这个复数值表示信号在该频率下的幅度和相位。这个公式的含义是：对于给定的复数 ( s )，将时域信号 ( x(t) ) 乘以 ( e^{-st} ) 并对整个时间范围内积分，得到复频域信号 ( X(s) )。拉普拉斯变换将时域信号 ( x(t) ) 转换为复频域信号 ( X(s) )。
拉普拉斯变换、傅里叶变换、Z变换公式
分享各种学习心得和遇到的问题
06-25 1936
定义： L{f(t)}=F(s)=∫0∞f(t)e−st dt\mathcal{L}\{f(t)\} = F(s) = \int_{0}^{\infty} f(t)e^{-st} \, dtL{f(t)}=F(s)=∫0∞​f(t)e−stdt 其中，s 是复数变量，s=σ+jωs = \sigma + j\omegas=σ+jω逆变换： L−1{F(s)}=f(t)=12πj∫σ−j∞σ+j∞F(s)est ds\mathcal{L}^{-1}\{F(s)\} = f(t) = \frac{1}{2\pi
绕x,y轴旋转曲面面积公式推导
ZJQ的博客
12-17 8万+
绕x轴旋转曲面面积公式：其中，y1(x)和y2(x)分别是旋转曲面的上下边界函数。绕y轴旋转曲面面积公式：其中，x1(y)和x2(y)分别是旋转曲面的上下边界函数。
向量组a可由向量组b线性表示什么意思
ZJQ的博客
10-22 3万+
重要性质 1、向量组B=(β1，β2，……，βm)能由向量组A=(α1，α2，……，αm)线性表示的充要条件是： 矩阵A=(α1，α2，……，αm)的秩=矩阵(α1，α2，……，αm，B)的秩。 2、向量组B能由向量组A线性表示，则向量组B的秩不大于向量A的秩。反之不一定成立。 3、一个向量可由向量组中其余向量线性表示，前提是这个向量组线性相关。线性相关的向量组中并不是任一向量都可由其余向...
矩阵的等价，相似，合同，正定判定和关系
ZJQ的博客
11-02 3万+
矩阵等价（秩等） 定义：对同型矩阵A、B，存在可逆阵P和Q，使得B=PAQB=PAQ 充要条件：A和B的秩相等 补充： 向量组AB等价（r(A)=r(B)=r(AB)；可以相互线形表示；极大线形无关组同） 转置理解：就是关于x=y对称的同体，二维是关于y=x 对称的平面图形，三维是关于f(x,y)=x-y 对称的 立方体或者图形，以此类推 |A转置|=|A|:可是用行列式值对的意义理解：...
A的转置乘以A的秩 等于 A乘以A的转置的秩，也等于A的秩； r(a+b)＜=r(a)+r(b)：极大线性无关组证明；
ZJQ的博客
11-26 2万+
前提条件：实矩阵。 R（AB）<=MIN(R(A),R(B)) A的转置乘以A的秩 等于 A乘以A的转置的秩，也等于A的秩; A是 m*n 矩阵。可以使用：R（AB）<=MIN(R(A),R(B))；结合行秩，列秩，秩，三秩相等； 例子： 还可以使用同解同秩结论： 1、Ax=0 肯定是 A'Ax=0 的解,好理解. 2、A'Ax=0 → x'A'A...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

ZhangJiQun&MXP

等到80岁回首依旧年轻

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值