汉诺塔
 |
汉诺塔问题是一个经典的问题。汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着N片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移动一个圆盘。问应该如何操作?
试想一下,如果我们要将最大的圆盘移动到最右边的柱子上。我们需要把除此圆盘的其他圆盘先移动到中间的柱子上。因此这个问题就变成了如何将 N-1 个圆盘移动到中间的柱子上。很容易我们就想到了递归的方法。
将 N 个圆盘从左边柱子移动到右边柱子:
- [递归的]将 N-1 个圆盘从左边柱子移动到中间柱子。
- 将最大的圆盘从左边柱子移动到右边柱子。
- [递归的]将 N-1 个圆盘从中间柱子移动到右边柱子。
算法实现
def hanoi(height, left='left', right='right', middle='middle'):if height:hanoi(height - 1, left, middle, right)print(left, '=>', right)hanoi(height - 1, middle, right, left)hanoi(3) |
计数 1 的位数
当你写下一个正整数的二进制数形式时,有没有想要探究一下这个二进制数里有多少位数为1呢?
例如:99 = 0b1100011
一个明显的解法即是去获得一个单位掩码,遍历这个二进制数 X & (1 << k) 并返回非零的结果,这种方式将0的位数与1的位数都计算在内。
有没有更好的方式可以只计数1的位数而完全忽略0的位数呢?你可以有自己更多美妙的想法,但是我们并不需要它们。
算法实现
| def count_of_1bits(value): n = 0 while value: value &= value - 1 n += 1 return n |
埃拉托色尼筛选法
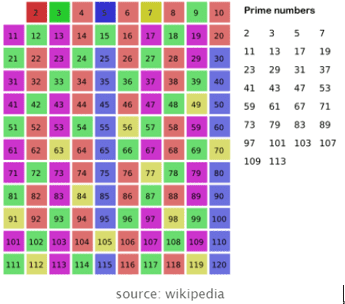 |
埃拉托色尼筛选法是一个很漂亮的示例算法。
在 i7 CPU(单线程)处理器下它可以在1s之内生成10^9以内的所有素数,因此,当这种筛选算法被应用的时候,它的速度是非常惊人的。
而我用了最基础的版本(未进行分割),仅仅只是删除了在数组中的偶数。
算法实现
| import numpy as np def eratosthenes(n): n = (n + 1) >> 1 p = np.ones(n, dtype=np.int8) i, j = 1, 3 while i < n: if p[i]: p[j * j >> 1::j] = 0 i, j = i + 1, j + 2 return p.sum() |
蒙特卡洛法
蒙特卡洛方法又称统计模拟法,随机抽样技术,是一种随机模拟方法,以概率和统计理论方法为基础的一种计算方法。是使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系,用电子计算机实现统计模拟或抽样,以获得问题的近似解。为象征性地表明这一方法的概率统计特征,故借用赌城蒙特卡罗命名。
早在17世纪,人么就知道用事件发生的“频率”来决定事件的“概率”。这也是蒙特卡洛法的基本思想。当样本数量足够大时,我们可以用频率去估计概率。这也是求圆周率π的常用方法。
求圆周率π
在只有一个随机数生成器的情况下如何估计π的大小?
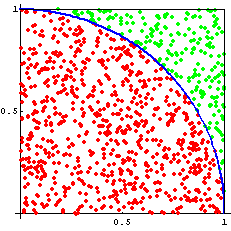 |
当我们在(-1, 1)的范围内随机选择一个坐标(x, y)时,每个坐标点被选中的概率相等。则坐标落在直径为1的正方形中的圆的概率为:
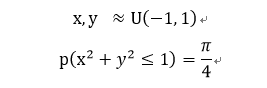 |
由切比雪夫不等式可知,在生成大量随机点的前提下我们能得到尽可能接近圆周率的值。
算法实现
|
import numpy as np def pi(n, batch=1000): t = 0 for i in range(n // batch): ### 随机获取坐标 p = np.random.rand(batch, 2) ### 计算坐标平方和 p = (p * p).sum(axis=1) ### 平方和小于1的即为落在圆中的点 t += (p <= 1).sum() return 4 * t / n |
测试
|
firstPi = pi(10 ** 3) secondPi = pi(10 ** 6) thirdPi = pi(10 ** 8) print(firstPi) print(secondPi) print(thirdPi) |










 本文深入探讨了汉诺塔问题的递归解法,介绍了快速计数二进制中1的位数的技巧,展示了埃拉托色尼筛选法高效生成素数的威力,并利用蒙特卡洛法估算圆周率π,提供了丰富的算法实现代码。
本文深入探讨了汉诺塔问题的递归解法,介绍了快速计数二进制中1的位数的技巧,展示了埃拉托色尼筛选法高效生成素数的威力,并利用蒙特卡洛法估算圆周率π,提供了丰富的算法实现代码。
















 6786
6786

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








