park把clark输出的lA IB进行带角度正交分解承IQ ID,因为有角度,所以可化为360度转动的矢量
反park就是把带角度的正交的两个矢量转化为IA IB两个轴,IA IB只有大小好方向,角度固定不带可动

Clark出来的IA IB
坐标轴受力分析
IB为 OB
IA为OH
IB和IA的正交合力是OC,OHCB是矩形
OC分解为带角度的正交分力:这里的一个角度确定一个正交2分力,也就是一个固定角度只有一个固定的正交2分力;
所以两个Z是相等的值;四边形OGCF是矩形;
做直线AB垂直于OA的直线,BD垂直于GC,作为辅助计算;此时存在四边形AGDB是矩形;
做直线EH垂直于OF的直线,HG垂直于CJ,作为辅助计算,此时存在HJFE是矩形
因为CG平行OF,所以角GCO等于角COF
OB平行CH,所以角BOC等于角OCH
因为90=角BCH
且90=角BOH
所以角BCD等于角FOH等于Z
同理求证角HCJ等于Z
因为OH等于BC=IA
所以BD=sinz*BC =sinz *IA
所以OB等于HC=IB
所以HJ=sinz*HC=sinz*IB
因为四边形AGDB是矩形,HJFE是矩形
所以AG=sinz *IA
所以EF=sinz*IB
由图可知
OE=cosz*IA
OA=cosz*IB
因为矢量的方向;
ID=cosz*IA+sinz*IB
IQ= -sinz *IA+cosz*IB

由
线性矩阵H=K*L K1为K的逆矩阵;
L=K1*H
所以求出
的逆矩阵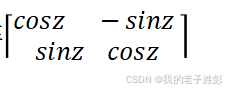

























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








