分析:
OEIS大法好哇。。。
暴力打表然后去OEIS上面搜一下,
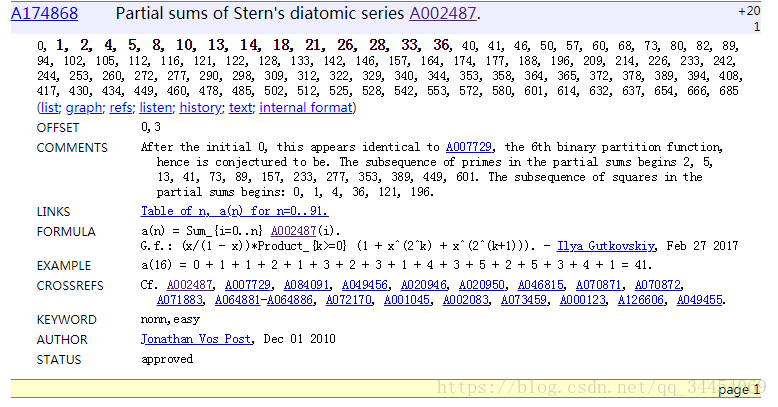
get…
但似乎没有给公式啊
嗯。。再看看
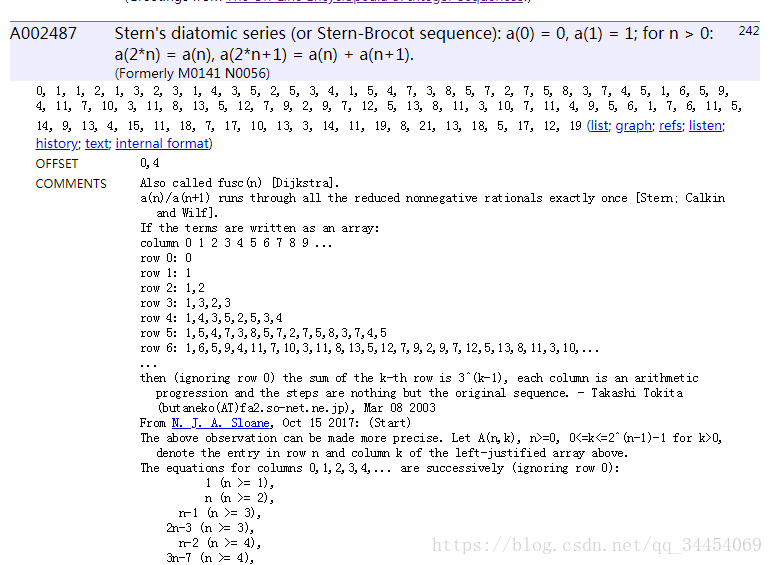
似乎是这玩意的前缀和啊,这玩意给了个递推公式。。。
然后用数学老师讲的方法:
a1=a1a1=a1
a2=a1a2=a1
a3=a1+a2a3=a1+a2
a4= a2a4= a2
a5= a2+a3a5= a2+a3
a6= a3a6= a3
a7= a3+a4a7= a3+a4
然后就能很轻松地发现:
S2∗n=3×Sn−anS2∗n=3×Sn−an
S2∗n+1=3×Sn+an+1S2∗n+1=3×Sn+an+1
然后就可以求啦。。。先预处理出a1到a1000000a1到a1000000,然后就可以O(logn)求了。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#define SF scanf
#define PF printf
#define MAXN 1000010
#define INF 0x3FFFFFFF
#define MOD 1000000007
using namespace std;
typedef long long ll;
ll n,n1;
ll a[MAXN];
map<ll,ll> mp;
ll p(ll x){
if(mp.count(x))
return mp[x];
if(x<=1000000)
return a[x];
if(x==1)
return 1;
if(x%2ll==1ll)
mp[x]=(p(x/2ll)+p(x/2ll+1ll))%MOD;
else
mp[x]=p(x/2ll);
return mp[x];
}
ll que(ll x){
if(x==1)
return 1;
if(x%2ll==1ll)
return (que(x/2ll)*3ll+p(x/2ll+1ll))%MOD;
else
return (que(x/2ll)*3ll-p(x/2ll)+MOD)%MOD;
}
void prepare(){
a[1]=1;
for(int i=1;i<=1000000;i++){
if(i%2==1)
a[i]=(a[i/2]+a[i/2+1])%MOD;
else
a[i]=a[i/2];
}
}
int main(){
prepare();
SF("%lld",&n1);
n1++;
PF("%lld\n",que(n1));
} 









 本文介绍了一种使用OEIS在线数列百科全书来快速查找数列规律的方法,并给出了具体的递推公式及实现代码。通过预处理大量数据点,可以实现O(logn)的时间复杂度求解。
本文介绍了一种使用OEIS在线数列百科全书来快速查找数列规律的方法,并给出了具体的递推公式及实现代码。通过预处理大量数据点,可以实现O(logn)的时间复杂度求解。
















 612
612

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








