本文介绍了A星算法原理及其在数码问题中的应用，通过启发式函数指导搜索过程，实现从初始状态到目标状态的最优路径寻找。
A星算法及数码问题实践
- 算法原理
- 算法伪码
- 解决数码问题
- 算法可视化演示
算法原理
A星算法基于或图通用搜索算法，所谓或图通用搜索，即在或图对应的背景为搜索扩展时，可在若干分支中选择其中之一（“或“的意思）。本质上就是启发式搜索，它是围绕着启发式函数展开搜索的。图搜索算法维护两个存放结点的表：Open表用于存放已经生成，且已用启发式函数做过估计或评价，但未产生他们的后继结点的那些结点，也称考察结点；Closed表用于存放已经生成，且已考察过的结点。
在或图通用搜索算法中，记S0为起始点而Sg为终点，将启发式函数的形式定义为f(n) = g(n) + h(n)，其中g(n)表示从S0到n点的实际搜索费用，n为当前节点，搜索已达到n点，所以g(n)可以计算出。h(n)表示从n到Sg的估计程度，它仅仅是一个估计值。根据f(n) = g(n) + h(n)启发式函数展开搜素的就是A算法，注意此时还不是A星算法，每一次搜索计算它的启发式函数值，从当前获取的搜索集中取一个启发式函数最优的作为下一个状态，不断迭代。
A星算法由A算法进一步扩展而来，令h*(n)表示n到Sg的实际最小费用，那么令启发式函数f(n) = g(n) + h(n)中，h(n) <= h*(n)恒成立，那么根据该启发函数展开搜索的算法就是A星算法。即A星算法是由A算法进一步约束而来的。A星算法具有良好的性质，可采纳性、信息性、单调性，如果问题有解，则A星算法一定能够找到最优解。
算法伪码
设S0为初始状态，Sg为目标状态：
（1）Open = {S0}。
（2）Closed = { }。
（3）如果Open = { }，失败退出。
（4）在Open表上取出f(n)值最小的结点n，n放到Closed表中，即f(n) = g(n) + h(n)中，h(n) <= h*(n)
（5）若n为Sg，则成功退出。
（6）产生n的一切后继，将后继中不是n的前驱结点的一切点构成解M。
（7）对集合M中的元素P，分别作两类处理：若P不在图G中，则对P进行估计加入Open表，记入G和Tree；若P已经在图G中，则决定更改Tree中P到n的指针，并且更改P的子节点n的指针和费用。
（8）转第（3）步。
解决数码问题
数码问题背景
个3*3的棋盘上摆放着1-8八个棋子，留下一个空位，与空位相邻的棋子可以移动到空位中。八数码要求以最少的移动次数，将一个给定的初始状态变成目标状态，并给出移动棋子的步骤。除了八数码问题，还有它的扩展九数码。
拟定算法
(1)、数据结构：用一个整数表示一个八数码状态，如012345678，表示从右下角到左上角的迂回序列。open表的数据结构表示，考虑对open表的操作，每次需要得到所有待扩展结点中 f 值最小的那个结点，用堆进行实现。判断一个解是否出现过，用set记录已经出现的解。
(2)、初始化，分别输入初始序列和目标序列。
(3)、判断是否能够从初始序列移动到目标序列，计算节点的逆序对数。将初始序列的逆序对数与目标序列的逆序对数比较，若不能则停止，否则下一步。
(4)、初始化Open表，将初始节点放入其中。Close表为空。下面开始正式的解空间查找过程，采用的是广度优先遍历算法。
(5)、从Open表取出头节点，因为Open是heap结构，头部的就是最优节点。将其加到Close表，并Open表删除。判断这个节点是否是目标节点，是则立即结束程序。
(6)、根据当前的节点向它的四个方向扩展子节点，注意边界判断。获取它的子节点，在这里要在进行一次有效判断，判断该子节点能够移动到目标节点，不能则丢弃。
(7)、重复上面的步骤5和6。
对于启发式函数f(n) = g(n) + h(n)中，h(n) <= h*(n)，令g(n)表示广度搜索的深度，h(n)估计放错位置的数字个数或当前位置与目标状态的欧拉距离，可以看出g(n)还远未考虑从放错位置到正确位置要移动的困难程度，符合A星算法的条件。
编程实现
解的状态表示:
struct node//每次解的状态表示
{
/*棋盘 8 7 6
5 4 3
2 1 0
用整数012345678表示
*/
int state;//棋盘状态表示
int blank;//空格位置
int g;//g(n)
int h;//h(n)
int pre;//前驱，用于获取最终路径
node(){
state = blank = g = h = pre = 0;
}
};算法类:
class EightNumbers{
private:
node head;
node open[MAXSTEPS]; //open表
pair<int, int> closed[MAXSTEPS];//close表
vector<int> path;//结果的路径
set<int>states;//状态空间，用于判断当前解是否已经生成过
int steps;
int Target;//目标状态
int Current;//当前状态
inline bool CouldMove(int a,int b){//边界判断
return (a >= 0 && a < 3 && b >= 0 && b < 3);
}
inline bool CouldSolve(int current,int target){//判断能够达到目标状态
int targetNum = GetNixuNum(target);
int currentNum = GetNixuNum(current);//计算逆序对
return ((currentNum&1)&&(targetNum&1))||
(!(currentNum&1)&&!(targetNum&1));
}
inline int GetZeroLocation(int target){//获取0的位置
int ret = 0;
while(target != 0){
if(target%10 == 0)break;
++ ret;
target /= 10;
}
return ret;
}
void GetPath(int index);
public:
EightNumbers(int cur,int tar){
Current = cur;
Target = tar;
steps = 0;
}
~EightNumbers(){}
void SetInit(int current,int target);//初始化
int Calculate(int current,int target);//启发式函数1，估计错放位置到目标位置欧拉距离
int Calculate1(int current,int target);//启发式函数2，估计错放棋子的个数
int GetNixuNum(int state);//计算逆序
bool aStarAlgorithm();//A星算法
void ShowPath();//打印路径
void GetSolution();//获取结果
};启发式函数的两种计算:
int EightNumbers::Calculate(int current, int target)
{
int c[9], t[9];
int ret = 0;
//提取每个棋子的数字
for(int x = 0;x < 9; ++ x){
c[current % 10] = t[target % 10] = x;
current /= 10;
target /= 10;
}
for(int x = 1;x < 9;++ x)//计算当前状态到目标状态的欧拉距离
ret += abs(c[x] / 3 - t[x] / 3) + abs(c[x] % 3 - t[x] % 3);
return ret;
}
int EightNumbers::Calculate1(int current,int target)
{
int c[9], t[9];
int ret = 0;
for(int x = 0;x < 9; ++ x){
c[current % 10] = t[target % 10] = x;
current /= 10;
target /= 10;
}
for(int x = 1;x < 9;++ x){//放错棋子的个数
if(abs(c[x]/3 - t[x]/3)+abs(c[x]%3-t[x]%3) > 0)++ ret;
}
return ret;
}算法演算：
bool EightNumbers::aStarAlgorithm(){
int NextNode;
pair<int,int>start,targets;//起始、目标状态
//first记录棋局状态,second记录空格位置
start.first = Current;start.second = GetZeroLocation(Current);
targets.first = Target;targets.second = GetZeroLocation(Target);
if(!CouldSolve(start.first,targets.first))//判断能够达到目标状态
return false;
open[0].state = start.first;//加入open表
open[0].h = Calculate1(start.first,targets.first);
open[0].blank = start.second;
open[0].pre = -1;
open[0].g = 0;
int index = 0;
states.insert(start.first);//记录已扩展的解
int nums = 1;
for(;nums > 0;++ index){
//cout << "1" << endl;
assert(index < MAXSTEPS);
head = open[0];//从Open表去除头部结点，因为open表为最小heap结构
//Get the smallest f(n) to closed table
closed[index].first = open[0].state;
closed[index].second = open[0].pre;
pop_heap(open,open+nums,cmp());
-- nums;
//already got the solution
if(head.state == targets.first){
GetPath(index);
break;
}
int x = head.blank / 3;
int y = head.blank % 3;
//expand the sub nodes
for(int i = 0;i < 4;i ++){
int nx = x + xtran[i];
int ny = y + ytran[i];
if(!CouldMove(nx,ny))//不能达到目标状态丢弃
continue;
int na = head.blank;
int nb = 3*nx + ny;
//the next sub node
NextNode = head.state +
((head.state % p[na+1]) / p[na] -
(head.state % p[nb + 1]) / p[nb]) *p[nb]
+
((head.state % p[nb + 1]) / p[nb] -
(head.state % p[na + 1]) / p[na]) *p[na];
if(!CouldSolve(NextNode,targets.first))continue;
if(states.find(NextNode) != states.end())continue;
states.insert(NextNode);
open[nums].pre = index;
open[nums].blank = nb;
open[nums].state = NextNode;
open[nums].h = Calculate1(NextNode,targets.first);
open[nums].g = head.g + 1;
++ nums;
push_heap(open,open+nums,cmp());
}
}
cout << "states->" << states.size() << endl;
states.clear();
steps = 0;
return nums > 0;
}算法可视化演示
八数码问题:
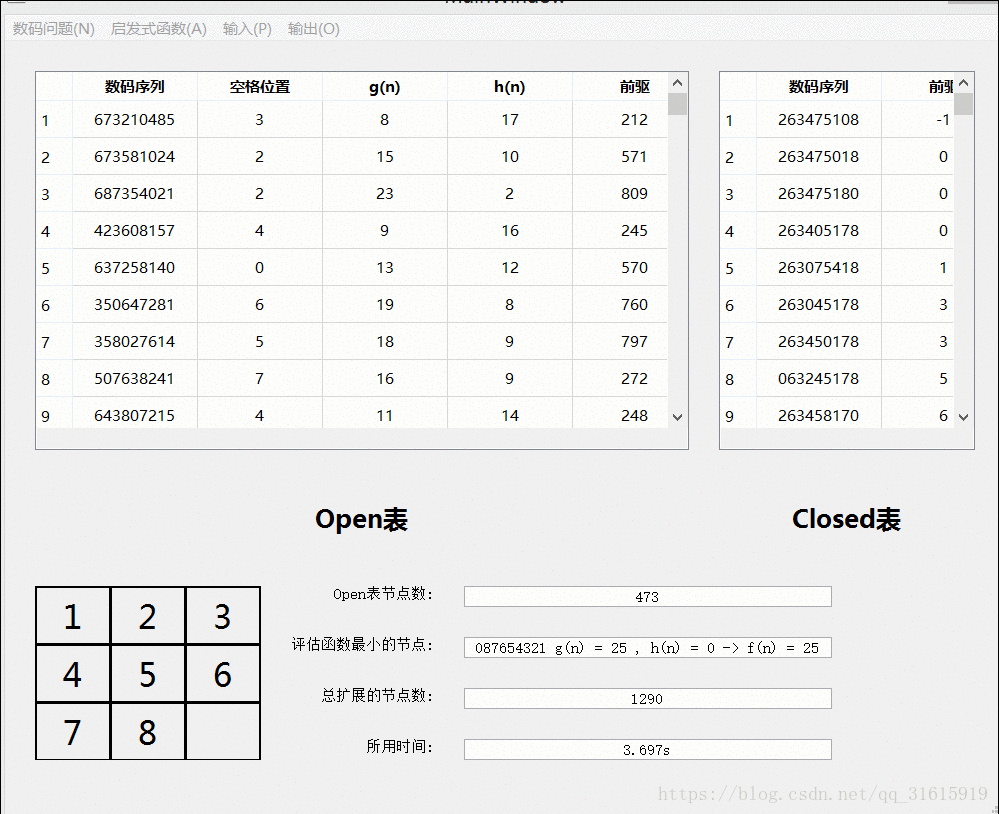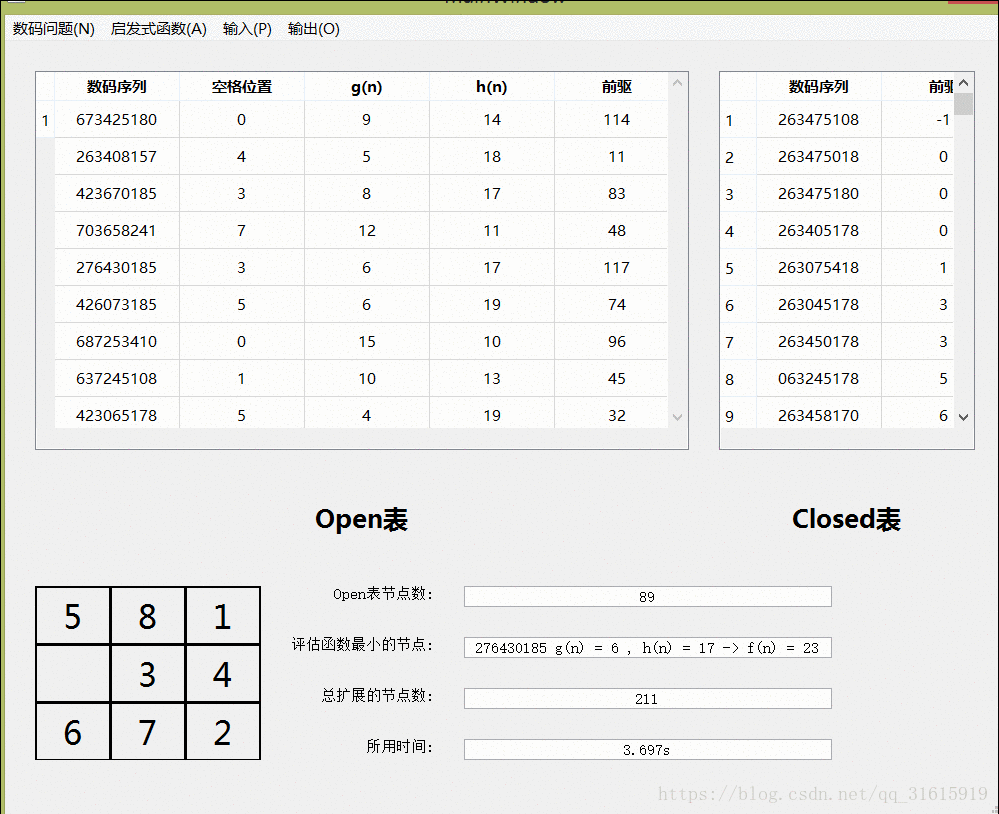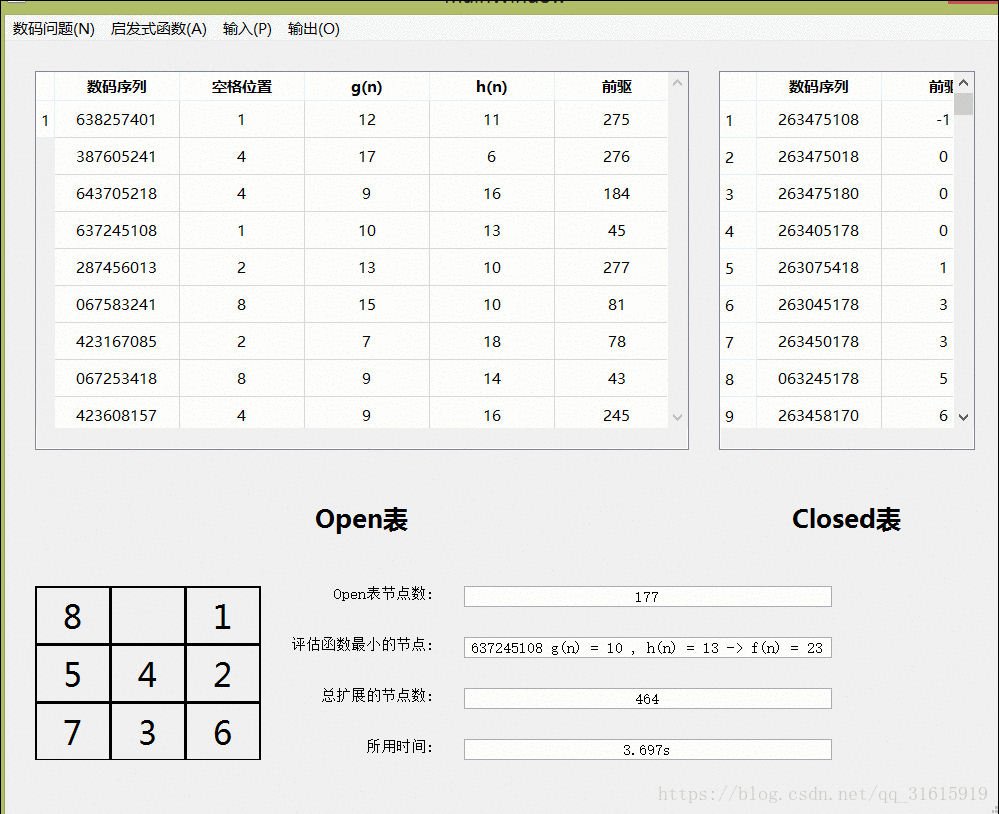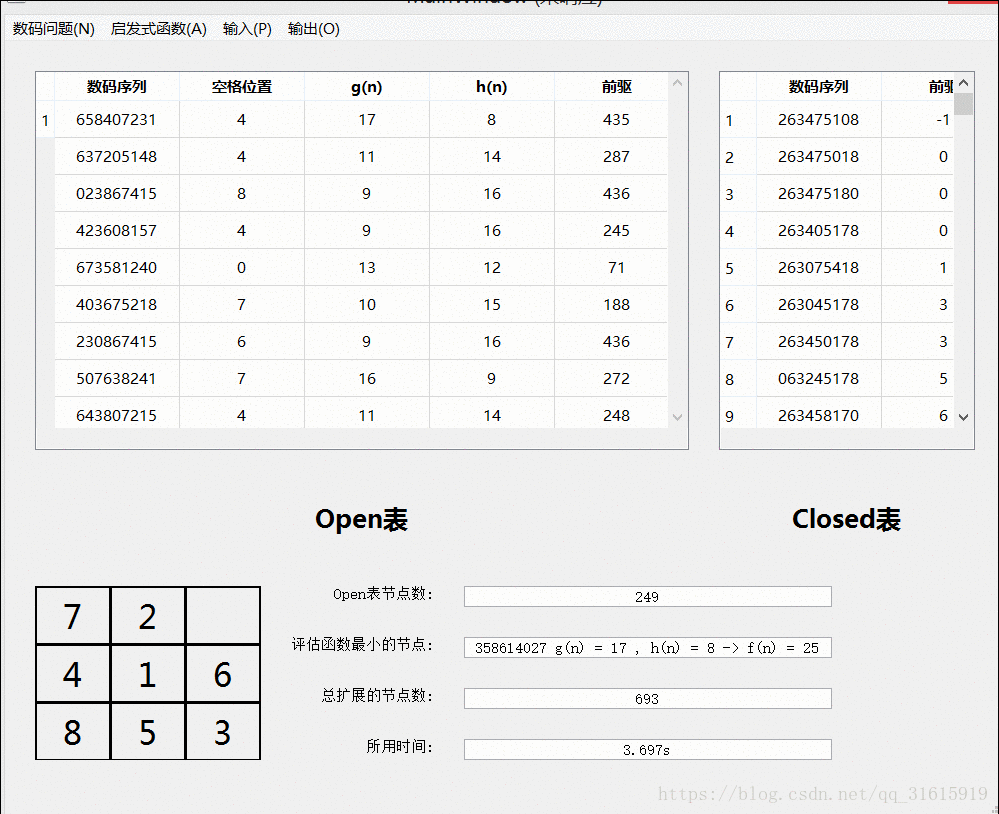
九数码问题：九数码的大部分框架都沿用了八数码的，他们的不同之处在于广度优先搜索时，扩展的子节点的方式不同。八数码仅仅考虑了空格的移动，而九数码考虑的是每一个数字的移动，这样每次扩展的子节点数大大增加了，这时求解的速度也会增加。另外一点需要注意的是，九数码不再需要判断当前解是否有效，不同于八数码，九数码的每一个子节点都能达到目标节点状态，这是规则的不同造成的差异，如此一来，九数码也省去了判断的步骤。
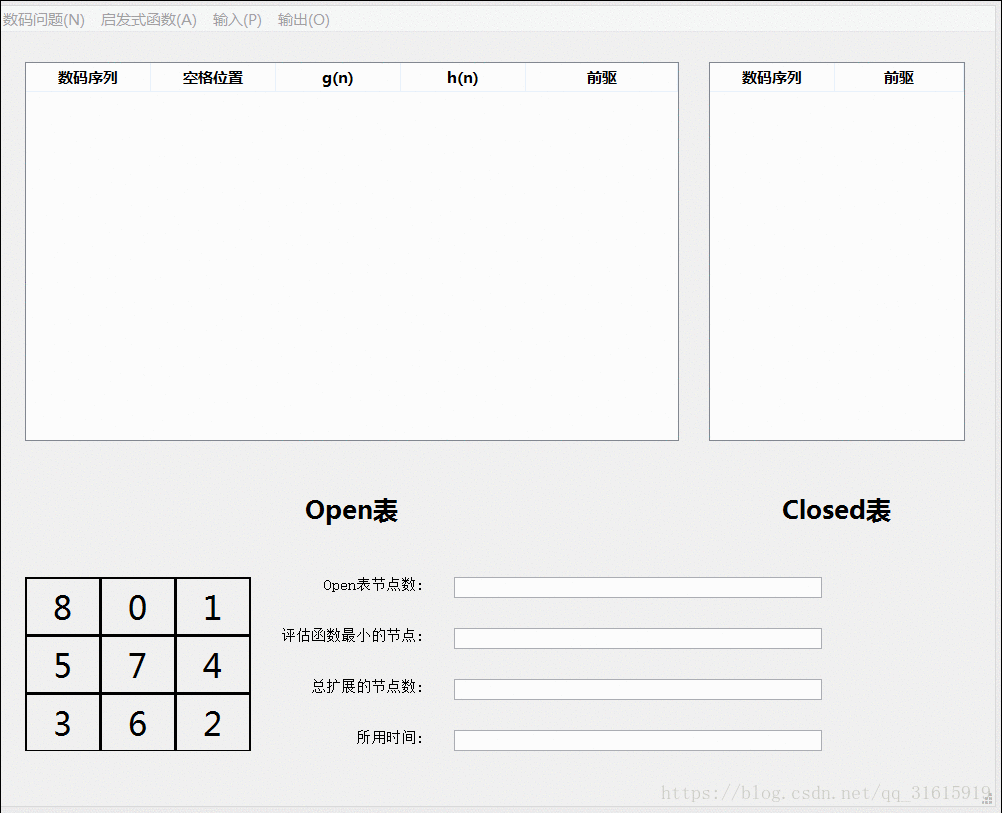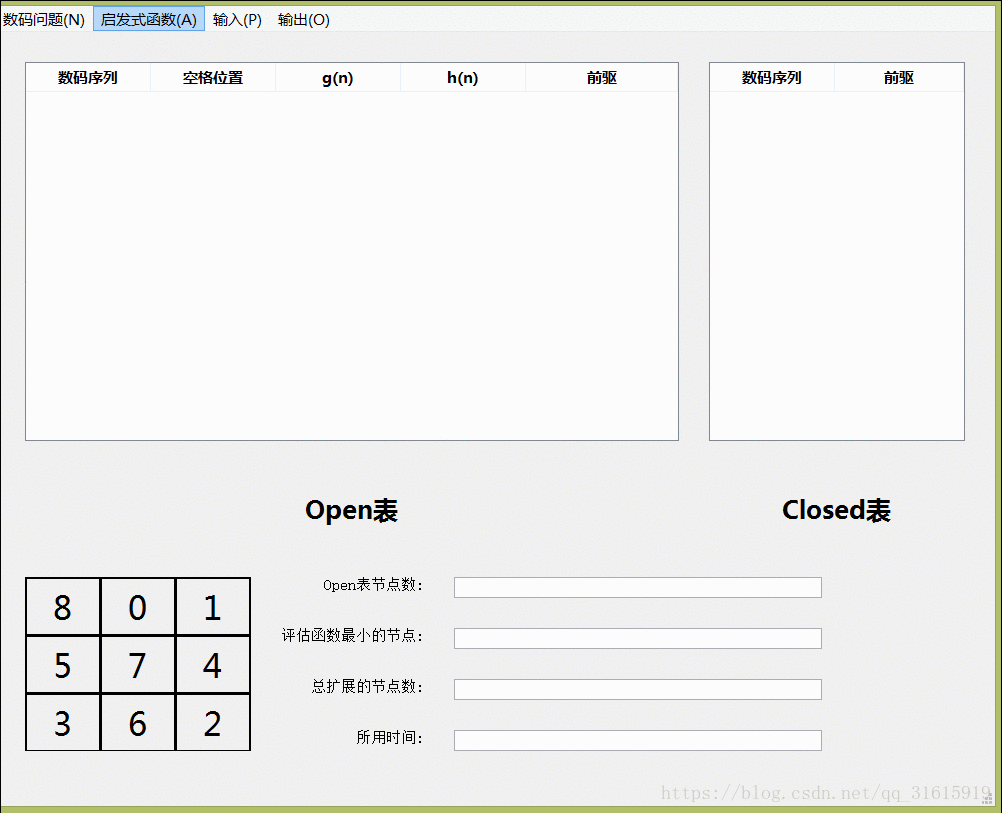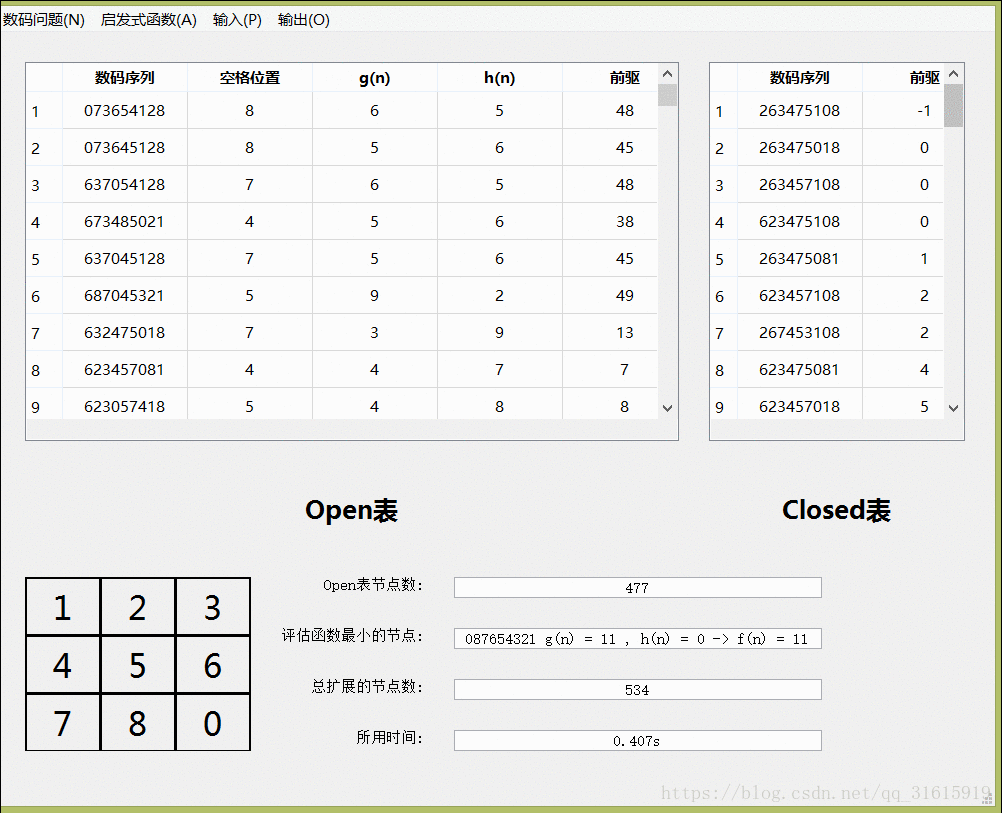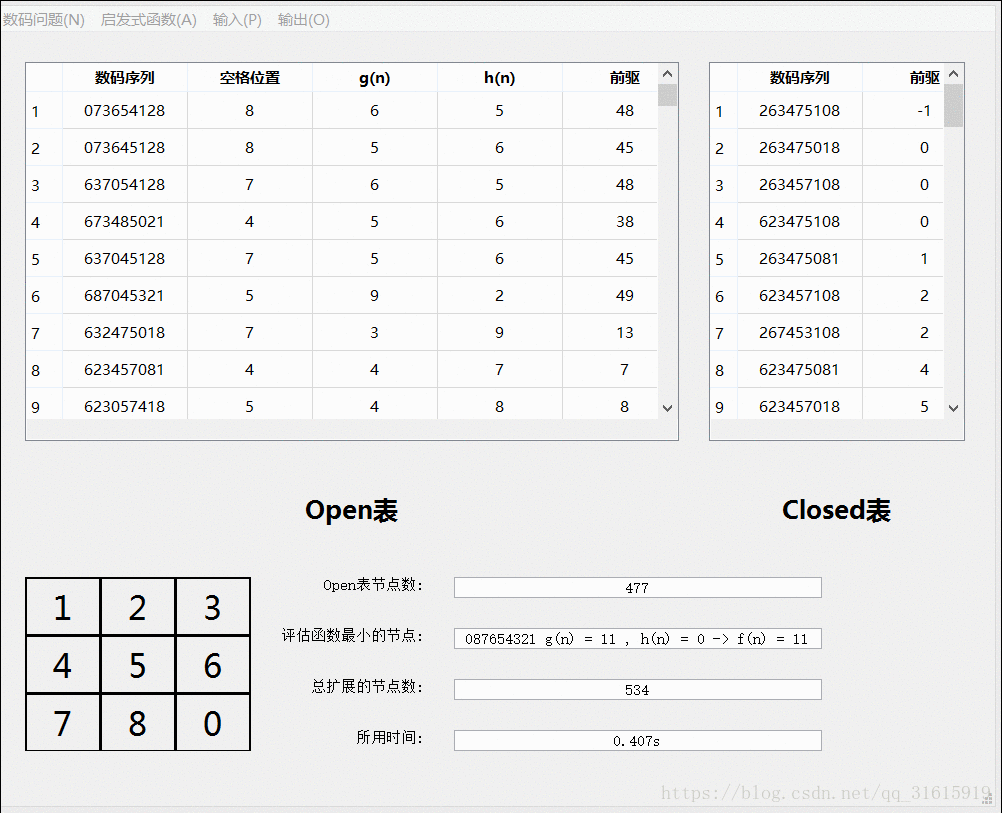
可以看到九数码的速度非常快，从初始到目标的路径演示：
核心源码和测试数据下载（无GUI)：https://github.com/ZeusYang/AILearning
参考资料：《人工智能基础教程（第二版》作者：朱福喜
扫一扫
699
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
