对支持向量机的数学推导（个人理解的内容）

最新推荐文章于 2025-04-22 23:13:19 发布

逃课去学习:)

最新推荐文章于 2025-04-22 23:13:19 发布

阅读量663

点赞数 2

CC 4.0 BY-SA版权

分类专栏：机器学习文章标签：机器学习

本文链接：https://blog.youkuaiyun.com/qq_29978597/article/details/88753177

本文详细介绍了支持向量机（SVM）的数学推导，从核心思想、超平面的寻找、函数间隔与几何间隔的概念，到如何求解最优超平面的w和b，以及最大软间隔、非线性SVM的处理。通过拉格朗日对偶性、核函数和SMO算法，逐步解析SVM的实现过程，帮助读者深入理解这一重要的机器学习算法。

支持向量机可谓是机器学习道路上的第一个拦路虎，不仅证明复杂，而且很多入门资源也并不适合新手，本人足足花了半个多月的时间，才对整体的数学推导有了一些掌握，写个博客，加深记忆。文章有什么不好理解的请提交评论。

提前说明

下面的截的图里w（带T上标的）跟正文中的w都表示法向量。

1. 什么是支持向量机

支持向量机是机器学习领域的一种分类算法，通常用来解决二分类问题。

2. 核心思想

       以简单的二分类为例，传统的分类器，比如感知器、逻辑回归都是找一个超平面将正例与反例分开。支持向量机也是如此。
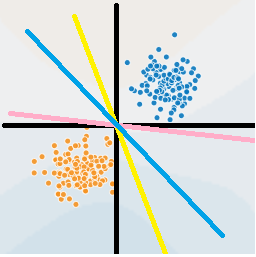
       但有一点不同，支持向量机除了能找到超平面分开正反例，还能保证该超平面是最好的分界面，如下图，
       下面三条线哪一条能最好地将正反例分开，显然是中间的蓝线，因为数据集的局限性和难以避免的噪声因素，训练集外的样本可能比图中的样本更靠近中间，中间的蓝线比其他两条线更难受此影响。
       因此，这也是支持向量机要解决的核心思想，找到最优的超平面来分割样本。
在这里插入图片描述

3. 如何找到这样的最优超平面

       首先，我们给出表示超平面的线性方程：
        wx+b=0。
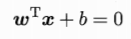
       （这里的w表示法向量，控制超平面的方向；b表示截距，控制超平面到原点的距离。）
       为了找到这样一个超平面，我们要让离他最近的样本点到超平面的距离尽可能地大。因此首先我们需要一个点到超平面的距离的表示方法。

函数间隔的定义

先给出函数间隔的定义，后面要用到。通常的，一个点距离超平面的远近可以表示分类预测的确信程度，在超平面wx+b=0确定的情况下，|wx+b|能相对表示样本点x到超平面的远近。而预测值wx+b的符号和真实标记y的符号是否一致表示分类是否正确，可用y(wx+b)表示分类的正确性和确信度，这就是函数间隔的概念。

       但函数间隔并不是一个确定的值，不能用来表示点到超平面的距离。比如把w和b放大到2倍，2*(wx+b)=0，还是原来那个超平面，但函数间隔|2*(wx+b)|却扩大了两倍。
       因此要引入几何间隔的公式，
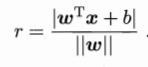
        在这里插入图片描述
       几何间隔的大小不会受到w和b缩放的影响，因为下方的||w||也会等比例缩放，跟上面的抵消了。