本文简要介绍了支持向量机的基本原理，包括超平面表示、点到超平面的距离以及如何确定最优间隔。在硬分类中，讨论了最大化间隔的目标函数和线性可分优化问题。此外，还提到了支持向量机处理线性不可分问题时采用的核函数技巧，如高斯核函数，使得低维数据能在高维空间进行有效分类。
超平面表示：g(x) = wx + b
空间中点到超平面的距离：M = |g(x)| / ||w||
间距越大，容错越强
分界面只是由边缘部分点的控制，与边缘部分的点相切的向量可以理解为支持向量
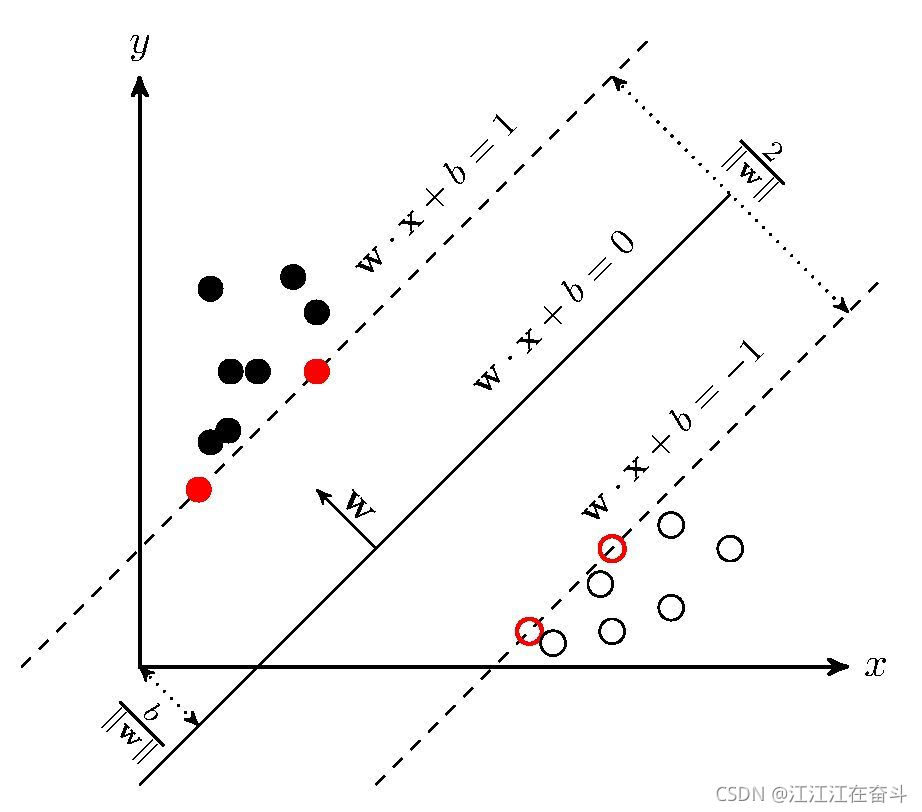
可以通过缩放w与b的值 使g(x) = 1，g(x) = -1
点到超平面距离：M = |g(x)| / ||w|| = 2 / ||w||
硬分类：
1.把样本分好，打标签 使 g(x) = 1，g(x) = -1
w·x + b ≥1， if yi = +1
w·x + b ≤1， if yi = -1；
上述 yi（w·x + b）-1 ≥ 0；
2. max M = 2 / ||w|| —— min 1/2 w' · w
3. 线性可分优化问题
目标函数：φ(x) = 1/2 w' · w
任意样本满足：yi（w·x + b）≥ 1；
软分类：
目标函数：φ(x) = 1/2 w' · w + ci
i ≥0
任意样本满足：yi（w·xi + b）-1 +
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
