分治法-最接近点对问题

背景：

计算机应用中经常采用点、圆等简单的几何对象表示物理实体，常需要了解其邻域中其他几何对象的信息

• 例如：在空中交通控制中，若将飞机作为空间中的一个点来处理，则具有最大碰撞危险的两架飞机所处的点对，就是这个空间中距离最接近的一对点。

这类问题是计算几何学中研究的基本问题之一。

我们着重考虑平面上的最接近点对问题。

最接近点对问题：

给定平面上的n个点，找出其中的一对点，使得在n个点组成的所有点对中，该点对的距离最小。

直观解法：

• 将每一个点与其他n-1个点的距离算出，找出最小距离。
• 时间复杂度：T(n)=n(n-1)/2+n=O(n2)，ps：求出n(n-1)/2个点对距离的时间+求出最短距离的时间

分治法：

• 分解：将n个点的集合分成大小近似相等的两个子集。
• 求解：递归地求解两个子集内部的最接近点对。
• 合并（关键问题）：从子空间内部最接近点对，和两个子空间之间的最接近点对中，选择最接近点对。

1、一维最接近点对问题

算法思路：

考虑将所给的n个点的集合S分成2个子集S1和S2，每个子集中约有n/2个点，然后在每个子集中递归地求其最接近的点对。

关键的问题是分治法中的合并步骤：

• 由S1和S2的最接近点对，还要求得原集合S中的最接近点对，因为S1和S2的最接近点对未必就是S的最接近点对。
• 如果这2个点分别在S1和S2中，则对于S1中任一点p，S2中最多只有n/2个点与它构成最接近点对的候选者。
• 仍需做n^2/4(n/2*n/2)次计算和比较才能确定S的最接近点对。
• 合并步骤耗时为O(n^2)，整个算法所需计算时间T(n)应满足:　T(n)=2T(n/2)+O(n^2)。
• 因此，问题出在合并步骤耗时太多。

用x轴上某个点m将S划分为2个子集S1和S2，使得S1={x∈S|x≤m}；S2={x∈S|x>m}。

因此，所有p∈S1和q∈S2有p<q，递归地在S1和S2上找出其最接近点对{p1,p2}和{q1,q2}，并设d=min{|p1-p2|,|q1-q2|}。

S中的最接近点对或者是{p1,p2}，或者是{q1,q2}，或者是某个{p3,q3}，其中p3∈S1且q3∈S2。

                                     

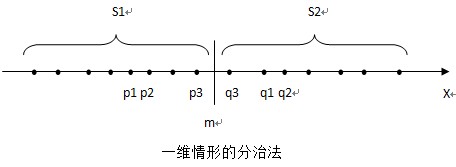
如果S的最接近点对是{p3,q3}，即|p3-q3|<d，则p3和q3两者与m的距离不超过d，即|p3-m|<d，|q3-m|<d。

可得，p3∈(m-d,m]，q3∈(m,m+d]。

由于在S1中，每个长度为d的半闭区间至多包含一个点（否则必有两点距离小于d）。

并且m是S1和S2的分割点，因此(m-d,m]中至多包含S中的一个点，且为S1中最大点。

同理，(m,m+d]中也至多包含S中的一个点，且为S2中最小点。

因此，我们用线性时间就能找到区间(m-d,m]和(m,m+d]中所有点，即p3和q3。

按这种分治策略，合并步可在O(n)时间内完成。

还需考虑的一个问题：分割点m的选取，及S1和S2的划分。

• 选取分割点m的一个基本要求是由此导出集合S的一个线性分割。
• 即S=S1∪S2 ，S1∩S2=Φ，且S1={x|x≤m}；S2={x|x>m}。
• 容易看出，如果选取m=[max(S)+min(S)]/2，可以满足线性分割的要求。
• 选取分割点后，再用O(n)时间即可将S划分成S1={x∈S|x≤m}和S2={x∈S|x>m}。

划分可能出现的问题：造成划分出的子集S1和S2的不平衡

• 例如在最坏情况下，|S1|=1，|S2|=n-1。
• 由此，产生的最坏情况下所需的计算时间T(n)=T(n-1)+O(n)。
• 该递归方程的解为：T(n)=O(n^2)
• 可用分治法中“平衡子问题”的方法来解决，如用S的n个点的坐标的中位数来作分割点。
• 用选取中位数的线性时间算法，可在O(n)时间内确定一个平衡的分割点m。

确定平衡点采用m=[max(S)+min(S)]/2的方法，程序如下：

#include <ctime>
#include <iostream>

using namespace std;

//点对结构体
struct Pair {
    float d;//点对距离
    float d1, d2;//点对坐标
};

float Max(float s[], int p, int q);

float Min(float s[], int p, int q);

template<class Type>
void Swap(Type &x, Type &y);

template<class Type>
int Partition(Type s[], Type x, int l, int r);

Pair Cpair(float s[], int l, int r);

int main()