算法分析——最接近点对问题_最接近点对问题算法-优快云博客

本文链接：https://blog.youkuaiyun.com/ACMer_y/article/details/133875615

本文介绍了如何使用分治策略解决一维和二维最接近点对问题，包括一维问题的简单处理和二维问题中跨边界归并的解决方案，以及利用鸽舍原理优化查找过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

问题描述

在现实世界中，涉及点、圆等几何对象的问题，往往需要了解邻域中其他几何对象的信息。如，判断空中飞行的两架飞机是否有碰撞危险，我们可以将飞机近似为点，它们的最小安全距离就是我们的求解目标，这类问题在计算几何学中被称为最接近点对问题。

当然，我们可以通过遍历的方式来解决这类问题：依次求出平面上散落点两两之间的距离，通过排序找到最近接点对。

这样有个明显的问题：算法的时间复杂度 $T(n)=O(n(n-1)/2)=O(n^2)$ ，为了提高计算效率，考虑通过分治法解决问题。

一维最接近点对问题

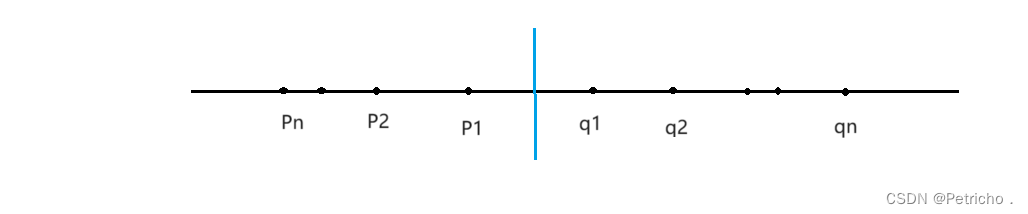
一维最接近点对问题的解决很简单，利用分治策略将点集S划分，求出最邻近点对后逐步合并。当问题规模为n/2时，也就是S被划分为两个子集p和q，并找到其各自的最小点对时无需再将问题合并，只用比较分界线两侧的点距和 $min\{min(p),min(q)\}$ ，较小值即为所求的最接近点对。

核心代码如下：

Pair Cpair(float s[],int l,int r)  
{  
    Pair min_d={99999,0,0};//最短距离  
  
    if(r-l<1) return min_d;  
    float m1=Max(s,l,r),m2=Min(s,l,r);  
  
    float m=(m1+m2)/2;//找出点集中的中位数  
  
    //将点集中的各元素按与m的大小关系分组  
    int j = Partition(s,m,l,r);  
  
    Pair d1=Cpair(s,l,j),d2=Cpair(s,j+1,r);//递归  
    float p=Max(s,l,j),q=Min(s,j+1,r);  
  
    //返回s[]中的具有最近距离的点对及其距离  
    if(d1.d<d2.d)  
    {  
        if((q-p)<d1.d)  
        {  
            min_d.d=(q-p);  
            min_d.d1=q;  
            min_d.d2=p;  
            return min_d;  
        }  
        else return d1;  
    }  
    else  
    {  
        if((q-p)<d2.d)  
        {  
            min_d.d=(q-p);  
            min_d.d1=q;  
            min_d.d2=p;  
            return min_d;  
        }  
        else return d2;  
    }  
}

二维最接近点对问题

现在将一维问题拓展，思考寻找平面上最接近点对。

大部分操作同一维问题，重难点在于“跨越分界线”归并问题。令 $d=min\{dl,dr\}$ ，若存在跨越界线的最接近点对，则这两个点一定落在以分界线为中线， $d\times 2d$ 的矩形区域内；由鸽舍定理，这个矩形区域内最多只存在6个点。那具体是哪6个点呢？为了解决这个问题，我们可以将p和P中所有S2的点投影到垂直线l上。由于能与p点一起构成最接近点对候选者的S2中点一定在矩形R中，所以它们在直线l上的投影点距p在l上投影点的距离小于d。由上面的分析可知，这种投影点最多只有6个。因此，若将q和p中所有S的点按其y坐标排好序，则对q中所有点，对排好序的点列作一次扫描，就可以找出所有最接近点对的候选者，对q中每一点最多只要检查p中排好序的相继6个点。

具体算法如下：

bool Cpair2(PointX X[], int n,PointX& a,PointX& b,float& d)  
{  
    if(n<2) return false;  
  
    PointX* tmpX = new PointX[n];  
    MergeSort(X,tmpX,0,n-1);  
  
    PointY* Y=new PointY[n];   
    for(int i=0;i<n;i++) //将数组X中的点复制到数组Y中  
    {   
        Y[i].p=i;  
        Y[i].x=X[i].x;  
        Y[i].y=X[i].y;  
    }   
  
    PointY* tmpY = new PointY[n];  
    MergeSort(Y,tmpY,0,n-1);  
  
    PointY* Z=new PointY[n];  
    closest(X,Y,Z,0,n-1,a,b,d);   
  
    delete []Y;   
    delete []Z;  
    delete []tmpX;  
    delete []tmpY;  
    return true;   
}