最短路径算法-java实现

最新推荐文章于 2025-05-12 15:39:16 发布

HeinSven

最新推荐文章于 2025-05-12 15:39:16 发布

阅读量1.6k

点赞数 2

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/qq_27437197/article/details/97263027

Java学习笔记专栏收录该内容

13 篇文章

订阅专栏

本文深入解析弗洛伊德算法（Floyd），一种用于解决图中所有顶点对之间的最短路径问题的经典算法。文章首先介绍了算法的基本原理，包括初始化步骤和关键的更新过程，然后通过一个具体的例子演示了如何使用该算法来找到图中任意两点间最短路径的长度及路径本身。此外，还提供了详细的Java实现代码，帮助读者更好地理解和应用这一算法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

弗洛伊德算法(Floyd)：

先初始化，两个矩阵，一个是图的邻接矩阵D，一个是路径矩阵P。

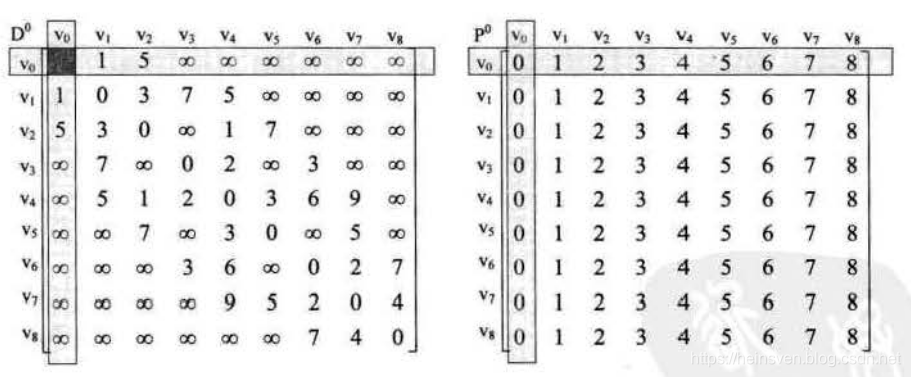
之后，沿着对角线，更新矩阵D和P：

例如：D[0][2]更新为锁定的行列下的，D[0][1]+D[1][2]=4

所以，P[0][2]，从0点到达了2点时，中途还经过了1点，所以P[0][2]

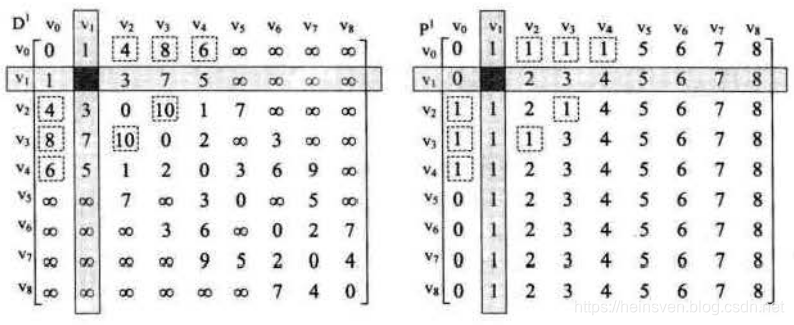
最后计算完，根据P矩阵，复原路径：

例如：P[0][8]=1，说明经过了第一个节点v1，然后再算P[1][8]=2，说明经过了第二个节点v2，以此类推...

public class FloydInGraph {

    private static int INF = Integer.MAX_VALUE;
    private int[][] dist;
    //顶点i 到 j的最短路径长度，初值是i到j的边的权重
    private int[][] path;
    private List<Integer> result = new ArrayList<>();

    public static void main(String[] args) {
        //创建一个5x5的邻接矩阵来存储图
        FloydInGraph graph = new FloydInGraph(5);
        int[][] matrix = {
                {INF, 30, INF, 10, 50},
                {INF, INF, 60, INF, INF},
                {INF, INF, INF, INF, INF},
                {INF, INF, INF, INF, 30},
                {50, INF, 40, INF, INF},
        };
        int begin = 0;
        int end = 4;
        graph.findCheapestPath(begin, end, matrix);
        List<Integer> list = graph.result;
        System.out.println(begin + " to " + end + ",the cheapest path is:");
        System.out.println(list.toString());
        System.out.println(graph.dist[begin][end]);
    }

    public void findCheapestPath(int begin, int end, int[][] matrix) {
        //求出matrix的最短路径
        floyd(matrix);
        result.add(begin);
        findPath(begin, end);
        result.add(end);
    }

    public void findPath(int i, int j) {
        // 找到路由节点
        int k = path[i][j];
        if (k == -1)
            return;
        // 从i到路由节点进行递归寻找中间节点
        findPath(i, k);
        result.add(k);
        // 从j到路由节点进行递归寻找中间节点
        findPath(k, j);
    }

    public void floyd(int[][] matrix) {
        int size = matrix.length;
        for (int i = 0; i < size; i++) {
            for (int j = 0; j < size; j++) {
                path[i][j] = -1;
                dist[i][j] = matrix[i][j];
            }
        }
        for (int k = 0; k < size; k++) {
            for (int i = 0; i < size; i++) {
                for (int j = 0; j < size; j++) {
                    if (dist[i][k] != INF && dist[k][j] != INF && dist[i][k] + dist[k][j] < dist[i][j]) {
                        // 更新i和j两点间的距离
                        dist[i][j] = dist[i][k] + dist[k][j];
                        // 记录从i点到j点序列的，中间第一个节点k
                        path[i][j] = k;
                    }
                }
            }
        }
    }

    public FloydInGraph(int size) {
        this.path = new int[size][size];
        this.dist = new int[size][size];
    }
}