上一篇我们介绍了泰勒公式以及它的证明过程,今天我们来看看一些常用函数的泰勒公式。首先回顾一下:
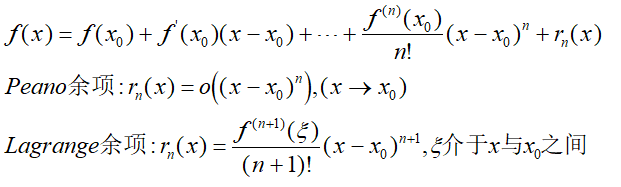
1
对于零点处的泰勒公式,我们又称为麦克劳林公式:
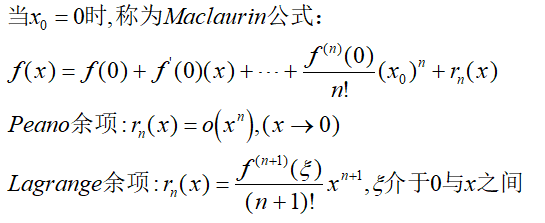
通常情况下,我们只研究函数的麦克劳林公式,因为其他任何的取值都可以转化为在零点的情况:

下面来看几个基本初等函数的泰勒公式。
指数函数

三角函数

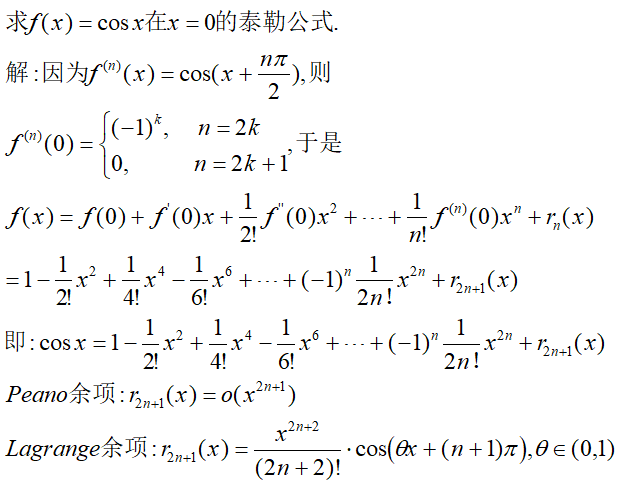
幂函数
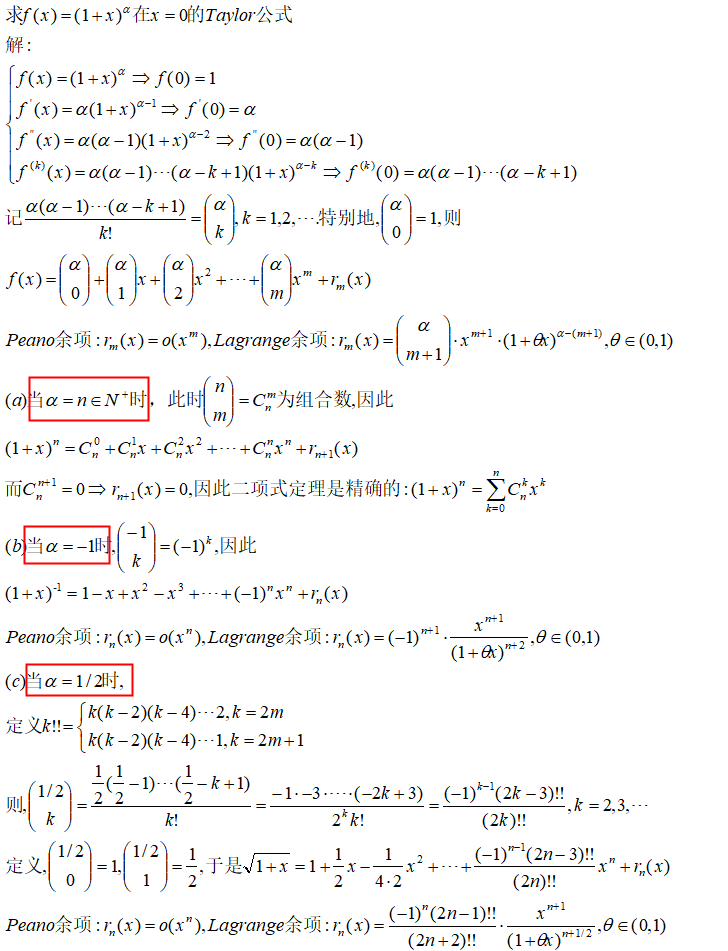
利用上面的公式我们可以求一些复合函数的泰勒公式。举几个例子。
例1

例2

2
对于泰勒公式,我们有定理:

证明非常简单,直接对f(x)的泰勒公式求导即可。这里不再给出。我们来看剩余基本初等函数的泰勒公式。
对数函数

反三角函数

3
泰勒公式应用的范围很广,我们举例来说明!
1.近似计算
我们注意到余项,其实是一个很高阶的无穷小量,它代表用泰勒多项式近似原函数时的误差,这个误差在一定程度代表了近似的精度。利用泰勒公式我们可以计算某些近似值,比如自然底数e:
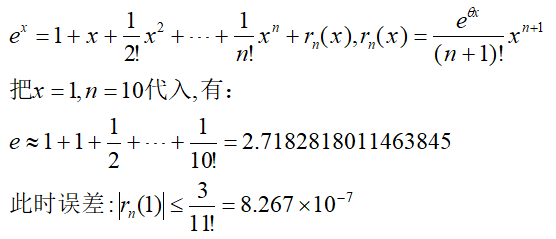
可见,这样估计的误差是很小的,当n取值越大,这个误差就越小。当n趋于无穷时,问题就转化为求数列极限。
泰勒公式计算近似值时并非是所有误差都很小的:

结果到小数点第二位就不精确了。因此,这样的近似结果误差率很大,我们需要另辟蹊径:

2.求极限
泰勒公式在求极限问题上有时候是非常好用的。


3.证明不等式
泰勒公式第三个作用是可以用来证明一些不等式。

4.求曲线渐进性
我们知道,曲线渐近线的充要条件是:

下面看一个例子。

























 25万+
25万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










