Neyman-Person

最新推荐文章于 2025-07-09 16:22:39 发布

原创最新推荐文章于 2025-07-09 16:22:39 发布 · 1.4k 阅读

·

0

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

模式识别专栏收录该内容

3 篇文章

订阅专栏

本文探讨了在限定第二类错误率的前提下，如何寻找最优决策面以最小化第一类错误率的问题。介绍了R1和R2样本区域，以及如何通过调整拉格朗日乘子λ来实现这一目标。并解释了如何使用似然比密度函数求得λ，以及Neyman-Pearson决策规则的应用。最后，通过ROC曲线评估分类方法的性能。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

首先介绍一下背景:

R1 阴性样本区域, R2 阳性样本区域;

w1 阴性样本类别, w2 阳性样本类别;

第一类错误:假阳性 P1(e); 第二类错误: 假阴性 P2(e);

这个问题有两个变量,一个是决策面,一个是拉格朗日乘子

首先目标方程为:在第二类错误为m的情况下,使得第一类错误最小所求得的决策面

min P1(e) s.t. P2(e)=m;

目标方程 min Y=P1(e)+ \lambda (P2(e)-m)

$\LARGE Y=(1-\lambda m)+\int_{R_{1}}[\lambda p(x|w_{2})-p(x|w_{1})]dx$

分别对x和\lambda求偏导数,令他们得0可以得到:

$\LARGE \lambda=\frac{p(x|w_{1})}{p(x|w_{2})}$

而这个决策边界应该使得:

$\LARGE \int_{R1} P(x|w_{2})dx=m$

当然,\lambda的值是很难求得,可以使用似然比密度函数p(l|w2)求得\lambda

$\LARGE P_{2}(e)=1-\int_{0}^{\lambda}p(l|w_{2})dl=m$

由于P(L|w2)>=0 ,P2(e) 是\lambda的单调函数,即当\lambda增加时P2(e)将逐渐减小,当\lambda=0时,P2(e)=1,当\lambda->+无穷,则P2(e)->0, 因此可以采用试探法对几个不同的\lambda 值计算出P2(e)后, 总可以找到一个合适的\lambda值,它刚好能够满足P2(e)=m的条件,又使得P1(e)尽可能小.

决策规则:

$\LARGE \frac{p(x|w_{1})}{p(x|w_{2})}> \lambda , x \in w_{1}$

$\LARGE \frac{p(x|w_{1})}{p(x|w_{2})}< \lambda, x \in w_{2}$

使得\lambda是使决策区域一个阈值,这种在限定一类错误率为常数而使得另一类错误率最小的决策规则称作Neyman-Pearson决策规则.

ROC曲线:Sn为真阳性(1-P1(e))作为纵坐标,假阳性(1-Sp=P2(e))作为横坐标,例如下面的图

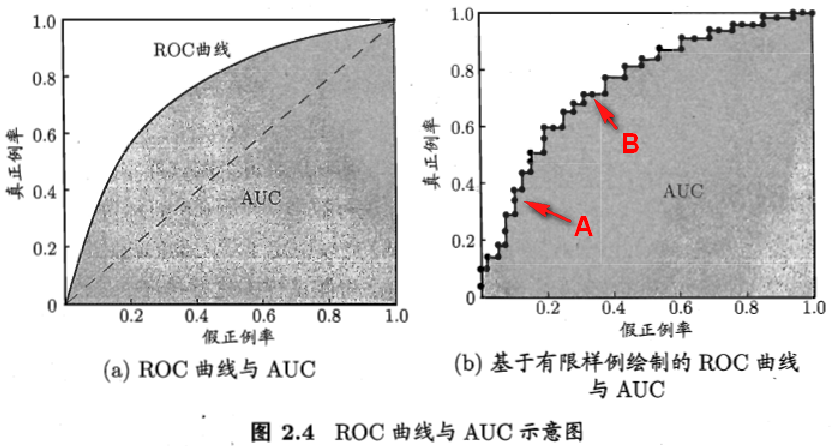
(0.1,0.7)点表示在某一阈值下假阳性为10%时,真阳性为70%.

对于一个决策方法,总是希望真阳性率高,假阳性率低,如果某种方法的真阳性率总是等于其假阳性率,那么就没有任何应用价值,这就是ROC曲线中的对角线,任何分类方法或检验方法,其ROC曲线都必须在对角线左上方可能有实际价值,ROC曲线越靠近左上角,说明方法的性能越好,因此人们通过ROC曲线来全面的评价一种分类方法或者比较两种分类方法的优劣,

评论 1

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。