机器学习|Week3 Logistic Regression and Regularzation

作为英语课程，读中文参考资料的确有助于理解，但是出于对以后更长久的学习优势考虑，笔记中我会尽量采用英文来表述，这样有助于熟悉专有名词以及常见语法结构，对于无中文翻译的资料阅读大有裨益。

Week3 Logistic Regression and Regularzation

一、Logistic Regression

1. Classification分类问题

2. Logistic Regression逻辑回归模型

   • $h_{\theta }(x)=g({\theta }_{T}X)$
     • 对于给定的输入变量X,$\theta$,计算输出变量=1的可能性
     • $h_{\theta }(x)=P(y=1|x;\theta )$
   • X:Feature Vector
   • g:Logistic function/Sigmoid function
     • $g(z)=\frac{1}{1+e^{-z}}$
     • 

3. Decision Boundary决策边界

   1. 根据逻辑回归模型函数可归纳得到

      ${\theta }^{T}x>=0,y=1$

      ${\theta }^T<0,y=0$

4. 如何拟合Logistic Regression的参数$\theta$——Cost Function

   1. We know in Linear Regression
      • $j(\theta )=\frac{1}{m}{\sum }_{i=1}^m\frac{1}{2}(h_{\theta }(x^i)-y^i{)}^2$
   2. In Logistic Regression
      • $J（\theta )=\frac{1}{m}{\sum }_{i+1}^{m}Cost(h_{\theta }(x^i)-y^i)$
        • $Cost(h_{\theta },y)=-log(h_{\theta }(x)),y=1$(成本函数)
        • $Cost(h_{\theta }(x),y)=-log(1-h_{\theta }(x)),y=0$
        • $Cost(h_{\theta },y)=-ylog(h)-(1-y)log(1-h)$
        • 带入J（$\theta$)后得到的J可以证明是一个凸函数，化简后代价函数形式上与Linear Logistic的代价函数一致
        • $J(\theta )=\frac{1}{m}{\sum }_{i=1}^m[h_{\theta }-y]x_j$
      • 
      • Meaning: when y=0 h=0,then Cost=0;when y=0,h=1,then cost->$+\infty$
   3. Octave中的高级函数
      • costFunction自动寻找当前参数的最优高级算法，返回

5. Multiclass Classification——one-vs-all 一对多，多类别分类

   1. 将数据分成1和很多类，仍然是二元分类

      $h_{\theta }(x)=p(y=i|x;\theta );i=1,2...k$

二、Regularization正则化

1. 过拟合问题——与training set高度吻合，但是失去预测意义
2. 解决方案
   • 手动丢弃或者模型选择
   • 正则化，保留所有Features，但是减少参数大小
     • 以多项式拟合为例，过拟合是由高次项导致的，让高次项系数趋于0是解决思想
3. 对J（$\theta$）引入Regularization Parameter（正则化参数）（不对${\theta }_0$进行修正（or called “惩罚”）
   • $J(\theta )=\frac{1}{2m}[{\sum }_{i=1}^m(h_{\theta }(x^i)-y^i{)}^2+\lambda {\sum }_{j=1}^n{\theta }_j^2]$
   • 原理解释：令$\lambda$很大，则为了Cost Function尽量小，所有${\theta }_i(i!=0)$都会减小；但也不能太大，不然所有参数趋于0
4. Regularized Linear Regression正则化的线性回归
   • ${\theta }_0:={\theta }_0-\alpha [\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }-y^i)x_0^i]$
   • ${\theta }_j:={\theta }_j-\alpha [\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }-y^i)x_j^i+\frac{\lambda }{m}{\theta }_j]={\theta }_j(1-a\frac{\lambda }{m})-a\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }-y^i)x_j$
5. Regularized Logistic Regression正则化的逻辑回归
   • $J(\theta )=\frac{1}{m}{\sum }_{i=1}^m[-y^{i}log(h_{\theta })-(1-y^i)log(1-h_{\theta })]+\frac{\lambda }{2m}{\sum }_{j=1}^n{\theta }_j^2$
   • 梯度下降函数与Linear Regression形式上一致

三、Week3 编程练习

1. Logistic Regression

   1. Visuralizing the data

      Function plot(x,y,color,style...)

      plot函数提供的可选线属性如下表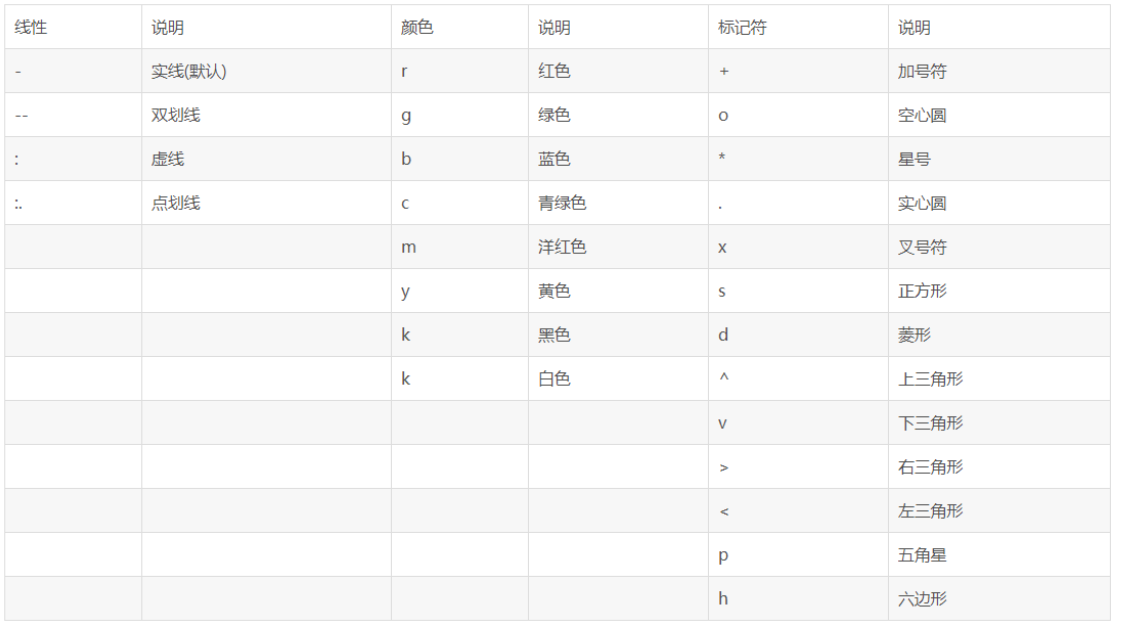

      

      可选全局属性如下

      ​ LineWidth——指定线宽

      ​ MarkerEdgeColor——指定标识符的边缘颜色

      ​ MarkerFaceColor——指定标识符填充颜色

      ​ MarkerSize——指定标识符的大小

      • Find函数

        • Find(X)找到X为真的结果，元素顺序按列排序
        • [row,col] = find(X>0 & X<10,3)，找到矩阵中满足条件得前三个元素，输出[row,col]坐标

      • size

        • 一个返回值返回行、列，向量返回

        • size(A,n)

          如果在size函数的输入参数中再添加一项n，并用1或2为n赋值，则 size将返回矩阵的行数或列数。其中r=size(A,1)该语句返回的是矩阵A的行数， c=size(A,2) 该语句返回的是矩阵A的列数

      • ones（a，b）

        • 输出一个a*b的全1矩阵

      • fminunc Matlab自带的一个高级函数，可以找到最好的$\theta$

      • contour

        • 绘制等高线函数

      • Legend

        • 给画出的图像放上图例

      • Linspace（1，100，2）

        • 产生等差数列

      • matlab逻辑判断为真即可赋值=1

   2. 特别注意，在我编写代码的过程中对于矩阵的转置几次没有仔细查看，导致计算结果错误，这种错有时不会报错，但是你本想获得一个标量，会得到一个矢量；本想获得矢量，变成了标量，这是我对自己很大的一个收获

   3. 参考代码

      1. 写出S函数

         g=1./(1+exp(-z));
         

      2. 求代价函数和相应的$\theta$导数

         J=(-y'*log(sigmoid(X*theta))-(1-y)'*log(1-sigmoid(X*theta)))/m;
         grad = (sigmoid(X*theta)-y)'*X/m;
         

      3. 对模拟数值，求出大于一的预测量

         p = sigmoid(X*theta)>=0.5;
         

      4. 求正则化后的逻辑回归代价函数以及相应的$\theta$导数

     J=(-y'*log(sigmoid(X*theta))-(1-y)'*log(1-sigmoid(X*theta)))/m+lambda*sum(theta(2:size(theta),:).^2)/(2*m);
     grad(2:n)= (sigmoid(X*theta)-y)'*X(:,2:n)/m+lambda*theta(2:n)'/m;
     grad(1)= (sigmoid(X*theta)-y)'*X(:,1)/m;
     ```

     ​