作为英语课程,读中文参考资料的确有助于理解,但是出于对以后更长久的学习优势考虑,笔记中我会尽量采用英文来表述,这样有助于熟悉专有名词以及常见语法结构,对于无中文翻译的资料阅读大有裨益。
一、Cost function and Backpropagation
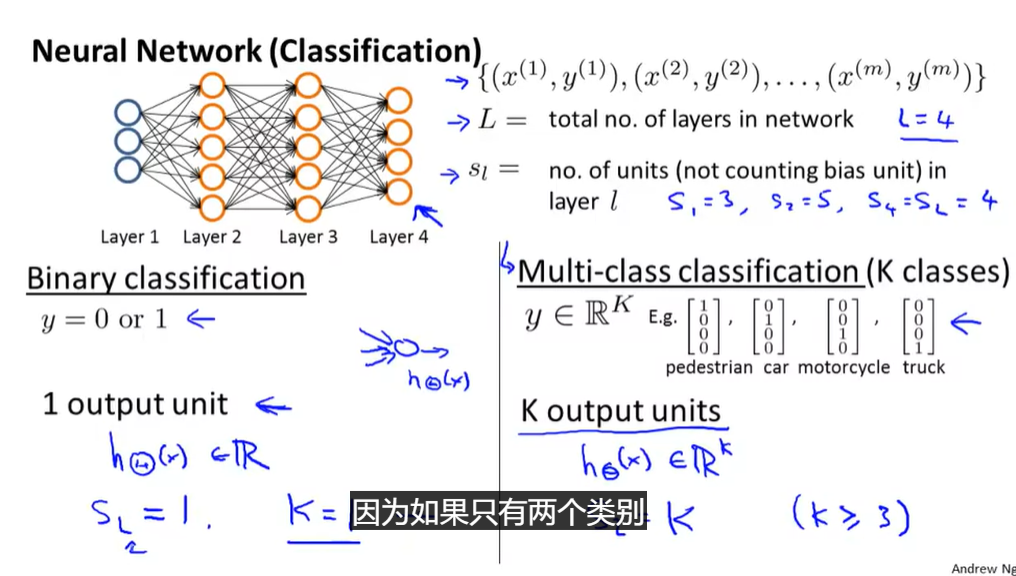
- L:总层数
- S l S_l Sl:第几层

- 上式进行一般化
- y i y^i yi原本是一个逻辑输出单元->取而代之的是K个 y k i y_k^i yki
- 输出值h->向量 h Θ h_\Theta hΘ,记( ( h Θ ) i (h_\Theta)_i (hΘ)i)是此向量的第i个元素
- 括号中的值是对最后一层输出的所有y值进行了求和,正则化一项是将所有l,i,j全部加起来
- 对于i=0的项,不进行正则化,这里没有加进去,即使加上去也没什么影响
J ( Θ ) = − 1 m [ ∑ i = 1 m ∑ k = 1 K y k ( i ) log ( h Θ ( x ( i ) ) ) k + ( 1 − y k ( i ) ) log ( 1 − ( h Θ ( x ( i ) ) ) k ) ] & + λ 2 m ∑ l = 1 L − 1 ∑ i = 1 s l ∑ j = 1 s l + 1 ( Θ j i ( l ) ) 2 \begin{aligned} J(\Theta)=&-\frac{1}{m}\left[\sum_{i=1}^{m} \sum_{k=1}^{K} y_{k}^{(i)} \log \left(h_{\Theta}\left(x^{(i)}\right)\right)_{k}+\left(1-y_{k}^{(i)}\right) \log \left(1-\left(h_{\Theta}\left(x^{(i)}\right)\right)_{k}\right)\right]\&+\frac{\lambda}{2 m} \sum_{l=1}^{L-1} \sum_{i=1}^{s_{l}} \sum_{j=1}^{s_{l+1}}\left(\Theta_{j i}^{(l)}\right)^{2} \end{aligned} J(Θ)=−m1[i=1∑mk=1∑Kyk(i)log(hΘ(x(i)))k+(1−yk(i))log(1−(hΘ(x(i)))k)]&+2mλl=1∑L−1i=1∑slj=1∑sl+1(Θji(l))2
-
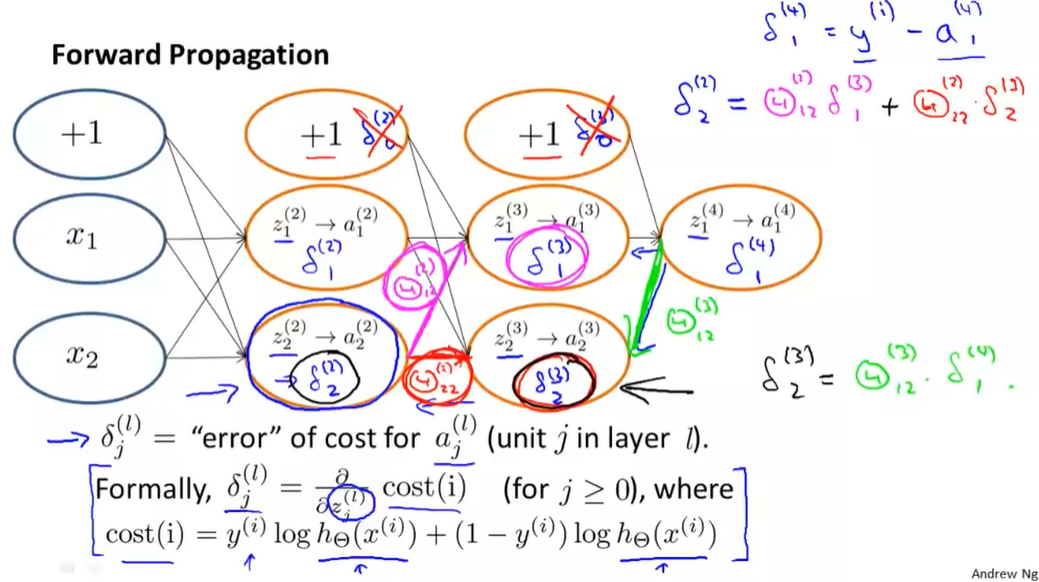
Backpropagation反向传播算法
- 为了计算导数项

-
δ \delta δ=a-y:差值
-
δ ( 3 ) = ( Θ ( 3 ) ) T δ ( 4 ) ∗ g ′ ( z ( 3 ) ) \delta^{(3)}=\left(\Theta^{(3)}\right)^{T} \delta^{(4)} * g^{\prime}\left(z^{(3)}\right) δ(3)=(Θ(3))Tδ(4)∗g′(z(3))
- g ′ ( z 3 ) = a 3 ( 1 − a 3 ) g^{\prime}(z^3)=a^3(1-a^3) g′(z3)=a3(1−a3)
-
∂ ∂ θ i j ( l ) J ( Θ ) = a j ( l ) δ i l + 1 \frac{\partial}{\partial \theta_{i j}^{(l)}} J(\Theta)=a_{j}^{(l)} \delta_{i}^{l+1} ∂θij(l)∂J(Θ)=aj(l)δil+1
- l l l当前计算层
- j j j当前激活单元下标,下一层的第 j j j个输入变量的下标
- i i i下一层误差单元的下标
-
这里没有 δ 1 \delta_1 δ1,因为不需要考虑输入层误差项
-
考虑正则化后,引入 Δ i j l \Delta_{ij}^l Δijl

- 有了 Δ \Delta Δ后,可以计算cost function的偏导数,如上图
FP and BP compare
-
FP
-
-
图中忽略了偏置单元,但这本质是由算法决定的,你有可能需要有可能不需要,大多数情况下bias=1,求导=0,都是直接丢弃的
二、Backpropagation Practice
-
系数从矩阵展开到向量
-
通过(;)将矩阵展开为1列向量
-
通过reshape来重塑矩阵
-
-
Gradient Checking
-
为了避免“一些小bug导致看起来J在下降,但实际得到的误差非常大”
-
ϵ \epsilon ϵ一般在 1 0 − 4 10^{-4} 10−4
-
一般用双边导数而非单边导数(双边准确率更高)
-

-
【注意】一旦checking完成,确认gradient没有问题,真正进入计算时务必关掉checking函数,否则低效率会让你无法忍受(hhhh)
-
Once you have verified once that your backpropagation algorithm is correct, you don’t need to compute gradApprox again. The code to compute gradApprox can be very slow
-
-
-
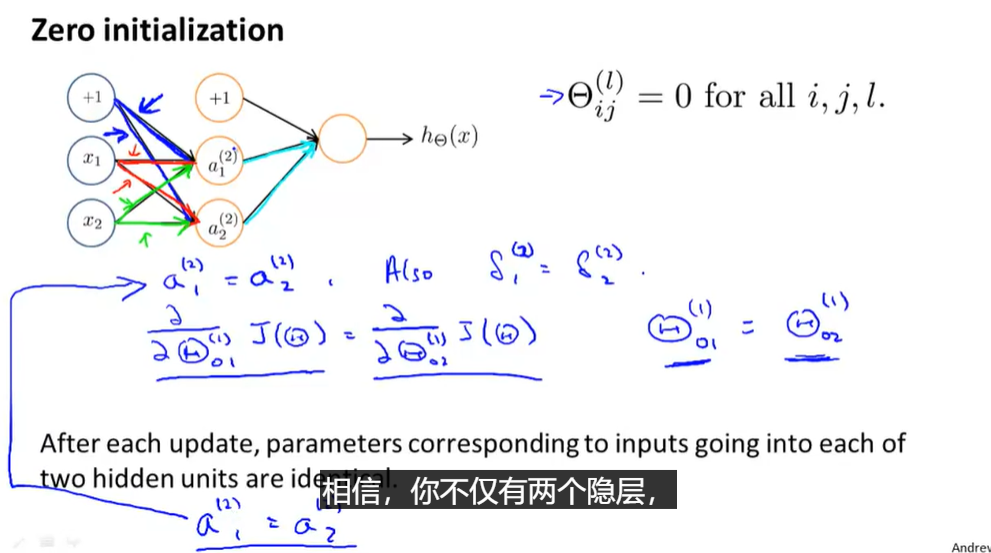
Random Initialization
- 对称现象
-
- 所以初始化也称为“打破对称”(Symmetry Breaking)
- 使用rand函数和 ϵ \epsilon ϵ(与之前无关)确定范围在 [ − ϵ , ϵ ] [-\epsilon,\epsilon] [−ϵ,ϵ]
- 对称现象
-
Putting it Together(回顾)
-
搭建神经网络:可选多少个隐藏层,每个隐藏层有多少个隐藏单元
- 搭建规则:Reasonable default:1 hidden layer,or if >1 hidden layer,have same no. of hidden units in every layer(usually the more the better)
-
训练过程
-
Randomly initialize weights:初始化权值,通常是很小的接近于0的数
-
implement FP for any input x i x^i xi and its h ( x i ) h(x^i) h(xi)
-
compute J ( Θ ) J(\Theta) J(Θ)
-
implement BP to compute partial derivatives ∂ ∂ Θ j k l J ( Θ ) \frac{\partial}{\partial\Theta_{jk}^l}J(\Theta) ∂Θjkl∂J(Θ)
- 对所有的m个样本执行上述训练过程
-
Gradient Checking to compare ∂ ∂ Θ j k l J ( Θ ) \frac{\partial}{\partial\Theta_{jk}^l}J(\Theta) ∂Θjkl∂J(Θ) ,确定二者接近后,关闭Checking
-
使用优化算法结合BP计算出所有偏导数项,继而将cost Function J ( Θ ) J(\Theta) J(Θ)最小化
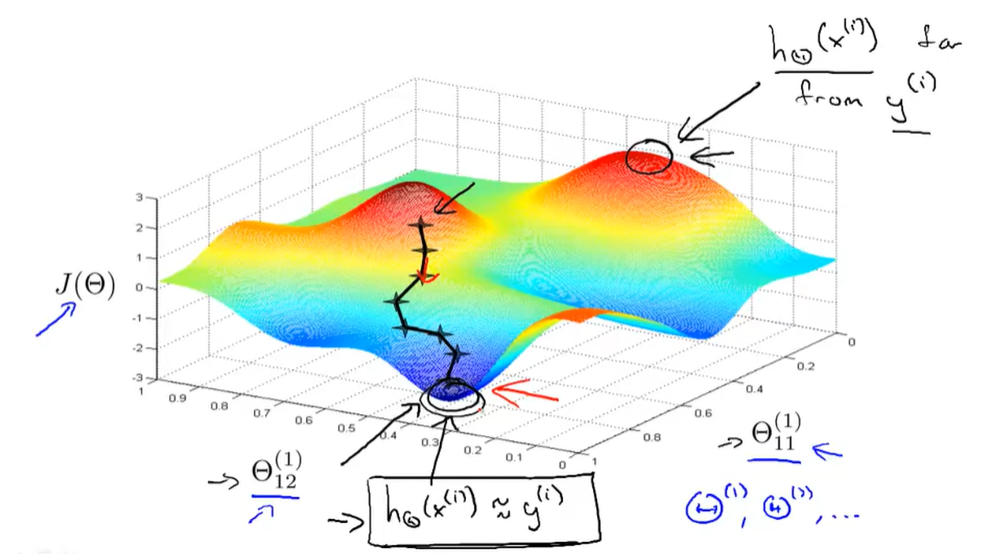
- 对于neural Network,J并非一个凸函数,理论上是可能停留在局部最小的,不过通常此影响不大,即便不是全局最小值也会得到一个很小的局部最小值
-
-
三、Application of Neural Networks
Autonomous Driving
四、编程作业
BP算法写出,注意除以m的时候不要误写






 本文详细介绍了神经网络的成本函数和反向传播算法,包括成本函数的数学表达式和反向传播的计算过程。还讨论了梯度检查、随机初始化的重要性,以及神经网络在自动驾驶等领域的应用。同时,强调了在编程作业中实现BP算法的注意事项。
本文详细介绍了神经网络的成本函数和反向传播算法,包括成本函数的数学表达式和反向传播的计算过程。还讨论了梯度检查、随机初始化的重要性,以及神经网络在自动驾驶等领域的应用。同时,强调了在编程作业中实现BP算法的注意事项。

















 5327
5327

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








