【深度学习基础-06】支持向量机SVM（下）-线性不可分

最新推荐文章于 2024-06-11 15:17:35 发布
最新推荐文章于 2024-06-11 15:17:35 发布
阅读量1.9k 收藏
点赞数
CC 4.0 BY-SA版权
分类专栏： 深度学习基础专栏 由浅入深学习机器学习 文章标签： SVM
学习记录
本文链接：https://blog.youkuaiyun.com/qq_15698613/article/details/86101273
SVM作为机器学习中的经典算法，其优点在于训练模型复杂度取决于支持向量，不易过拟合。在面对线性不可分的数据时，通过非线性映射将数据映射到高维空间，使得分类变得可能。本文探讨了如何解决线性不可分问题以及如何进行多类问题的分类。后续内容将涉及具体实现和代码学习。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

 1 SVM的优点

                                     

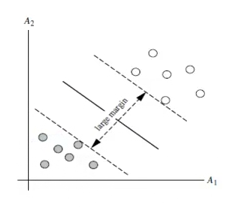
训练好的模型算法复杂度是由支持向量的个数决定，而不是数据维度决定，所以SVM不太容易过拟合。

SVM训练出来的模型完全依赖于支持向量，即使训练集里面所有非支持点都去除，重复训练过程，结果模型完全一样

一个SVM如果训练得到的支持向量个数少，则模型更容易泛化（比如各有1个点，剩下的所有可以随便扔）

2 针对线性不可分情况

数据集在空间中对应的向量不可以被一个超平面分开

2.1 如何解决？

 

  1. 利用一个非线性的映射，把原数据集中的向量点转化到更高维度的空间中
  2. 在这个高纬度空间找一个线性超平面来根据线性可分的情况处理

                         &n

了解本专栏 订阅专栏 解锁全文
支持向量机SVM(2)-线性不可分时的线性支持向量机
xu_aml的博客
05-10 928
支持向量机__线性不可分时的线性支持向量机 假设给第一个特征空间上的训练数据集T={(x1,y1),(x2,y2),⋯ ,(xN,yN)} T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}T={(x1​,y1​),(...
机器学习(18)之支持向量机原理(三)线性不可分支持向量机与核函数
机器学习算法与Python学习
09-24 1244
微信公众号关键字全网搜索最新排名【机器学习算法】：排名第一【机器学习】：排名第二【Python】：排名第三【算法】：排名第四前言在（机器学习（15）之支持向量机原理(一)线性支持向量机）和（机器学习(16)之支持向量机原理(二)软间隔最大化）中我们讲到了线性可分SVM的硬间隔最大化和软间隔最大化的算法，它们对线性可分的数据有很好的处理，但是对完全线性不可分的数据没有办法。本文我们就来探讨SVM如何
线性可分情形下支持向量机学习的SMO算法
LJBlog2014的专栏
10-12 1299
求解上述优化模型
支持向量机对线性不可分数据的处理
xw20084898的专栏
03-25 7124
目标 本文档尝试解答如下问题: 在训练数据线性不可分时，如何定义此情形下支持向量机的最优化问题。如何设置 CvSVMParams 中的参数来解决此类问题。 动机 为什么需要将支持向量机优化问题扩展到线性不可分的情形？ 在多数计算机视觉运用中，我们需要的不仅仅是一个简单的SVM线性分类器， 我们需要更加强大的工具来解决 训练数据无法用一个超平面分割 的情形。 我们以
深度学习基础（三）--SVM
向前方，莫转角
09-29 672
总结一下今天的学习过程 今天可以说是不充实，荒废的好多时间 1，今天干一些无关学习的事，这里就不多说了 2，中午和下午就感觉比较坑了，以前安装工具都是百度，这好不容易感觉上道了，说是看个文档吧，结果还安装错了，还是走了好多弯路       本意是在Anaconda3中安装numpy以及pylab，按照着Anaconda3中自带的Python3.6.1documentaction这个文档安装
机器学习之深度学习基础--支持向量机（SVM）视频教学
06-09
支持向量机（Support Vector Machine，SVM）是机器学习领域的一种强大算法，尤其在分类和回归任务中表现优秀。SVM的核心思想是找到一个最优的超平面，以最大化数据点到该超平面的距离，从而实现对数据的有效划分。在...
实战案例-使用支持向量机（SVM）算法进行人脸识别
06-17
可以直接将两种类型的数据分开），可以将数据分为三种类型，一类是线性可分的、一类是近似线性可分（有一些异常点导致无法线性可分）、一类是线性不可分。 这三种场景对应的SVM的算法分别是硬间隔SVM、软间隔SVM和非...
机器学习--支持向量机（SVM）
最新发布
sdasdfwfsf的博客
06-11 1716
支持向量机（Support Vector Machine，SVM）是一种二分类模型，SVM可以用于线性和非线性分类问题，回归以及异常值检测。其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。支持向量机的学习算法是求解凸二次规划的最优化算法。其基本原理是通过在特征空间中找到一个超平面，将不同类别的样本分开，并且使得离超平面最近的样本点到超平面的距离最大化。
DBN-LSTM-SVM的电池电容预测，基于深度信念神经网络dbn+长短期神经网络LSTM+支持向量机SVM的电池电容预测
08-06
在电池电容预测中，SVM可以处理小样本数据，并且在非线性可分情况下表现优秀。通过在DBN和LSTM学习到的特征上应用SVM，可以进一步提升预测的精度。 在提供的代码中，`funlstm.m` 可能是LSTM网络的实现函数，`rbm1.m...
深度学习基础课程1笔记-支持向量机（SVM）
07-01 2736
本篇内容是xxxx深度学习基础课程视频上的，如有侵权，请与我联系，谢谢！ 一，理论知识 上图中有红绿蓝三条线，那条线分类效果最好呢？明显是红色的线，为什么红线比蓝线效果好呢？ 1）SVM寻找分两类的超平面（hyper plane），使边际（magrin）最大 下图解释一下边际最大： 2）总共可以有多少个可能的超平面？答案是有无数条 如何选取使边际(...
机器学习笔记-线性不可分支持向量机的实现
weixin_54814385的博客
01-15 913
线性不可分支持向量机MATLAB实现
机器学习-支持向量机理论与应用(线性不可分)
diantu6020的博客
02-24 377
1. SVM算法特性 1.1 训练好的模型的算法复杂度是由支持向量的个数决定的，而不是由数据的维度决定的。所以SVM不太容易产生overfitting 1.2 SVM训练出来的模型完全依赖于支持向量(Support Vectors), 即使训练集里面所有非支持向量的点都被去除，重复训练过程，结果仍然会得到完全一样的模型。 1.3 一个...
【机器学习】支持向量机原理(三)线性不可分支持向量机与核函数
造出高达般的人工智能机器人
03-13 1050
　　在前面两篇我们讲到了线性可分SVM的硬间隔最大化和软间隔最大化的算法，它们对线性可分的数据有很好的处理，但是对完全线性不可分的数据没有办法。本文我们就来探讨SVM如何处理线性不可分的数据，重点讲述核函数在SVM中处理线性不可分数据的作用。 1.核函数的引入 　　线性不可分的低维特征数据，我们可以将其映射到高维，就能线性可分。如下图，二维的低维特征数据是线性不可分的，但是通过核函数k...
[机器学习]解决支持向量机线性不可分问题——核函数II
m0_45164809的博客
11-13 1750
问题 之前在 支持向量机I 中介绍支持向量机通过在样本空间找到一个划分超平面实现将样本分类。但现实任务中，原始样本空间可能不存在一个能正确划分两类样本的超平面。 对于这种问题，可将样本从原始空间映射到一个更高维特征空间，使样本在该特征空间线性可分。 关键准则： 若原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分。 目标函数 划分超平面模型： f(x)=wTϕ(x)+bf(x)=w^T\phi (x)+bf(x)=wTϕ(x)+b 目标函数： minw,b12∥w∥2s.t.yi(wT
吴恩达-机器学习课后题06-SVM(支持向量机)2-线性不可分2-寻找最优gamma
weixin_42673117的博客
12-22 242
1、问题 找出最优化gamma 2、解题 1、导入数据 mat = sio.loadmat(path) # print(mat.keys()) X,y = mat['X'],mat['y'] Xval,yval = mat['Xval'],mat['yval']#验证集 2、数据可视化： #数据可视化 def plot_data(): plt.scatter(X[:,0],X[:,1],c=y.flatten(),cmap='jet') plt.xlabel('x1') plt.y
【深度学习基础-05】支持向量机SVM（上）-线性可分
王博（Kings）的博客
01-09 1694
Support Vector Machine 目录 1背景 2 机器学习的一般框架 3 什么是超平面 4 线性可区分（linear separatable）和线性不可区分（linear inseparatable） 5 如何计算超平面以及举例 1背景 Vladimir N. Vapnik和Alexey 在1963年提出 目前的版本是由Corinna Cortes和Vapnik在1...
支持向量机-线性不可分情况
秦琦琛
05-03 1460
支持向量机——非线性可分情况下的公式推理
每天五分钟机器学习：支持向量机通过核函数解决线性不可分的问题
huanfeng_AI的博客
11-13 1420
当获取到样本的新特征之后，我们就可以使用这个新特征来完成数据的分类了，但是现在还有一个问题，就是标记点l，本例中是随机选取了三个，可实际上是不能随机选取的，那么如何选取呢？
SVM解释：四、线性不可分的情况
热门推荐
guoziqing506的博客
07-23 2万+
之前的博客介绍了在数据为线性可分的情况下，如何用SVM对数据集训练，从而得到一个线性分类器，也就是超平面WX+b=0WX+b=0WX + b = 0. 但是我已经强调过多次，线性可分的情况有相当的局限，所以SVM的终极目标还是要解决数据线性不可分的情况。解决这种线性不可分的情况基本的思路有两种： 加入松弛变量和惩罚因子，找到“最好”超平面，这里的“最好”可以理解为尽可能地将数据正确分类； 使用...
支持向量机(SVM)原理与线性可分案例
在本资源中，我们聚焦于SVM支持向量分类机的基本原理，特别是在线性可分情况下的应用。" 支持向量机(SVM)是一种监督学习模型，用于分类和回归分析。它基于最大间隔思想，寻找一个能够将不同类别数据点分开的最优...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值