g2o原理及应用（一）

g2o是一个通用的图优化框架。
本文结合论文g2o: A general framework fo graph optimizaiton说明g2o的理论，然后编写一个示例程序，说明g2o的使用方法。

g2o理论：
许多问题可以建模为最小二乘优化的状态估计问题。问题形式如图

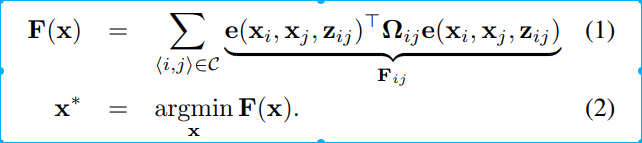
F(x)为目标函数，目的就是求解状态x，使目标函数最小。x是一个向量，向量中的每个元素也可以为一个参数块。zij是联系状态变量i和状态变量j的观测，数学上表现为一个约束方程。由于有测量噪声，采用误差向量e()评价xi和xj满足方程的程度。

论文中为了简化符号，采用下图描述误差向量

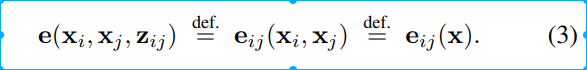
这里需要注意的是，状态变量xi和xj（左侧），已经变为了整个系统的状态x（右侧）。

这个误差向量可以表示为一个有向图，可以知道方程结构，便于可视化分析

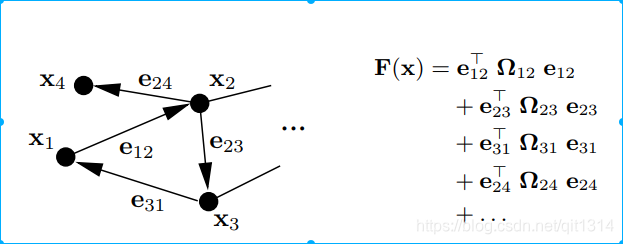
这个图中，边的个数就是所有的约束，也就是方程个数。一个节点为一个状态变量，所有节点的结合组成了整个系统的状态变量。不要忘记我们的目标就是为了状态估计。

有了上述目标函数，我们就可以进行最小二乘优化。
论文中给出的是高斯牛顿法。
高斯牛顿法的思想是：对误差函数e采用一阶泰勒展开。然后构建一个新的误差函数，求这个误差函数的极小值，以极小值作为新的迭代点。重复迭代，直到满足终止条件。