论文速览 | MobiCom 2024 | 单一毫米波雷达实现高精度群体分析 | Crowd Analytics with a Single mmWave Radar

论文速览 | MobiCom 2024 | 单一毫米波雷达实现高精度群体分析 | Crowd Analytics with a Single mmWave Radar

论文链接: https://dl.acm.org/doi/10.1145/3636534.3690664

1 引言

在现代社会中，群体分析已经成为一个至关重要的研究领域。无论是在智慧城市的交通流量管理中，还是在大型集会的安全规划中，甚至是在零售业的客户行为分析中，群体分析都扮演着举足轻重的角色。然而，随着群体规模的增大，传统的分析方法往往力不从心。

本文介绍了一种创新的群体分析方法，它利用单一毫米波雷达来实现高精度的群体分析。这项研究不仅突破了现有技术的局限性，还为群体管理和城市规划提供了新的可能性。

2 动机

传统的群体分析方法主要依赖于视觉系统。虽然这些系统在某些场景下表现出色，但它们也面临着诸多挑战：

1. 隐私问题：视觉系统可能引发公众对隐私保护的担忧。
2. 环境限制：在光线不足或恶劣天气条件下，视觉系统的性能可能大幅下降。
3. 处理能力：对于大规模群体，视觉系统的实时处理能力可能受到挑战。

相比之下，射频（RF）信号，尤其是毫米波信号，为群体分析提供了一个全新的视角。毫米波信号具有以下优势：

1. 隐私保护：不直接采集个人图像，降低了隐私风险。
2. 环境适应性：能够在各种光线和天气条件下正常工作。
3. 高分辨率：相比WiFi等其他RF技术，毫米波信号提供更高的空间分辨率。

然而，利用毫米波信号进行群体分析也面临着独特的挑战，特别是群体遮蔽效应（Crowd Shadowing Effect）。当群体密度增加时，人与人之间的遮挡会导致信号衰减，使得准确计数变得困难。

3 方法

研究团队提出了一套创新的方法体系，旨在解决毫米波雷达在群体分析中面临的挑战。这套方法包括三个主要部分：数学模型、时间卷积网络和自适应阈值处理。让我们深入探讨每个部分的细节。

3.1 数学模型

数学模型是这项研究的核心创新之一。它旨在解决群体遮蔽效应带来的计数不足问题。模型的基本思想是：虽然在任何给定时刻，雷达可能无法观察到所有个体，但通过分析观察到的个体数量的统计分布，我们可以推断出真实的群体规模。

具体来说，模型包括以下关键组成部分：

1. 可见性概率：
   模型首先计算了在N人群体中，任一个体被雷达观察到的概率P(V|N)。这个概率由以下公式给出：

   $P(V|N)=\frac{2}{A^{N-1}(r_{max}^2-{\rho }^2{)}^{-1}(N(N+1)){\rho }^2}\left(\frac{A^{N+1}-(A-\rho \sqrt{r_{max}^2-{\rho }^2}{)}^N}{N\rho \sqrt{r_{max}^2-{\rho }^2}+A}\right)$

   其中，A是感应区域面积，$r_{max}$是最大感应深度，$\rho$是人体半径。

2. 观察分布：
   基于上述可见性概率，模型进一步推导出在N人群体中观察到K人的概率分布：

   $P_a(K|N)=(\genfrac{}{}{0ex}{}{N}{K})P(V|N{)}^K(1-P(V|N){)}^{N-K}$

3. 群体规模估计：
   最后，通过比较理论分布$P_a(K|N)$与实际观察到的分布$P_e(K=\kappa )$，模型使用KL散度来估计真实的群体规模：

   $N^{\ast }=\arg {\min }_{N\in \mathcal{N}}{D}_{KL}(P_e(K=\kappa )||P_a(K=\kappa |N))$

这种方法的优势在于，它不需要精确追踪每个个体，而是通过统计方法来推断群体规模，从而有效地克服了群体遮蔽效应的影响。

3.2 时间卷积网络

对于空间模式化群体，数学模型可能不够有效。因此，研究团队开发了一个时间卷积网络（TCN）。这个网络的设计考虑了以下几个关键点：

1. 输入数据：网络接收二进制轨迹图（Binary Trace Map）$H_{b,vis}$作为输入。这是一个二维矩阵，其中每一列代表一个时间窗口，每一行代表一个深度bin。

2. 网络结构：

   • 两个时间块（TemporalBlock），每个块包含：
     • Conv1D + ReLU层
     • 批归一化（$ϵ=10^{-5}$, $\alpha =0.1$）
     • Dropout（p = 0.5）
   • 残差跳跃连接：避免由填充引起的特征污染

3. 输出和训练：

   • 网络输出每个时间步的残差误差$e[w]=N-n[w]$
   • 使用随机梯度下降进行训练

4. 数据生成：
   为了训练网络，研究团队开发了一个轻量级的群体模拟器。这个模拟器考虑了多种现实因素，如概率性遮蔽、深度不确定性和环境噪声。

5. 应用：
   在实际应用中，网络的输出被用来修正基线估计：$N^{\ast }[w]=n[w]+\mathcal{G}(H_{b,vis})[w]$
   

这种基于TCN的方法不仅能够处理空间模式化群体，还展现出对动态和准动态群体的良好性能。

3.3 自适应阈值处理

为了从原始雷达数据生成高质量的二进制轨迹图，研究团队提出了一种新颖的自适应阈值处理方法。这种方法的核心是一个梯度提升机（GBM）集成。具体步骤如下：

1. 数据收集：
   收集15分钟的同步视频和毫米波雷达数据，包括1、2、5、6人的场景。
   

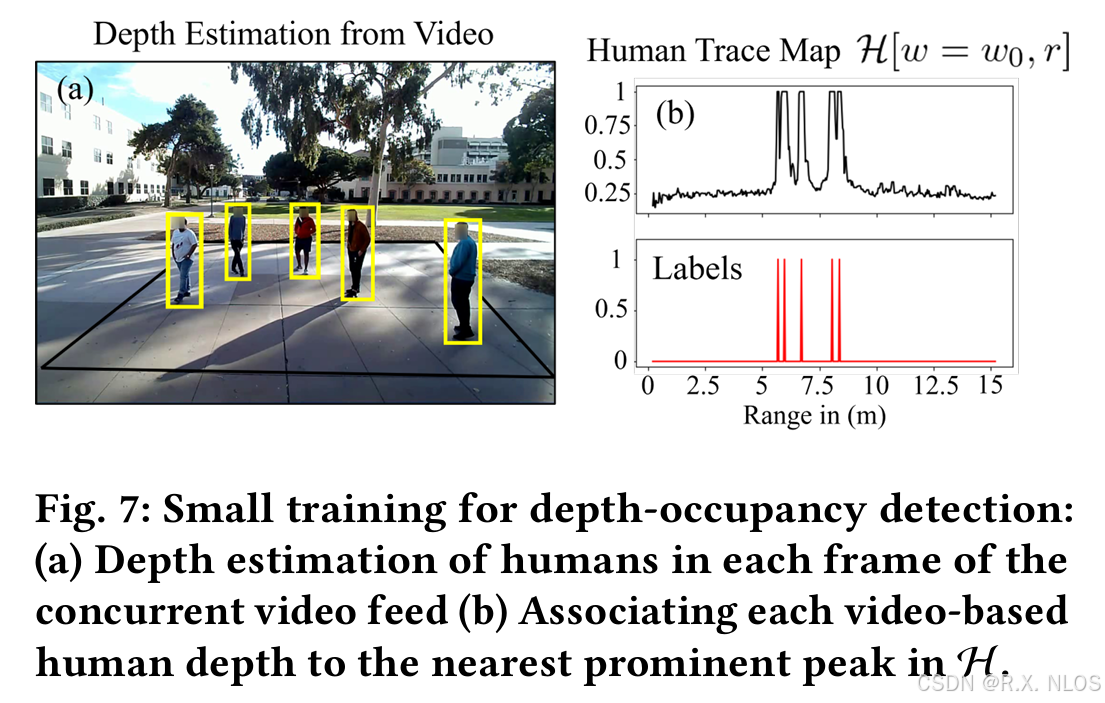
2. 标签生成：
   使用YOLO V5网络从视频帧生成ground-truth二进制标签D[w,r]。

3. GBM训练：

   • 输入：深度r和R_j宽的窗口${\Lambda }_j[w,r]$
   • 输出：二进制标签D[w,r]
   • 使用5折交叉验证进行超参数调优

4. 集成：
   使用4个GBM进行多尺度轨迹检测，窗口大小为$R_j=4{\rho }^j$米，j = 1,2,3,4。

5. 量化：
   将4个GBM的预测组合成量化的人类轨迹图$\hat{H}=(1/4){\sum }_{j=1}^4{D}_j$。

6. 自适应阈值：
   基于初始群体规模估计选择检测阈值，在灵敏度和鲁棒性之间取得平衡。

这种方法不仅能有效地检测人类位置，还能去除噪声，为后续的群体分析提供高质量的输入数据。

4 实验和结果

研究团队进行了广泛的实验来验证所提出方法的有效性。这些实验涵盖了多种群体行为和环境条件，提供了全面的性能评估。

4.1 实验设置

1. 硬件：

   • 使用TI AWR2243BOOST毫米波雷达板
   • 基频$f_0=76GHz$，带宽B = 5GHz，脉冲重复频率$f_c=400Hz$
   • 最大感应深度$r_{max}=15m$

2. 实验区域：

   • 区域1：12.8m × 15m的开放区域，有座位和拖车
   • 区域2：15.2m × 10.2m的建筑屋顶，存在多径效应
   • 区域3：15.1m × 12m的开放区域，周围有大量植被
   • 区域4：10.8m × 15m的室内剧场舞台

3. 群体行为：

   • 动态群体：模拟火车站或繁忙城市广场的场景
   • 准动态群体：模拟海报展或派对场景
   • 空间模式化群体：模拟教室入座或讲座结束后离开的场景
     

4.2 主要结果

1. 动态群体：

   • 进行了9次实验，群体规模最多达21人
   • 数学模型实现了1.44的平均绝对误差（MAE）
   • 相比之下，基线方法（简单平均）在大于10人的群体中MAE达到4.4

2. 准动态群体：

   • 进行了8次实验，群体规模最多达21人
   • 数学模型实现了1.62的MAE
   • 基线方法在大于10人的群体中MAE达到5.3
     
     

3. 空间模式化群体：

   • TCN在处理复杂空间模式时表现出色
   • 例如，准确估计了教室入座和讲座结束后离开的人数变化
     

4. 收敛性分析：

   • 动态群体：平均在75.4秒内收敛到最终估计
   • 准动态群体：平均需要112.7秒收敛，反映了较低的群体移动性

5. 室内性能：

   • 在区域4（室内剧场）中，通过简单校准$r_{max}$，成功计数14人

4.3 额外分析

1. 群体参与度分析：

   • 提出使用可见人数n[w]的自相关函数的第一个零交叉点${\tau }_Z$来衡量群体参与度
   • 动态群体平均${\tau }_Z=9.8s$，准动态群体平均${\tau }_Z=24.4s$
   • 成功区分了不同类型的群体行为

2. 群体异常检测：

   • 模拟了一个紧急疏散场景
   • TCN能够精确检测到突然的群体变化，识别出人数变化率> 3人/秒的异常情况
     

3. 瓶颈推断：

   • 通过观察群体规模随时间的变化率，成功推断出入口的大小
   • 宽入口导致更陡的人数增长曲线，而窄入口则导致更平缓的增长
     

4.4 结果讨论

1. 方法优势：

   • 数学模型在处理动态和准动态群体时表现优异，即使在复杂环境中也能保持高精度
   • TCN展现出对各种群体行为的适应性，特别是在处理空间模式化群体时
   • 自适应阈值处理方法有效地从原始雷达数据中提取有用信息

2. 局限性：

   • 在非常大的群体（>20人）中，估计精度可能会下降
   • 复杂环境中的多径效应可能影响性能，需要进一步研究

3. 潜在应用：

   • 智慧城市中的交通流量管理
   • 大型活动的安全监控
   • 零售业的客户行为分析
   • 公共场所的人流调控

总的来说，这些实验结果充分证明了所提出方法的有效性和适用性。无论是在室内还是室外，无论是动态群体还是准动态群体，该系统都展现出了优异的性能。此外，系统还展示了进行群体参与度分析、异常检测和瓶颈推断的能力，这为其在实际应用中的广泛使用奠定了基础。

5 不足和未来展望

尽管取得了显著成果，该研究仍存在一些局限性和可改进之处：

1. 非视线（NLOS）场景：当前框架主要考虑直接视线情况，未来可以通过增加发射功率或利用环境知识来几何解析多径效应来应对NLOS场景。

2. 大规模群体：对于超过20人的非常大的群体，计数精度可能会下降。未来可以考虑结合可靠的到达角（AoA）信息，实现对特定角度扇区的计数。

3. 复杂群体动态：当前方法没有考虑所有的群体动态，如瞬态场景或群体密度的空间偏差。未来可以通过定制分析模型来应对特定场景，甚至可以利用基于视觉的方法自动学习这些先验知识，以提高占用率估计的准确性。

4. 多径效应：在某些复杂环境中，强反射体可能导致幽灵多径反射（GMRs），影响系统性能。未来可以探索如何有效地识别和消除这些GMRs。

5. 跨场景适应性：虽然当前系统在多个场景中表现良好，但未来还需要在更多复杂和多样化的环境中进行验证和优化。

6. 融合其他传感器：未来可以考虑将毫米波雷达与其他传感器（如低分辨率相机或热成像设备）结合，在保护隐私的同时进一步提高系统性能。

6 总结

这项研究通过巧妙地利用单一毫米波雷达，研究团队成功克服了传统方法面临的诸多挑战，实现了高精度的群体计数和行为分析。

这项技术的核心创新点包括：

1. 新颖的数学模型：通过建立群体遮蔽效应的统计模型，有效解决了大规模群体计数的难题。
2. 灵活的机器学习方法：引入时间卷积网络，扩展了系统对复杂空间模式的处理能力。
3. 创新的信号处理技术：提出自适应阈值处理方法，有效提取有用信息并抑制噪声。

这项研究不仅在技术上取得了突破，其应用前景也令人振奋。从智慧城市的交通管理到大型活动的安全监控，从零售业的客户行为分析到公共场所的人流调控，这项技术都有望带来革命性的变革。

然而，正如任何前沿研究一样，这项技术还有进一步完善的空间。未来的研究方向可能包括提高系统在复杂环境中的鲁棒性、扩展到更大规模的群体、融合多种传感器技术等。