论文速览 | MobiCom 2024 | EiCal: 毫米波天线阵列校准新方法 | Zero-Shot Accurate mmWave Antenna Array Calibration i

论文速览 | MobiCom 2024 | EiCal: 零测量毫米波天线阵列校准新方法 | Zero-Shot Accurate mmWave Antenna Array Calibration in the Wild

论文链接: https://dl.acm.org/doi/10.1145/3636534.3697323

1 引言

本文探讨的是毫米波通信中一个至关重要却常被忽视的环节——天线阵列校准。

想象一下，如果一个交响乐团中的每个乐手都不协调，那么即使是世界上最优美的乐章也会变成噪音。同样地，如果毫米波天线阵列中的每个元件都不能精确地协同工作，那么我们就无法实现精准的波束成形，更别提高效的通信了。

本文提出了一种名为EiCal的创新方法，它巧妙地解决了毫米波天线阵列校准这一棘手问题，而且是以一种零测量、零额外成本的方式实现的。让我们一起深入了解这项可能改变整个行业的技术吧！

2 动机

在深入探讨EiCal之前，我们需要理解为什么天线阵列校准如此重要，以及现有方法存在哪些问题。

2.1 校准的重要性

毫米波通信系统中的天线阵列就像是一支精密的交响乐团。每个天线元件都需要精确地控制其相位和幅度，以便形成所需的波束模式。然而，由于制造误差、元件不一致性等因素，实际的天线阵列往往与理想模型存在偏差。这就好比每个乐手的乐器都有细微的走音，如果不进行校准，整个乐团的演奏就会失去和谐。

2.2 现有方法的局限性

目前，天线阵列校准主要有以下几种方法：

1. 制造商预定义码本：制造商通过在消声室中进行大量测量，提供一组预定义的波束方向和对应的权重向量。这种方法虽然简单，但灵活性很低，无法满足复杂应用的需求。

2. 现场测量校准：通过在实际环境中进行测量来校准天线阵列。这种方法虽然准确，但耗时耗力，而且在已部署的系统中难以实施。

3. 自适应算法：通过实时反馈调整天线参数。这种方法虽然灵活，但计算复杂度高，不适合资源受限的设备。

这些方法就像是在调音时要么只能演奏固定的曲目，要么需要频繁停下来重新调音，要么需要在演奏中不断调整，都不够理想。

2.3 EiCal的创新动机

面对这些挑战，研究团队提出了一个大胆的问题：能否仅利用制造商提供的有限信息，就实现高精度的天线阵列校准？这就像是在问，能否仅通过聆听乐团演奏几首固定的曲目，就能推断出每个乐器的精确调音状态？

这个看似不可能的任务，正是EiCal方法的核心动机。它试图通过巧妙的数学分析，从有限的已知信息中提取出完整的校准信息，实现零测量、零成本的天线阵列校准。这不仅能大大简化校准过程，还能为各种复杂的波束成形应用打开新的可能性。

3 方法

EiCal方法的核心思想可以比喻为从一首交响乐的几个片段中推导出整个乐团的调音状态。让我们深入探讨这个巧妙的方法的每个环节。

3.1 问题建模

首先，我们需要建立一个精确的数学模型来描述天线阵列的行为。假设我们有一个由$N$个元件组成的线性阵列。

3.1.1 理想情况

在理想情况下，要在角度$\theta$形成波束，我们需要给每个元件施加一个特定的相位偏移。这个理想的名义转向向量可以表示为：

$a_{Nominal}(\Omega )=[1,e^{-j\Omega },\cdots ,e^{-j(N-1)\Omega }{]}^T,\Omega =\frac{2\pi d\sin (\theta )}{\lambda }$

其中，$d$是相邻元件间的距离，$\lambda$是信号波长。

3.1.2 实际情况

然而，实际的天线阵列存在各种非理想因素，如制造误差、元件不一致性等。这导致实际的转向向量与理想情况不同。我们可以用一个校准向量$C$来描述这种差异：

$a_{Advertised}(\Omega )=Q(C\odot a_{Nominal}(\Omega ))$

这里，$\odot$表示元素级乘法，$Q(\cdot )$是量化函数，用于模拟实际相移器的离散化效应。

3.2 EiCal算法详解

EiCal的核心思想是从制造商提供的码本中提取出校准向量$C$。这个过程可以分为以下几个关键步骤：

3.2.1 构建矩阵P

首先，我们构建一个矩阵$P$，它是广告码本和理想码本的元素级乘积：

$P=A_{Advertised}\odot A_{Nominal}^{\ast }=[C,\cdots ,C]+\tilde{N}$

这里，$A_{Advertised}$是制造商提供的码本，$A_{Nominal}$是理想码本，$\tilde{N}$是噪声项。

这一步的巧妙之处在于，它将校准问题转化为一个矩阵分析问题。矩阵$P$的每一列理论上都应该是校准向量$C$的一个噪声版本。

3.2.2 奇异值分解（SVD）

接下来，我们对矩阵$P$进行奇异值分解：

$P=U\Sigma V^H$

其中，$U$和$V$是酉矩阵，$\Sigma$是奇异值矩阵。

SVD的作用是将矩阵$P$分解为其主要成分。由于理论上$P$应该是一个秩为1的矩阵（加上噪声），其第一个左奇异向量应该与校准向量$C$高度相关。

3.2.3 提取校准向量

最后，我们将校准向量估计为$P$的第一左奇异向量：

$\hat{C}=u_1$

这里，$u_1$是$U$的第一列，即$P$的第一左奇异向量。

这一步的理论基础是，在噪声较小的情况下，第一左奇异向量应该是最能代表原始信号（即校准向量）的方向。

3.3 生成任意波束模式

有了校准向量，我们就可以生成任意的波束模式了。对于任何期望的波束模式，我们首先计算理想情况下的权重向量$w_{des,nom}$，然后应用校准：

$w_{des,cal}=\hat{C}\odot w_{des,nom}$

这个校准后的权重向量$w_{des,cal}$就是我们实际应用到天线阵列上的值。

3.4 EiCal的创新点

1. 零测量：EiCal不需要额外的测量，完全基于已有的码本信息。
2. 计算效率高：主要计算步骤是SVD，对于现代计算机来说非常快速。
3. 通用性强：适用于任何提供了足够大码本的相控阵系统。
4. 精度高：通过利用所有可用的码本信息，获得了高精度的校准结果。

4 实验和结果

为了全面验证EiCal方法的有效性，研究团队进行了一系列深入而全面的实验。让我们详细探讨这些实验及其结果。

4.1 实验设置

4.1.1 硬件平台

实验使用了Sivers EVK06002板，这是一个60GHz毫米波无线电设备，具有以下特点：

• 16×4的天线阵列
• 6位相移器
• 制造商提供了63个权重向量的码本，覆盖方位角-45°到45°

4.1.2 实验环境

• 辐射模式测量：在一个配有信号吸收材料的受控环境中进行，以最小化多径效应。
• 压缩感知实验：在一个大型开放空间进行，发射机和接收机之间距离为3米。

4.1.3 对比方法

• 无校准：直接使用理想模型，不进行任何校准。
• Nulli-Fi：一种基于多次测量的校准方法。

4.2 校准精度验证

首先，研究团队比较了使用EiCal估计的码本与制造商提供的码本的相似度。

4.2.1 评估指标

使用余弦相似度来衡量估计的码本与真实码本的接近程度：

$\text{similarity}(a_{Adv}(\Omega ),{\hat{a}}_{Adv}(\Omega ))=\frac{|a_{Adv}(\Omega )\cdot {\hat{a}}_{Adv}(\Omega )|}{\Vert a_{Adv}(\Omega ){\Vert }_2\Vert {\hat{a}}_{Adv}(\Omega ){\Vert }_2}$

4.2.2 结果分析

1. 单一权重向量：即使只使用1个权重向量，EiCal也能达到0.92的平均余弦相似度。
2. 16个权重向量：平均余弦相似度提高到0.96。
3. 全部63个权重向量：相似度进一步提高到0.959。

这个结果表明，EiCal具有很强的鲁棒性，即使在信息有限的情况下也能获得良好的校准效果。同时，随着使用的权重向量增多，校准精度也随之提高，但提升幅度逐渐减小，这暗示了在实际应用中可能不需要使用全部的码本信息。

4.3 压缩感知性能评估

研究团队评估了EiCal在压缩感知波束形成中的表现，这是一种用于快速路径发现和到达角估计的技术。

4.3.1 波束模式准确性

1. 评估方法：比较生成的压缩感知波束与理想模式的余弦相似度。
2. 结果：EiCal生成的波束与理想模式的余弦相似度达到0.95以上，显著优于无校准（约0.7）和Nulli-Fi方法（约0.9）。

4.3.2 角度估计精度

1. 实验设置：在不同角度放置发射机，使用压缩感知算法估计到达角。
2. 结果：
   • EiCal：平均角度估计误差为1.29°
   • Nulli-Fi：平均角度估计误差为2.31°
   • 无校准：误差超过10°
     

这些结果清楚地表明，EiCal在压缩感知应用中具有显著优势，不仅能准确地生成所需的波束模式，还能显著提高角度估计的精度。

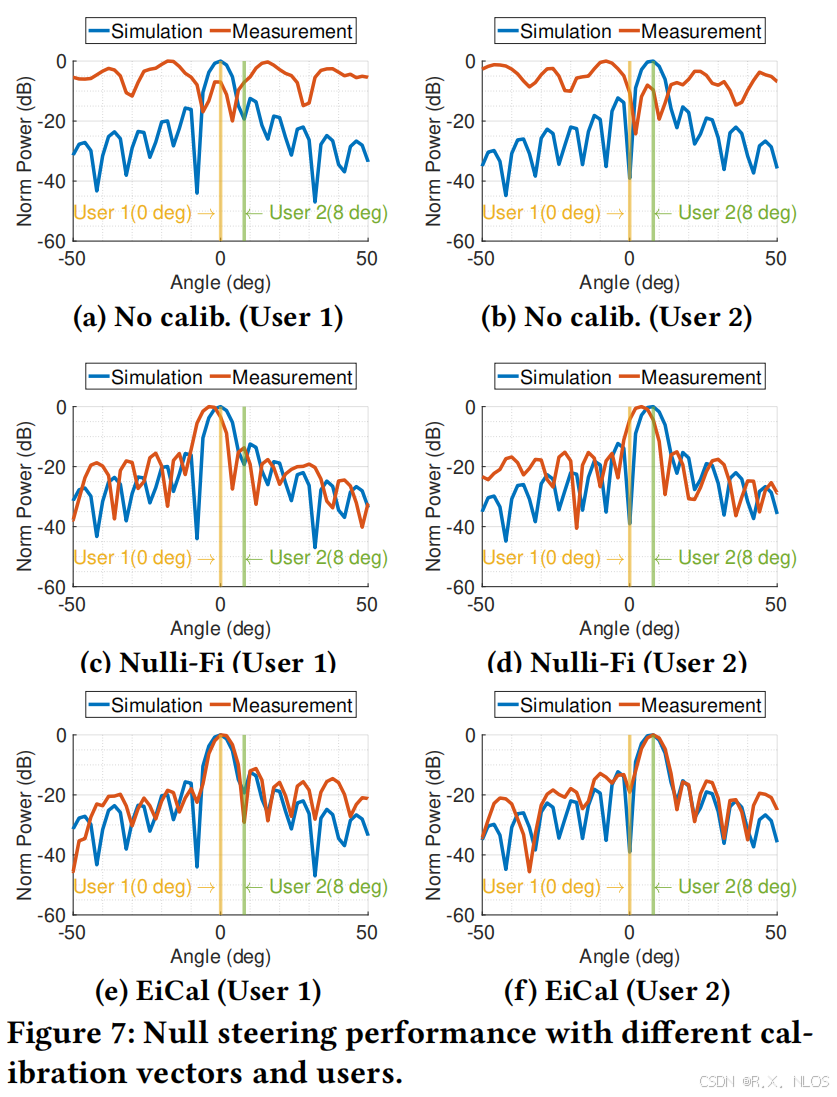
4.4 零点转向性能评估

最后，研究团队评估了EiCal在零点转向任务中的表现，这是一种用于干扰抑制的重要技术。

4.4.1 波束模式相似度

1. 评估方法：比较生成的零点波束与理想模式的余弦相似度。
2. 结果：
   • EiCal：平均余弦相似度为0.9536
   • Nulli-Fi：平均余弦相似度为0.9363
   • 无校准：相似度显著低于0.9

4.4.2 零点深度评估

1. 评估指标：峰值到零点功率比（以dB为单位）
2. 结果：
   • EiCal：
     • 中值零点性能：19.99 dB
     • 最差零点性能：16.74 dB
   • Nulli-Fi：
     • 中值零点性能：15.46 dB
     • 最差零点性能：12.79 dB
   • 无校准：性能显著低于上述两种方法

这些结果表明，EiCal在零点转向任务中也表现出色，能够更准确地形成所需的零点，从而提供更好的干扰抑制能力。

4.5 实验结果总结

通过这一系列全面的实验，我们可以得出以下结论：

1. 高精度校准：EiCal能够从有限的码本信息中提取出高精度的校准向量。
2. 鲁棒性：即使只使用少量的码本信息，EiCal也能获得良好的校准效果。
3. 广泛适用性：EiCal在各种应用场景（基本波束形成、压缩感知、零点转向）中都表现出色。
4. 优于现有方法：在所有测试中，EiCal都显著优于无校准和Nulli-Fi等基线方法。

这些实验结果不仅验证了EiCal方法的有效性，还展示了其在实际应用中的巨大潜力。EiCal为毫米波通信系统的性能优化开辟了一条新的道路，有望在5G/6G通信、车联网、室内定位等领域发挥重要作用。

5 不足和未来展望

尽管EiCal展现出了令人振奋的性能，但我们也需要客观地看待它的局限性，并思考未来的改进方向。

5.1 当前局限性

1. 假设简化：EiCal假设天线元件之间的互耦效应可以忽略，这在某些复杂的阵列结构中可能不成立。就像假设乐器之间没有声音干扰，这在大型管弦乐队中可能不太现实。

2. 依赖制造商码本：EiCal的性能在很大程度上依赖于制造商提供的码本质量。如果码本本身存在问题，EiCal的校准结果也会受到影响。这就像是如果乐谱本身有错误，即使演奏技巧再好也无法弥补。

3. 静态校准：当前的EiCal方法是一种静态校准，没有考虑到天线阵列性能可能随时间、温度等因素变化的情况。这就像是只在演出开始前调音，而忽视了演出过程中可能发生的变化。

5.2 未来研究方向

1. 考虑互耦效应：未来的研究可以尝试将互耦效应纳入模型，以提高在复杂阵列结构中的校准精度。这就像是开发一种能够考虑乐器之间相互影响的更复杂的调音方法。

2. 自适应校准：开发能够实时适应环境变化的动态校准方法，使系统能够随时保持最佳性能。这就像是开发一种能够在演奏过程中不断微调的智能乐器。

3. 扩展到其他阵列结构：将EiCal方法推广到平面阵列、圆形阵列等其他常见的天线阵列结构。这相当于将调音方法从单一乐器扩展到各种不同类型的乐器组合。

4. 结合机器学习：探索将EiCal与深度学习等先进技术结合，以处理更复杂的非线性效应和环境干扰。这就像是开发一种能够学习和适应各种复杂演奏环境的AI辅助调音系统。

5. 硬件协同优化：与硬件设计者合作，探索如何优化天线阵列硬件，使其更适合EiCal这样的软件校准方法。这相当于乐器制造者和演奏者共同优化乐器设计，使其更易于调音和演奏。

6 总结

EiCal方法的提出，无疑为毫米波通信领域带来了一股清新的春风。它巧妙地解决了天线阵列校准这一长期困扰业界的难题，而且是以一种零测量、零额外成本的方式实现的。让我们再次回顾EiCal的主要贡献：

1. 创新的校准思路：通过对制造商提供的码本进行巧妙的数学分析，提取出完整的校准信息。这就像是从几个音符中推导出整个乐谱的和声结构。

2. 高精度校准：在各种实验中，EiCal都展现出了优于现有方法的校准精度，无论是在基本的波束形成还是复杂的压缩感知和零点转向任务中。

3. 实用性强：EiCal不需要额外的测量设备和复杂的操作，可以直接应用于已部署的系统，大大降低了校准的成本和难度。

4. 广泛的应用前景：EiCal为各种复杂的波束成形应用打开了新的可能性，有望推动毫米波通信技术在5G/6G、车联网、室内定位等领域的进一步发展。

当然，EiCal还有进一步改进的空间，特别是在处理复杂阵列结构、适应动态环境变化等方面。但毫无疑问，EiCal的出现标志着毫米波天线阵列校准技术迈出了重要的一步。