模糊AHP与TOPSIS在BI供应商评估中的比较

比较模糊层次分析法和模糊TOPSIS在商业智能供应商评估中的应用

1. 引言

商业智能（BI）是一种信息技术方法，可帮助许多组织做出准确且及时的决策，改进监管过程，从而更好地支持其运营活动、战略与战术规划以及市场细分的预测和分析。通过使用商业智能解决方案，组织能够更便捷地获取信息，并利用分析方法优化其业务绩效。企业价值大幅提升、决策能力改善以及高投资回报是其供应商提出的部分理由。由于这些承诺，许多组织已投资于商业智能。众多商业组织已实现了企业价值的增长，商业智能也取得了令人满意的结果（特班和特班，2007年）。

“商业智能”这一术语在最近十年中变得越来越流行，针对商业智能应用，近期已提出了各种定义，可以说其定义是一场无止境且无定论的争论，不同作者之间存在差异。当前商业智能是一个多层面的概念，可能包括支持更优、更快决策的流程、技术和工具（皮尔蒂马克和汉努拉，2003）。在许多情况下，一些企业正在使用商业智能工具或解决方案，但它们使用了不同的名称，例如管理信息系统（MIS）、决策支持系统（DSS）、主管信息系统（EIS）等（佩吉尔斯‐菲克，2000）。通常，同一组织会无意中将某些系统的部分功能称为“商业智能系统”，例如专注于客户和知识的客户关系管理（CRM）和知识管理，而商业智能系统主要处理的是数据（索尔伯格·索伊伦，2008）。

商业智能系统的用户通常倾向于考虑其商业方面，而非技术方面（布劳提加姆等人，2006）。这类商业智能用户通常负责为其组织选择或参与选择最佳的商业智能系统进行投资。选择商业智能系统是一个复杂且耗时的过程，涉及大量资源和多个部门。决定实施哪种商业智能解决方案以及选用哪家商业智能供应商非常困难，需要对各种备选方案进行彻底的调查和比较。如果没有坚实的推理基础，很难清楚区分供应商所提供的主张与实际提供的论据。以往的研究表明，衡量信息技术投资带来的直接效益是一项困难的任务（福克和奥尔夫，1996）。由于对信息技术领域的投资评估本身具有挑战性，因此在评估和比较不同商业智能工具与系统的供应商时，采用一种显著、有趣且独特的方法将具有重要意义。然而，当前的组织系统是每个组织的基础。

商业智能的设计与实施被视为构建决策支持环境以管理组织系统的统摄性概念。商业系统中对智能工具使用趋势的日益增长，加剧了评估与排序商业智能工具的必要性。据我们所知，目前针对此类工具的排序与评估的研究尚不多见。本研究的结果可显著帮助组织中的管理者和决策者实施商业智能解决方案。我们期望本研究能够帮助管理者和组织更好地理解并选择商业智能工具，有效实施商业智能系统。

本研究的主要目标是确定选择商业智能工具和供应商的关键指标与标准，利用模糊多标准决策方法对商业智能工具进行评估与排序，并最终为样本企业——伊朗国家石油公司推荐合适的机制。

2. 材料与方法

2.1. 研究方法

本研究在目标上属于应用型研究，在方法上属于描述性研究，因为未涉及变量与指标（因素）之间的关系，而是聚焦于伊朗国家石油公司的现状；同时，由于数据来源于伊朗国家石油公司员工，因此也属于调查研究。

详细的方法包括使用描述性和推断性方法来识别有效标准及子准则，应用方法进行供应商排序和优先级划分，以及采用相关研究方法来研究两种方法之间的关系及显著差异。据此，首先通过描述性统计方法识别有效标准，然后应用学生t检验方法对假设进行测试；接着，根据研究目标、显著差异和研究假设，分别采用模糊层次分析法（FAHP）和模糊TOPSIS（FTOPSIS）方法。最后，使用斯皮尔曼相关性检验来研究两种方法之间关系的显著性。

2.1.1. 模糊层次分析法 (FAHP)

扎德（1965年）提出了模糊集理论，以应对由模糊性带来的不确定性。模糊集理论最重要的特征是其能够表达模糊和不确定的数据。梁和曹（2000年）认为，传统层次分析法在获取个人意见时准确性较低的原因之一在于，要求个体基于对现象的理解为两两比较赋予一个确定的数值，而实际上对现象的理解无法用精确的数值来表达，相比之下，使用数值区间能更好地反映个体对某一现象相对于其他现象重要性的理解。因此，模糊层次分析法比传统层次分析法更能模拟人类大脑的决策过程。拉尔霍文和佩德里奇（1983年）首次采用三角模糊数引入了模糊AHP方法。1996年，张提出了一种新的模糊层次分析法分析方法。迄今为止，许多研究人员已在研究中应用了模糊层次分析法，例如用于确定客户需求的重要性（陈等人，2012年）、供应商选择（肖等人，2012年）、ERP顾问的选择（瓦伊瓦伊等人，2012年）、风险评估（王等人，2012年）、商业智能系统绩效评估（雷扎伊等人，2011）以及其他众多问题。本研究所需的步骤包括：

步骤1 通过确定标准、子准则和备选方案来获得层次结构

如前所述，影响商业智能工具排序的标准及子准则，包括3个主准则、19个子准则以及6个备选方案，是通过文献回顾和获取专家对此问题的意见而获得的。

步骤2：以模糊数形式收集专家意见，构建模糊两两比较矩阵，并聚合专家意见

在此阶段，为了收集专家意见，在模糊层次分析法两两比较问卷中使用了有形且通用的表达，而不是传统层次分析法中常用的确定性数值。本研究采用的是特斯法玛丽亚姆和萨迪克（2006年）基于萨蒂量表提出的1‐9三角模糊数标度。在以九分制量表和若干语言表达形式收集专家反馈后，由于无法对定性变量表达式进行数学运算，因此需要将这些反馈转换为可进行分析的量表。因此，语言表达必须转化为模糊标度。三角模糊量表有助于改进决策过程（考夫曼和古普塔，1988年）。表1展示了源自特斯法玛丽亚姆和萨迪克（2006年）研究的语言尺度所对应的模糊数。

表1 语言尺度对应的模糊数

语言变量	模糊数	对应数值的尺度
同等重要	1̃	(1, 1, 1)
两个相邻判断之间的中间值	2̃	(1, 2, 3)
较弱重要	3̃	(2, 3, 4)
两个相邻判断之间的中间值	4̃	(3, 4, 5)
较强重要	5̃	(4, 5, 6)
两个相邻判断之间的中间值	6̃	(5, 6, 7)
极端重要性	7̃	(6, 7, 8)
两个相邻判断之间的中间值	8̃	(7, 8, 9)
绝对更重要	9̃	(8, 9, 9)

三角模糊数如图1和公式(1)所示。一个三角模糊数表示为(l, m, u)。l、m和u分别表示最小可能值、最可能值和最大可能值。

(1) ̃ij = (lij, mij, uij); lij ≤ mij ≤ uij, lij, mij, uij ∈ [1/9, 9]

每个三角模糊数都有一个根据公式(2)所述的隶属函数。模糊对比较矩阵已在公式(3)中给出。

(2)
μŨ(x) = {
(x - l)/(m - l), l ≤ x ≤ m;
(u - x)/(u - m), m ≤ x ≤ u;
0, 其他情况
}

(3)
Ãk = [ãijk], 其中 ãijk 是第 k 位决策者关于 i 和 j 标准之间两两比较的模糊评估值，且 ãijk = (lijk, mijk, uijk)。

两个正三角模糊数Ã和B̃的基本代数运算可总结如表2所示。

表2 两个正三角模糊数Ã和B̃的基本代数运算

操作符	方程	结果
求和	A+B	(l₁ + l₂, m₁ + m₂, u₁ + u₂)
减法	A-B	(l₁‐u₂, m₁‐m₂, u₁‐l₂)
乘法	A×B	(l₁ × l₂, m₁ × m₂, u₁ × u₂)
除法	A/B	(l₁/u₂, m₁/m₂, u₁/l₂)

在为每位专家构建成对比较矩阵后，应对专家意见进行聚合。在本研究中，采用算术平均计算方法（根据公式(4)）对专家的明确意见进行处理，以实现个体意见的聚合，并构建最终成对比较矩阵。

(4)
ãij* = (ãij¹ × ãij² × … × ãijk)^(1/k)

(5)
A = [ãij ]

步骤3：计算一致性比率

研究模糊两两比较矩阵的一致性不像清晰矩阵那样容易。为了解决这个问题，楚斯托拉和巴克利（2001）在其论文中指出，如果 Ã = [ãij] 是使用模糊三角模糊数 ãij = (lij, mij, uij) 构成的模糊两两比较矩阵，则唯一需要做的就是必须确定的是 [mij] 矩阵的一致性。如果A是一致的，则 Ã 也将是一致的。然而，当决策矩阵不完全一致时，在获得矩阵的中间值并使用公式(6)计算 λmax 的最大特征值后，将确定成对比较矩阵的一致性指数：

(6)
CI = (λmax - n) / (n - 1)

如果判断矩阵完全一致，则 λmax = n。矩阵越接近完全一致性，λmax 越接近 n。一致性指数表示决策矩阵的一致性程度。可以看出，该指数与n相关。为了使该指数不受n的影响，应将其除以另一个称为“随机指标”(R.I)的指数。后者指数是通过随机生成的决策矩阵的平均一致性比率计算得出的。表3显示了不同因素数量对应的RI值。这个新指数称为一致性比率(CR)，如公式(7)所示（萨蒂，1990）。

(7)
CR = CI / RI

表3 n决策矩阵各维度的随机指标值

n	3	4	5	6	7	8	9	10	11	12	13	14	15
R.I	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49	1.51	1.48	1.56	1.57	1.59

步骤4：使用CFCS方法计算专家意见聚合矩阵的清晰矩阵

在确保意见一致后，必须将成对比较矩阵从模糊尺度转换为清晰尺度，此过程称为模糊对比较矩阵的去模糊化。针对模糊对比较矩阵的去模糊化，已有多种方法被提出，本文将采用奥普里科维奇和曾国智（2003）提出的方法，利用公式(8‐15)对专家的模糊答案进行去模糊化。若 (lij, mij, uij) 表示第 k 位专家关于第 i 项与第 j 项标准之间两两比较的两两比较矩阵，则 CFCS 方法的步骤如下：

1: Calculating the normalized matrix
(8) xlk = (lkij - lkmin) / Δkmax
(9) xmk = (mkij - lkmin) / Δkmax
(10) xuk = (ukij - lkmin) / Δkmax
其中, Δkmax = ukmax - lkmin

2：计算左侧（ls）和右侧（us）的归一化值
(12) xls = xlk + (1 - xlk)xmk
(13) xus = xuk + (1 - xuk)xmk

3：计算精确的归一化值
(14) xk = [xkls - (1 - xkls)xkus] / [1 + (xkus - xkls)]

4：计算精确值
(15) a*ij = lkmin + xkΔkmax

步骤5：计算最终权重

为了获得权重，采用了萨蒂 (1980) 提出的精确决策矩阵行向量的几何平均值计算方法（见公式(16)）。

(16)
wi = (∏nj=1 a ij)^(1/n) / ∑ni=1 (∏nj=1 a ij)^(1/n), i = 1, 2, …, n

3. 模糊TOPSIS方法(FTOPSIS)

TOPSIS方法首次由王和尹 (1981) 提出。简而言之，该方法中最佳选择是距离正理想点最近且距离负理想点最远的方案。该方法的数据和输入与前述模糊AHP方法类似，即专家意见。在此方法中，专家确定准则或子准则的相对重要性，然后评估每个备选方案在各项准则下的性能。

然而，人类的思维和评价表达常伴随不确定性，这种不确定性会影响决策过程。为解决这一问题，采用了模糊决策方法。在此情况下，决策矩阵元素、准则相对于备选方案的重要性以及准则的重要性（在本问题中）均通过模糊数以模糊方式表达。模糊AHP方法论与模糊TOPSIS方法一样，已被众多研究者应用于多个领域，例如克罗林格和坎帕尼哈罗 (2011) 用于海上溢油事故问题，托尔拉克等人 (2011) 用于土耳其企业竞争力，廖和高 (2011) 用于供应商选择问题，以及凯莱梅尼斯等人 (2011) 用于选择支持经理。用于衡量准则（此处为子准则）重要性以及备选方案（即商业智能软件提供商）在各项准则下性能的模糊与语言尺度见表4和表5（王和埃尔哈格, 2006）。

表4 准则重要性评价的语言尺度

语言重要性	Code	对应的三角模糊数
很低 (VL)	0, 0, 0.1	(0, 0, 0.1)
低 (L)	0, 0.1, 0.3	(0, 0.1, 0.3)
中 (ML)	0.1, 0.3, 0.5	(0.1, 0.3, 0.5)
中等 (M)	0.3, 0.5, 0.7	(0.3, 0.5, 0.7)
中高 (MH)	0.5, 0.7, 0.9	(0.5, 0.7, 0.9)
高 (H)	0.7, 0.9, 1.0	(0.7, 0.9, 1.0)
非常高 (VH)	0.9, 1.0, 1.0	(0.9, 1.0, 1.0)

表5 各子准则下备选方案表现的语言尺度

语言重要性	Code	对应的三角模糊数
很差 (VP)	0, 0, 1	(0, 0, 1)
Poor (P)	0, 1, 3	(0, 1, 3)
中等偏下 (MP)	1, 3, 5	(1, 3, 5)
Fair (F)	3, 5, 7	(3, 5, 7)
中等偏上 (MG)	5, 7, 9	(5, 7, 9)
Good (G)	7, 9, 10	(7, 9, 10)
很好 (VG)	9, 10, 10	(9, 10, 10)

必要模糊TOPSIS方法的实施步骤如下（陈等人，2006）:

步骤1

假设有m个备选方案、n个标准和k位决策者，则模糊多准则决策问题可表示为以下矩阵：

(17)
D̃ = [x̃ij] = [
x̃11 x̃12 … x̃1n
…
x̃i1 x̃i2 … x̃in
…
x̃m1 x̃m2 … x̃mn
]

其中，A1, A2,…，An为需要选择或排名的备选方案；C1, C2,…，Cn为评价准则或特征；x̃ij 表示第k位专家确定的备选方案Ai在准则Cj下的满意度。为了聚合k位专家对x̃ij的模糊绩效得分，采用算术平均数方法，如公式(18)所示：

(18)
x̃ij = (1/k) * (x̃ij¹ + x̃ij² + … + x̃ijk)

其中，x̃ijk 表示第 k 位专家确定的备选方案 Ai 在准则 Cj 下的满意度，且 x̃ijk = (a, b, c)。此外，此步骤还将确定每个子准则的模糊重要性的均值。权重以三角模糊数表示，即 w̃j = (l, m, u)，该数的每个分量分别为专家意见（第一、第二或第三）对应均值。

步骤2：模糊决策矩阵归一化和计算加权归一化模糊决策矩阵

在此步骤中，鉴于在多标准决策问题中，从去除异质单位和各种决策尺度获得的原始数据应进行规范化，因此使用线性规范化来实现此目的。如果R̃是规范化模糊决策矩阵，则我们有：

(19)
R̃ = [r̃ij], i=1,2,…,m; j=1,2,…,n

(20)
r̃ij = (aij/c+j, bij/c+j, cij/c+j), c+j = max(cij), j ∈ B

(21)
r̃ij = (a-j/aij, a-j/bij, a-j/cij), a-j = min(aij), j ∈ C

其中，B 和 C 分别为正向和负向准则的集合。考虑各子准则的不同权重，通过将标准的重要性权重与规范化模糊决策矩阵相乘，计算加权规范化决策矩阵。加权规范化决策矩阵Ṽ定义如下，其中 w̃j 为第j个标准的权重：

(22)
Ṽ = [ṽij], ṽij = r̃ij ⊗ w̃j, i=1,2,…,m; j=1,2,…,n

步骤3：确定正理想解和负理想解

正理想解和负理想解的定义如下：

(23)
A+ = (ṽ1+, ṽ2+, …, ṽn+)
A- = (ṽ1-, ṽ2-, …, ṽn-)

其中：

(24)
ṽj+ = { max(vij), j ∈ J’; min(vij), j ∈ J }

(25)
ṽj- = { min(vij), j ∈ J’; max(vij), j ∈ J }

J = {1,2, …, n}：J 与负向准则相关
J’ = {1,2, …, n}：J’ 相关的正向准则

步骤4：计算每个备选方案到正理想点和负理想点的距离

计算每个备选方案与模糊正理想解和模糊负理想解之间的距离如下所示：

(26)
d+i = Σnj=1 d(ṽij, ṽj+), i=1,2,…,m
d-i = Σnj=1 d(ṽij, ṽj-), i=1,2,…,m

其中，d(ṽij, ṽj+) 表示两个模糊数之间的距离，d+i 表示备选方案i到正理想点的距离，而 d-i 表示备选方案i到负理想解的距离。如果有两个三角模糊数，M(m₁,m₂,m₃) 和 N(n₁,n₂,n₃)，则两数之间的模糊距离计算如下：

(27)
d(M, N) = √[(1/3)((m₁-n₁)² + (m₂-n₂)² + (m₃-n₃)²)]

步骤5：计算接近系数并对备选方案进行排序

通过确定接近系数，将对所有备选方案进行最终排序，决策者可以在多个备选方案中选择最佳方案。各备选方案的接近系数计算如下：

(28)
CCi = d-i / (d+i + d-i), i=1,2,…,m

如果CCi指数接近于1，则备选方案将接近正理想点且远离负理想点。因此，CCi的值越大，Ai的性能越好。

2.2 数据收集方法

为了理解影响商业智能工具的因素和参数并确定此类工具，通过案头研究进行了数据收集，而针对统计总体的数据收集则通过访谈和问卷进行。问卷用于识别商业智能工具的因素和指标（在第二层次），以及准备决策矩阵（用于TOPSIS方法），同时进行数据收集为层次分析法进行的

2.3 统计总体、抽样和样本量

统计总体包括伊朗国家石油公司在信息技术领域的专家。考虑到统计总体中包含的样本数量，为了获得更准确的结果，采用了普查抽样技术。有关影响商业智能工具及商业智能工具选择的因素和参数的数据通过文献回顾收集。同时，关于统计总体的数据通过访谈和问卷的方式进行收集。在确定准则和指标时，采用普查抽样方法，利用伊朗国家石油公司30名IT专家的意见；而通过层次分析法和模糊TOPSIS问卷，并结合抽样技术，获取了七位商业智能专家的意见，用于对标准、子准则以及备选方案进行评估与排序。

2.4 数据分析方法与工具

本研究使用算术平均数（描述性统计）进行数据分析，以确定和识别影响参数与因素；采用模糊层次分析法和模糊TOPSIS方法来识别并排序商业智能工具；利用斯皮尔曼等级相关检验对假设进行测试，以比较两种方法。本分析所使用的应用程序包括SPSS、Excel、Expert Choice和Matlab。所采用的数据分析方法如下所示：
1. 学生T检验作为推论检验，用于确定和识别影响因素及指标。
2. 模糊AHP方法用于评估和优先排序与智能工具与解决方案供应商相关的指标。
3. 模糊TOPSIS方法用于根据伊朗国家石油公司专家意见对商业智能工具和解决方案供应商进行排序。
4. 斯皮尔曼等级相关检验用于评估和比较两种方法（即模糊层次分析法和模糊TOPSIS方法）之间关系的显著性。

2.5 研究范围

本研究的主题范围是评估与排序与商业智能工具和解决方案相关的标准、子准则和备选方案。
本研究的空间范围是伊朗国家石油公司，该公司是伊朗最大的石油和石油产品生产商。本研究的时间范围涵盖2012年3月至2012年9月的6个月期间。

2.6 研究局限性

本研究的主要局限性在于获取专家意见的复杂性。另一个问题是，理论上还可以考虑更多未包含在本研究中的标准、子准则或商业智能工具。然而，由于层次分析法中对于n个因素的两两比较数量由n(n-1)/2决定，随着因素或方案数量的增加，两两比较的数量将急剧上升，这会导致问卷项目数量显著增加，专家可能因此拒绝回答。组织内商业智能专家数量不足以及他们对本文所使用的方法与概念缺乏相关知识，使我们不得不对问卷内容进行解释并开展访谈，从而导致数据收集耗时更长。

2.7 研究实施阶段

本研究按以下阶段进行，图1展示了研究的执行模型：

第一阶段：有效准则及子准则的识别
- 通过案头研究识别重要标准
- 使用李克特量表问卷收集专家意见，利用学生t检验方法检验假设，并确定和选择有效标准、子准则及备选方案

第二阶段：实施模糊AHP方法对商业智能工具和解决方案进行评估与排序
- 准备标准、子准则和备选方案的层次结构并进行编码
- 在第二阶段确定准则、子准则及有效工具后创建层次树模型
- 针对语言尺度设计模糊AHP问卷
- 以模糊数形式收集专家意见，构建模糊两两比较矩阵，并聚合专家意见（7人）
- 计算两两比较的一致性比率
- 使用 CFCS方法对专家意见聚合矩阵进行去模糊化，得到清晰矩阵
- 计算最终权重

第三阶段：实施模糊TOPSIS方法以评估与排序商业智能工具和解决方案
- 准备模糊TOPSIS问卷
- 收集专家关于准则重要性和各备选方案在各项准则下性能的意见，并构建模糊决策矩阵和准则相对重要性矩阵的语言尺度
- 将专家的判断转换为相应的模糊数，并使用算术平均数聚合专家意见
- 归一化模糊决策矩阵并计算加权归一化模糊决策矩阵
- 确定正理想点和负理想点
- 计算各备选方案到正理想点和负理想点的距离
- 计算贴近度系数并对备选方案进行优先排序

第四阶段：比较两种方法，即模糊层次分析法和TOPSIS，并使用斯皮尔曼等级相关检验进行假设检验
- 计算秩的差异和 d² 值。

3. 结果

3.1 关于有效准则及子准则的结果

在本节中，基于研究的实施阶段，并结合用于确定有效标准及子准则的研究问题和研究假设，对这些标准及子准则的假设进行了单独检验。以下示例仅为第一个假设，其他标准及子准则采用相同程序。初始数据通过李克特量表收集，随后使用单样本学生t检验进行研究和分析。

假设1：“技术”作为主要准则对商业智能工具和解决方案的选择具有显著的正向影响。 统计假设包括：
H₀: μ < 3 “技术”对商业智能工具和解决方案选择的影响不高。
H₁: μ ≥ 3 “技术”对商业智能工具和解决方案选择的影响高。

上述假设的问卷数据通过单样本t检验进行统计分析的结果如表6所示。在单样本t检验分析后（假设误差水平为0.05），显著性水平小于0.05且t统计值为正，H₀假设已被拒绝且H₁假设已确认。换句话说，可以以95%的置信度认为，“技术”指数对商业智能工具和解决方案的选择具有重要影响。总之，可以以95%的置信度认为，“技术”指数会影响商业智能工具和解决方案的选型。

表6 假设的单样本t检验结果

指数数量	Mean	T统计量	Sig*	结果
技术	30	4.3333	0.000	假设验证（拒绝H₀）

• α= 0.05

同样，表7显示了针对所有主准则及子准则的假设检验结果。因此，所有选定的准则及子准则均已明确并列入表8，此处提到的相关研究也证实了它们的重要性。

表7 所有主准则和子准则的假设检验结果

准则及子 -准则	Average	Test	高1: μ>3	Sig.
技术	4.33	4.817	已确认	0.00
信息集成	3.8	2.350	已确认	0.026
元数据管理	4.07	3.395	已确认	0.002
存储数据的监控	2.73	-0.724	已拒绝	0.475
来自其他系统的数据录入	2.33	-1.904	已拒绝	0.067
数据仓库	4.07	3.395	已确认	0.002
智能代理	4.07	3.395	已确认	0.002
多代理系统	1.67	-4.817	已拒绝	0.000
可扩展性	2.73	-0.724	已拒绝	0.475
开发的工具	4.47	5.809	已确认	0.000
高级数据分析与交付	4.73	9.355	已确认	0.000
仪表板	4.6	7.180	已确认	0.000
业务分析能力	2.47	-1.490	已拒绝	0.147
移动商业智能	4.33	4.817	已确认	0.000
仪表板功能	2.47	-1.490	已拒绝	0.147
聚类问题	2.07	-2.841	已拒绝	0.008
财务分析工具	1.8	-4.039	已拒绝	0.000
报表工具OLAP	4.6	7.180	已确认	0.000
多准则决策工具	1.8	-4.039	已拒绝	0.000
交互式演示	4.07	3.395	已确认	0.002
现状建模	2.2	-2.350	已拒绝	0.026
灵活性和易用性	3.33	0.360	已拒绝	0.722
仿真模型	1.67	-4.817	已拒绝	0.000
数据挖掘技术	3.53	1.490	已拒绝	0.147
文本挖掘	1.93	-3.395	已拒绝	0.002
向其他系统导出报告	2.73	-0.724	已拒绝	0.475
报告系统	3.8	2.350	已确认	0.026
风险模拟	4.6	7.180	已确认	0.000
公司实力	4.6	7.180	已确认	0.000
安全性	4.73	9.355	已确认	0.000
保留	2.467	-1.490	已拒绝	0.147
市场响应	2.73	-0.724	已拒绝	0.475
供应商经验	4.2	4.039	已确认	0.000
销售策略	2.6	-1.099	已拒绝	0.281
客户评估与预测模型	2.87	-0.36	已拒绝	0.722
供应商的财务稳定性	1.67	-4.817	已拒绝	0.000
与战略供应商的供应商关系	2.46	-1.49	已拒绝	0.147
供应商公司规模	2.33	-1.904	已拒绝	0.067
产品质量	4.73	9.355	已确认	0.000
创新	1.53	-5.809	已拒绝	0.000
全球覆盖和本地存在	2.2	-2.350	已拒绝	0.026
实现目标和承诺的能力	2.6	-1.099	已拒绝	0.281
定制化	2.87	-0.360	已拒绝	0.722
售后服务	2.47	-1.490	已拒绝	0.147
网络咨询	2.6	-1.099	已拒绝	0.281
实施所需时间	3.93	2.841	已确认	0.008
保修	1.93	-3.395	已拒绝	0.002
产品价格	4.47	5.809	已确认	0.000
供应商和教育合作伙伴	2.6	-1.099	已拒绝	0.281
学习技巧	2.067	-0.724	已拒绝	0.475
组织访问	2.067	-2.841	已拒绝	0.008
组织整合	1.93	-3.395	已拒绝	0.002

| 组织稳定性 | 2.73 | -0.724 | 已拒绝 | 0.475 |
| 合同管理 | 2.07 | -2.841 | 已拒绝 | 0.008 |
| 各部门的渗透率 | 1.53 | -5.809 | 已拒绝 | 0.000 |

表8 选定的标准及其参考文献

Row	标准和子项 ‐ 标准	研究
1	技术	鲍尔（2007）、维尔切利斯（2009）、斯特尔和雷诺兹（2011）、SAS研究所公司（2004）、威廉姆斯和威廉姆斯（2007）
	元数据管理	钱成（2007）、维尔切利斯（2009）、莫斯和阿特雷（2003）、兰詹（2009）。
	数据仓库	谭等（2003）、维尔切利斯（2009）、金博尔等（1998）、戴奇（2000）、因蒙（2002）、金博尔和罗斯（2002）、内马提等人 等（2002），
	智能代理	高和徐（2009）、李等人（2009）、鲁哈尼、加赞法里和贾法里（2012）
	开发的工具	史等人（2007）、高和徐（2009）
	信息集成	赫歇尔和琼斯（2005）、博洛朱、哈利法和特班（2002）、内马提等人（2002）、马龙、克罗斯顿和赫尔曼（2003），希帕蒂亚研究（2009），唐纳德和华纳（2007），萨巴诺维奇（2008），
2	高级数据分析 和交付	鲍尔（2007），韦尔切利斯（2009），库珀等人（2000），萨纳苏利斯（2001），莫斯和阿特雷（2003），奈穆扎曼（2009），唐纳德和华纳（2007）
	仪表板	内马提等人（2002）、黑奇贝思（2007）、博斯（2009）、沃伦等 (2011)、Stackowiak 等 (2007)、鲁哈尼等（2012）
	报告系统	韦尔切利斯（2009）、斯特尔和雷诺兹（2011）、希帕蒂亚研究（2009）、奈穆扎曼（2009）、唐纳德和华纳（2007）
	移动商业智能	拜耳等（2011）、斯蒂皮奇和布龙津（2011）、本斯伯格（2008）、朱和黄（2012）、斯特尔和雷诺兹（2011）、阿伊丁和哈里洛夫 (2012)
	OLAP	谭等（2003），刘等（2004），里维斯特等（2005），史等人（2007），贝尔萨尔等（2008），李等人（2009），兰詹 （2009），鲁哈尼等（2012），韦尔切利斯（2009），
	交互式演示	什穆埃利等 (2010)，兰詹（2009），萨巴诺维奇（2008），鲁哈尼等（2012）
	数据挖掘技术	博洛朱、哈利法和特班（2002），史等人（2007），贝尔萨尔、库贝罗和希门尼斯（2008），程、卢和邵（2009），特弗季科娃 (2007)，维尔切利斯（2009），哈斯蒂等 (2001)，韩和坎伯 (2005)，哈斯蒂等 (2001)，派尔（2003）。
	风险模拟	埃弗斯 (2008)，加拉索和蒂埃里 (2008)，鲍尔（2007），鲁哈尼、加赞法里和贾法里（2012）
	灵活性和易用性	赖希和卡佩留克 (2005)，扎克 (2007)，林等 (2009)，韦尔切利斯（2009），SAS研究所公司（2004），伊西克(2010)，豪森。(2008)，阿巴尔特伊诺娃和威廉姆斯(2009)。
3	公司实力	SAS研究所公司（2004）
	安全性	沃伦等 (2011)，阿伊丁和哈里洛夫 (2012)，希帕蒂亚研究（2009），\ 英霍夫 (2010)，袁和刘 (2008)
	供应商经验	Shmueli 等 (2010)，威廉姆斯和威廉姆斯（2007），唐纳德和华纳（2007），Kumar 等 (2009)，阿马拉，Y. 等 (2008)
	产品质量	韦尔切利斯（2009），Sanjay Kumar 等 (2009)，Bross 和 Zhao (2004)，Amara 等 (2008)
	支持服务	Shmueli、Patel 和 Bruce (2010)，Macgllivray (2000)
	实施所需时间 实施	斯特尔和雷诺兹（2011），Kumar 等 (2009)，Yuen 和 Lau (2008)，Amara 等 (2008)，Naimuzzaman(2009)
	产品价格	韦尔切利斯（2009），Stackowiak 等 (2007)，Imhoff,(2010)，Kumar 等 (2009)，Adelakun 和 Kemper (2010)，Amara 等 (2008)

3.2 模糊AHP方法实施结果

步骤1：通过确定标准、子准则和备选方案获得层次结构

如前所述，影响商业智能工具排序的准则及子准则包括3个主准则、19个子准则和6个备选方案，这些是通过文献回顾、获取专家意见以及假设检验后确定的。在确定准则及子准则之后，已构建了本研究的概念模型及其用于对商业智能工具和供应商进行排序的层次结构，如图3所示。表9展示了包含目标、准则及子准则及其编码的三层层次结构。

表9 标准、子准则和备选方案的层级及其代码

第一级 目标	准则代码	第二层级（标准）	Sub- 标准 code	第三级（子准则）	第四级 （备选方案）备选 编方案 码
	C1	技术	C11	信息集成
			C12	数据仓库
			C13	元数据管理
			C14	智能代理
			C15	开发的工具
	C2	高级数据分析与交付	C21	仪表板	IBM Alt 1
			C22	数据挖掘技术	微软 Alt 2
			C23	OLAP	SAP Alt 3
			C24	移动商业智能	QlikTech Alt 4
			C25	风险模拟	SAS Alt 5
			C26	视觉交互	甲骨文 Alt 6
			C27	灵活性和易用性
			C28	报告系统
	C3	公司实力	C31	安全性
			C32	供应商经验
			C33	产品质量
			C34	产品价格
			C35	实施所需时间
			C36	支持服务

表10 第二层级（标准）两两比较的专家意见聚合矩阵

标准	C1	C2	C3
C1	(1, 1, 1)	(1, 1.346, 1.601)	(1.739, 2.284, 2.779)
C2	(0.624, 0.743, 1)	(1, 1, 1)	(1.511, 2.119, 2.643)
C3	(0.36, 0.438, 0.575)	(0.378, 0.472, 0.662)	(1, 1, 1)

步骤3：计算一致性比率

为了检验关于表10所示的第一对比较矩阵的专家意见聚合的一致性，构建了中间数矩阵，并使用公式(6)、公式(7)和公式(29)计算最大特征值λmax。

(29)
det(A - λI) = 0

使用公式29，表10中中间数矩阵的最大特征值为0.053；因此：

CI = (λmax - n) / (n - 1) = (3.0055 - 3) / (3 - 1) = 0.0027
CR = CI / RI = 0.0027 / 0.58 = 0.0053 < 0.1

因此，我们得出结论：第一对比较矩阵的聚合意见是一致的。

步骤4：使用CFCS方法计算专家意见聚合矩阵的清晰矩阵

如前所述，在确保意见的一致性后，必须将成对比较矩阵从模糊尺度转换为清晰尺度，这称为模糊对比较矩阵的去模糊化。在本研究中，使用公式8到15对专家的模糊答案进行去模糊化。表11显示了表10中数值的去模糊化结果。

表11 数值的去模糊化的结果准则

C1	C2	C3
1	1.331604	2.237736
0.772016	1	2.071574
0.445693	0.486281	1

步骤5：计算最终权重

最后，在计算出意见的非模糊值后，使用公式16来获得权重。表12显示了这些权重。

表12 聚合意见的清晰矩阵及标准的最终重量

标准	C1	C2	C3	权重
C1	1	1.331604	2.237736	0.4484
C2	0.772016	1	2.071574	0.3644
C3	0.445693	0.486281	1	0.1872

如图和表10所示，准则的重要性的顺序包括技术、高级数据分析与交付以及公司实力。结果表明，技术是最重要的优先级，其次是报告形式的高级数据分析与交付，然后是供应商和软件公司的实力。

类似地，针对每个准则下三组子准则的成对比较矩阵进行了聚合，检查了一致性，转换为非模糊数，并最终计算了它们的最终权重（表13、表14和表15）。

表13 聚合意见的清晰矩阵及与技术准则相关的子准则最终权重 (CR= 0.065)

子准则	C11	C12	C13	C14	C15	权重
C11	1	2.244235	3.039771	1.374425	2.264451	0.3399
C12	0.451642	1	2.824802	1.76802	1.73072	0.2423
C13	0.326099	0.351546	1	1.749658	1.407403	0.1433
C14	0.750222	0.582825	0.582664	1	1.092141	0.1428
C15	0.444418	0.590252	0.733906	0.963247	1	0.1317

表14 聚合意见的清晰矩阵及与高级数据分析与交付准则相关的子准则最终权重 (CR= 0.0743)

子准则	C21	C22	C23	C24	C25	C26	C27	C28	权重
C21	1	0.571655	1.137106	3.789024	1.836886	1.552565	0.68986	0.690194	0.1328
C22	1.780132	1	0.999155	3.068386	3.05151	2.223608	1.015652	0.753311	0.1734
C23	0.89823	1.012053	1	5.435926	3.336901	4.239199	1.266887	1.611174	0.2123
C24	0.262498	0.328682	0.180317	1	0.63691	0.587145	0.562166	0.504602	0.0513
C25	0.553091	0.327953	0.30052	1.60229	1	1.520171	1.928036	1.764895	0.1034
C26	0.65155	0.458945	0.234944	1.736325	0.677518	1	0.480499	0.742465	0.0735
C27	1.475219	1.015652	0.802638	1.807685	0.526787	2.105711	1	1.506898	0.1342
C28	1.49878	1.361965	0.639068	2.007673	0.573144	1.385969	0.680728	1	0.1193

表15 公司实力准则相关子准则的聚合意见的清晰矩阵及最终权重（= 0.0911）

子准则	C31	C32	C33	C34	C35	C36	权重
C31	1	1.321258	0.807933	1.38186	1.611507	1.904419	0.2045
C32	0.770393	1	1.131916	1.915559	1.056762	1.960722	0.1956
C33	1.268738	0.89706	1	3.642385	3.436424	0.731684	0.2350
C34	0.733586	0.529496	0.269417	1	1.751069	1.579013	0.1293
C35	0.627758	0.9587	0.288345	0.595287	1	1.171978	0.1118
C36	0.541602	0.511301	1.406662	0.65597	0.872441	1	0.1238

为了完成对备选方案进行排序所需的剩余两两比较，应将研究中的19个子准则和6个备选方案进行两两比较。表16总结了根据每个子准则得出的备选方案权重的全部结果。

表16 备选方案关于问题子准则的权重矩阵

备选方案	C11	C12	C13	C14	C15	C21	C22	C23	C24	C25	C26	C27	C28	C31	C32	C33	C34	C35	C36
IBM	0.2052	0.2778	0.289360016	0.294553044	0.1913	0.1572	0.2919	0.4354	0.1716	0.2524	0.2216	0.0983	0.1279	0.1767	0.2418	0.3078	0.1592	0.1583	0.1113
Microsoft	0.1025	0.1019	0.101980727	0.075183013	0.0904	0.0803	0.0851	0.0812	0.0969	0.0924	0.0867	0.1255	0.0737	0.0827	0.0722	0.1089	0.337	0.2201	0.0978
SAP	0.2074	0.1317	0.135184305	0.137521416	0.105	0.1838	0.104	0.1354	0.1572	0.1367	0.1144	0.1485	0.1046	0.1447	0.0903	0.0932	0.1121	0.0702	0.1741
QlikTech	0.1225	0.0843	0.157577753	0.148196589	0.1896	0.2107	0.1597	0.1054	0.1996	0.1723	0.1913	0.3304	0.225	0.1892	0.1272	0.1213	0.1199	0.224	0.1622
SAS	0.1206	0.1509	0.124165084	0.180860982	0.2183	0.1738	0.2037	0.1389	0.2232	0.1945	0.2345	0.2045	0.2692	0.1552	0.2551	0.1795	0.1386	0.1833	0.1983
Oracle	0.2417	0.2534	0.191732114	0.163684956	0.2054	0.1941	0.1557	0.1037	0.1516	0.1517	0.1515	0.0929	0.1996	0.2514	0.2134	0.1894	0.1332	0.144	0.2563

为了更好地理解各备选方案在每个子准则上的两两比较结果，图5展示了表16的结果，并显示了每个备选方案在各子准则上的性能。然而，对于备选方案权重的最终计算，除了表17中给出的重要性值矩阵外，还需要子准则的最终权重矩阵。这些矩阵可通过将每个标准的权重乘以其相应的子准则得到。例如，在表17中，我们有 0.448 × 0.3399 = 0.1524。

通过将表16（一个6×19矩阵）进行矩阵乘法运算154如表17所示的子准则最终权重矩阵为1×19矩阵，由此得到备选方案的最终1×6权重矩阵。图6显示了备选方案的最终重量。

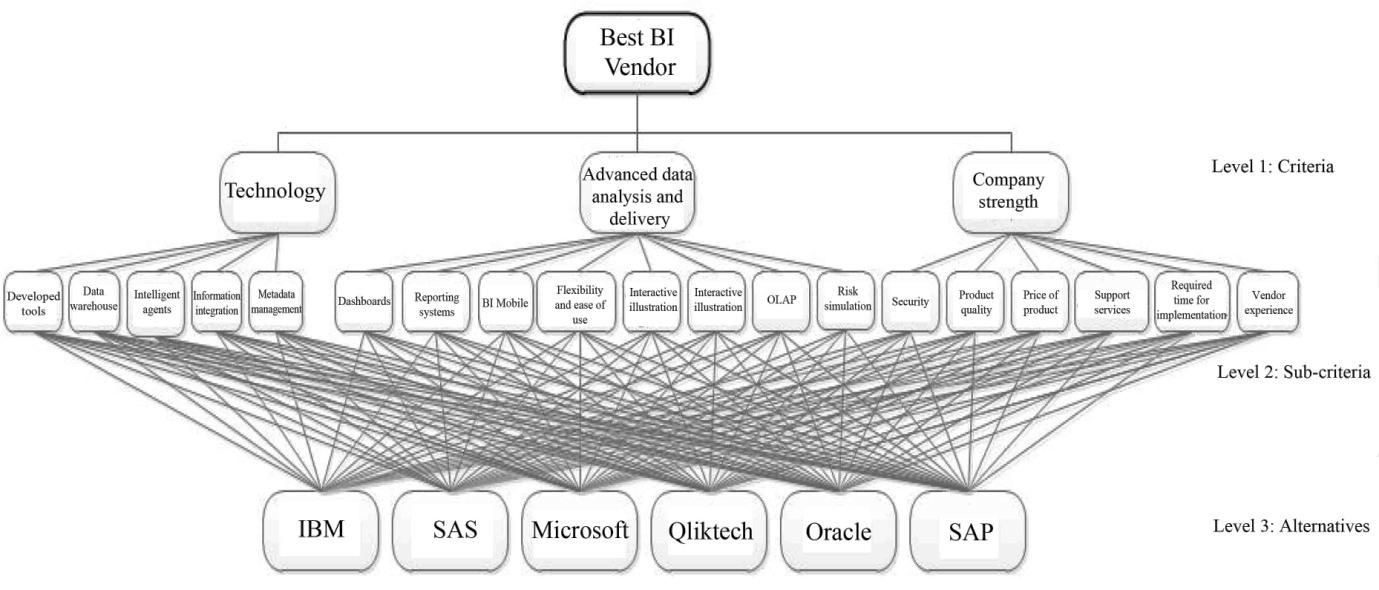
表17 子准则最终权重

Criteria code	标准	准则权重	子准则 code	子准则	子准则局部权重	子准则最终权重	最终重量的准则
C1	技术	0.448	C11	信息集成	0.3399	0.1524	1
			C12	数据仓库	0.2423	0.1086	2
			C13	元数据管理	0.1433	0.0642	4
			C14	智能代理	0.1428	0.0641	5
			C15	开发的工具	0.1317	0.0591	7
C2	高级数据分析和交付	0.364	C21	仪表板	0.1328	0.0484	9
			C22	数据挖掘技术	0.1734	0.0632	6
			C23	OLAP	0.2123	0.0773	3
			C24	移动商业智能	0.0513	0.0187	19
			C25	风险模拟	0.1034	0.0377	13
			C26	视觉交互	0.0735	0.0268	15
			C27	灵活性和易用性	0.1342	0.0489	8
			C28	报告系统	0.1193	0.0435	11
C3	公司实力	0.187	C31	安全性	0.2045	0.0383	12
			C32	供应商经验	0.1956	0.0366	14
			C33	产品质量	0.2350	0.0440	10
			C34	产品价格	0.1293	0.0242	16
			C35	实施所需时间	0.1118	0.0209	18
			C36	支持服务	0.1238	0.0232	17

模糊AHP方法的最终结果中，各备选方案的最终权重和排名如表18所示。

表18 备选方案的最终权重和排名

备选方案	最终权重	Rank
IBM	0.2378	1
甲骨文	0.1903	2
SAS	0.1737	3
QlikTech	0.1569	4
SAP	0.1396	5
微软	0.1016	6

排序结果表明，IBM 是该组织的首选，这归因于其在几乎所有准则及子准则方面的优势。紧随其后的是甲骨文、SAS、QlikTech、SAP 和微软，如表19所示。

表19 基于排名的公司比较

公司	本研究中的排名	世界排名
IBM	1	1
甲骨文	2	7
SAS	3	2
QlikTech	4	9
SAP	5	8
微软	6	5

事实上，在包括IBM、甲骨文、SAP和微软在内的商业智能超大型供应商中，除了IBM和甲骨文分别排名第一和第二外，其他超大型供应商如SAP和微软则分别排名第五和第六。根据高德纳（Desisto, 2012）的分类，QlikTech和SAS属于商业智能市场中的独立供应商，分别位列第四和第五。

3.3 模糊TOPSIS方法的实施结果

如前所述，为了评估商业智能供应商的标准、子准则及备选方案，采用了模糊TOPSIS方法，具体步骤如下。

步骤1：根据语言尺度构建模糊决策矩阵和准则相对重要性矩阵

使用模糊TOPSIS问卷以及表20和表21中提供的量表，专家被要求评估各子准则的重要性的顺序以及备选方案在每个子准则下的性能。表20显示了专家对子准则重要性的意见。通过将每位专家的判断转换为模糊数并进行平均，可确定意见均值。专家对子准则重要性意见的平均值见表20，而“技术”五个子准则针对备选方案的意见均值见表21。

表 20 七位专家对子准则重要性的意见

Questionnaire 1	Questionnaire 2	Questionnaire 3	Questionnaire 4	Questionnaire 5	Questionnaire 6	Questionnaire 7
C11 H MH H H VH VH H	C12 MH H VH MH H MH VH	C13 MH H H MH VH VH VH	C14 H H H H MH VH H	C15 H H MH M VH MH VH	C21 VH MH H H VH H VH	C22 MH VH H MH H VH H
C23 VH VH H M MH H MH	C24 M MH H M MH H H	C25 M MH H M MH M MH	C26 ML H H MH MH VH VH	C27 H H H ML VH H VH	C28 H H H MH VH MH H	C31 VH MH VH ML MH MH VH
C32 MH M H M VH VH MH	C33 H MH VH M VH VH H	C34 MH M H M H H H	C35 MH MH H MH VH H VH	C36 H MH VH H VH VH H

表21 专家对子准则重要性意见的平均值

Alternatives 重要性均值 ce
C11	0.729	0.9 0.986
C12	0.671	0.843 0.957
C13	0.729	0.886 0.971
C14	0.7	0.886 0.986
C15	0.643	0.814 0.929
C21	0.757	0.914 0.986
C22	0.7	0.871 0.971
C23	0.643	0.814 0.929
C24	0.529	0.729 0.886
C25	0.443	0.643 0.829
C26	0.614	0.786 0.9
C27	0.671	0.843 0.929
C28	0.671	0.857 0.971
C31	0.614	0.771 0.886
C32	0.586	0.757 0.886
C33	0.7	0.857 0.943
C34	0.557	0.757 0.9
C35	0.671	0.843 0.957
C36	0.757	0.914 0.986

步骤2：模糊决策矩阵归一化和计算加权归一化模糊决策矩阵

需要注意的是，在本研究中，所有子准则均被视为正向标准，例如