哨兵：智能车辆变道建议系统

哨兵：一种用于智能车辆的车载车道变换建议系统，以减少高速公路事故期间的交通延误

摘要

本文介绍了哨兵（Sentinel），一种用于智能车辆的车载系统，可在高速公路事故发生时引导车辆的变道行为，旨在减少交通拥堵、通行能力下降和延误。当检测到前方车道发生封闭车道的事故时，哨兵在每个时间步长计算车辆在到达事故点之前离开封闭车道的概率。当该概率随着车辆接近拥堵边界而降至某一阈值以下时，哨兵将建议车辆离开封闭车道。通过这种方式，哨兵减少了封闭车道内车辆在临近事故点时进行后期阶段车道变换的数量，并将这些操作分布到事故点上游。本研究开展了一项仿真实例研究，模拟美国I‐66州际公路一段四车道中一条车道因事故被临时封闭的情形，以了解哨兵对交通流的影响，以及不同参数——交通流、系统渗透率和事故持续时间——如何影响哨兵的性能。结果表明，哨兵对交通流具有积极影响，可使平均延误最多减少37%，尤其是在其渗透率达到较高水平时效果更为显著。哨兵与交通事件管理系统（TIMS）协同工作，有望成为减少交通延误的重要工具，并可能每年为因高速公路事故引发的拥堵所造成的经济损失节省数十亿美元。

关键词 —高速公路事故，智能车辆，换道，概率模型，交通仿真。

一、引言

FREEWAY 拥堵可分为两类：常发性拥堵和非经常性拥堵。常发性拥堵主要是由于交通流超过道路容量，在固定位置形成交通瓶颈所致，例如车道减少处。相比之下，非经常性拥堵通常由高速公路事故（交通事故、车辆故障等）或计划内的特殊事件（高速公路维护、施工等）引起[1]。

美国德克萨斯交通研究所基于2017年数据发布的2019年城市移动性报告发现，由于累计达88亿小时的浪费时间和33亿加仑的浪费燃料，拥堵每年给美国造成约1660亿美元的拥堵成本[2]。全国交通事件管理联盟（NTIMC）估计，交通事件占美国道路总延误的约25%[3]。因此，在高速公路事故期间对交通流进行任何小幅改善，都可以节省大量时间和资金，而智能车辆的出现为这一领域带来了新的机遇。

为了减轻非经常性拥堵（尤其是高速公路事故）对交通流的影响，美国各地的州和地方政府传统上依赖交通事件管理系统（TIMS）。TIMS的目标是准确预测交通事件的发生，并缩短事件的检测、响应和清除时间[4]。该领域的研究人员已对这些方面进行了广泛研究。

增强的事件预测使交通事件管理系统（TIMS）能够通过更高效地分配资源来更好地应对事件，从而实现更快的响应并减少延误。该领域的以往研究探讨了使用基于参数树的模型（CART或分类与回归树）、人工神经网络以及负二项回归模型进行事故频率预测[5],[6]。以往的研究还研究了使用随机效应probit模型来预测高速公路事故发生可能性[7]；利用环路数据通过图解特征向量进行实时碰撞可能性预测[8]；以及使用Hadoop框架高效处理和分析大型交通数据以进行事故预测[9]。类似地，具备低误报率的交通事件自动、快速、准确检测能力，可使交通事件管理系统（TIMS）更快响应，并减少总体延误。

该领域以往的研究已采用模糊小波径向基函数神经网络[10],[11],、构造性概率神经网络（CPNN）[12],[13],、小波变换技术[14],以及小波‐聚类‐神经网络[1]进行高速公路事件检测，提出了具有高准确性且误报率低、能够适应不同交通状况的事件检测方法。

准确估计事件持续时间还有助于交通事件管理系统（TIMS）更高效地制定应对和清除事件的决策，从而减少事件对交通流的潜在影响。该领域的以往研究应用了基于风险的持续时间模型，用于统计评估检测/报告、响应和清除事件所需的时间[15],，并采用生存分析方法开发了加速失效时间预测模型[16]。此外，还研究了一种特征选择方法采用遗传算法构建基于人工神经网络的模型，以对事故持续时间进行序列预测[17],，并针对不同类型的事件开发了事件持续时间模型，研究了影响事故持续时间的多个变量[18]。最近的研究进一步提出了用于事故持续时间预测的新型M5P‐HBDM模型[19]，以及利用梯度提升决策树（GBDTs）基于不同类型的解释变量预测非线性和不平衡事件清除时间的方法[20]。此外，还提出了基于Copula的建模框架，用于理解影响因素对事件检测、响应和清除时间的影响[21]，以及一种数据驱动方法，用于自动确定高速公路事故的时空影响区域[22]。总体而言，这些研究加深了我们对影响事件持续时间参数的理解，并提高了估计事件检测、响应和清除所需时间的准确性。

TIMS的最后一环是寻找在响应并清除道路上的事件所需时间内，对事件发生地点上游交通进行管理的方法。为此，TIMS依赖于为管理道路瓶颈处常发性拥堵而开发的方法[23],，包括采用可变限速（VSL）策略[24]–[26],、拥堵辅助系统[27]–[30],，或两者结合使用[31],[32]。所提出的VSL策略通常涉及通过各种优化方法和控制算法动态调整瓶颈上游的限速。宏观仿真表明，这些方法在减少总行程时间（TTT）和防止通行能力下降方面是有效的[26]；但如[31]所指出的，在微观仿真中，由于缺乏车道分配策略，这些方法可能会失效，因为延误和通行能力下降通常是由于接近瓶颈处的紧急变道引起的。

即使存在车道分配策略，部署上述交通管理方法仍依赖于道路基础设施（例如overhead龙门架），而这些设施仅在大型城市地区附近可用，这限制了它们应对随机性交通事件的有效性。为解决这一问题，我们的研究利用了联网、自动驾驶和ADAS赋能车辆（下统称为智能车辆）的出现及其潜力[33]。为此，我们提出了哨兵，这是一种用于智能车辆的车载系统，利用概率预测模型[34]–[36]来引导车辆在高速公路事故期间的变道行为。该方法不仅通过减少高速公路事故期间的交通延误节省了大量的时间和成本，而且通过改善交通流、降低引发二次事件的可能性[20]，促进了交通事件管理系统更快响应并加快道路清障。此外，哨兵仅依赖车辆自身的车载感知能力，无需任何外部道路基础设施，尽管其性能可通过利用车联网技术得到提升。

本文其余部分组织如下。第二节介绍了方法论，包括哨兵系统背后概率模型的简要概述、哨兵系统的工作原理以及用于评估其性能的仿真设置。第三节展示了结果，并讨论了哨兵系统对交通流和效率的影响。最后，第四节总结了本文的主要发现，并提出了未来研究方向。

II. 方法论

在进行方法论之前，我们首先需要定义一些术语。在整个研究工作（包括上一节）中，道路上上游流量容量高于下游流量容量的点被称为瓶颈[28]。瓶颈可能是由道路特征（如合流区和车道减少）或由事件或道路维护引起的临时车道封闭所导致的。此外，如第I节所述，智能车辆被定义为能够实现SAE二级自动驾驶[37]的车辆。换句话说，该车辆配备有一个或多个环境感知传感器（雷达、摄像头等），以支持其高级驾驶辅助系统（ADAS）。

瓶颈的名义容量定义为在瓶颈点上下游能够同时维持的最大交通流量。换句话说，如果C表示道路从m条车道过渡到n条车道处瓶颈点的上游通行能力，m>n，则名义瓶颈容量Cb定义为 n mC。然而，实际瓶颈容量通常低于名义容量Cb，原因可能是上游交通流量超过Cb，或封闭车道上的车辆进行仓促的换道操作，干扰交通流并降低其他车辆的速度。这种通行能力的下降称为通行能力下降，以往研究表明，实际瓶颈容量可能比名义容量低5%到20%[38],[39]。通行能力下降会扰乱交通流，并导致所有车辆的延误增加。

如第一节所述，“哨兵”是一种车载系统，利用感知数据、事故位置信息以及预测模型，估算通过一次或多次车道变换到达道路目标点的可能性，旨在减少交通延误并推迟或防止高速公路事故发生时的通行能力下降。当检测到前方车道被封闭时，“哨兵”会在每个时间步长计算在到达事故点之前离开封闭车道的概率。当该概率降至某一阈值以下时，即车辆接近拥堵边界时，“哨兵”会建议车辆进行换道。通过这种方式，“哨兵”减少了封闭车道内车辆在临近事故点时进行后期阶段车道变换的次数，并将这些换道操作分布在事故点上游区域。关于“哨兵”运行机制的详细描述见第二节‐B，实现相关细节见第二节‐B.3。

哨兵在VISSIM®中实现了对I‐66州际公路一段四车道区域的系列仿真，其中最右侧车道被封锁了一定时间。接下来，第二节‐A简要概述了上述概率预测模型，而第二节‐B描述了哨兵的运行和实现

A. 概率模型

[34]中引入的模型用于估计车辆通过一次或多次变道到达短期目标状态的概率。尽管详细的模型推导和验证可在[34],中找到，但此处提供了该模型的简要概述，以帮助读者熟悉相关内容。

考虑一条有n条车道的道路，车道从左到右编号为1到n。不妨假设自车希望到达车道n上距离其在车道1的当前位置前方d处的位置，并令P(S)表示成功实现该目标的概率。该模型通过一些假设来估计此概率。首先，假设车道i（1≤i≤n）上所有车辆的速度均等于vi，其中vi可视为该车道上所有车辆在一段时间内的平均速度。其次，假设车道i上的车间距是来自由参数μi和σi[40]定义的共同对数正态分布的独立同分布随机变量。最后，假设自车在换道时遵循吉普斯间隙接受模型[41]。也就是说，如果自车位于车道i−1，仅当相邻车道i上前导和后随车辆之间的间隙不小于最小可接受（临界）间隙gi时，才执行换道操作。该换道操作在ti秒内完成。图1展示了其中部分假设，以便更直观地理解。

该模型根据上述定义的参数计算P(S)。换句话说，对于上述情况，P(S)=fn(d,v1:n,μ2:n,σ2:n,g2:n,t2:n)，其中qa:b表示参数q及其下标b≥a对应的qa,qa+1,…,qb。P(S)通过以n=2为基准情况的归纳法得到。在基准情况下，由于P(S)没有闭式表达式，因此通过查找表获得（作为三个参数的函数），该查找表的值是利用蒙特卡洛仿真对问题[34],[42]进行计算得出的。对于n>2的情况，P(S)通过递归方式确定。

f n(d, v1:n,μ2:n, σ2:n, g2:n, t2:n)
= ∫ d
0
f 2(d −x, vn−1:n,μ n, σ n, gn, tn) × ∂ ∂x f n−1(x, v1:n−1,μ 2:n−1, σ 2:n−1, g2:n−1, t2:n−1)dx = ∂ ∂x ∫
d
0
f 2(d −x, v n−1:n ,μ n , σ n , gn , tn)
×f n− 1(x, v 1:n− 1 ,μ 2:n− 1 , σ 2:n− 1 , g2:n− 1 , t2:n− 1)dx ,(1)
基于全概率定律[43]。针对一系列参数进行的大量交通仿真证实，在大多数情况下，该模型的准确度在实际概率的4%以内。仿真还验证了我们的观察结果：总体而言，当与目标状态的距离减小（d增大）、相邻车道的交通密度增加（μi增大）或驾驶员行为较为保守（gi增大）时，概率会下降。

B. 仿真设置

哨兵利用概率模型来引导智能车辆的变道行为，旨在达到特定的目标状态，即应对由高速公路事故引起的拥堵。具体而言，当配备哨兵的车辆接近高速公路事故并处于封闭车道时，哨兵利用对事故发生位置的了解来计算d，并利用感知和车辆数据来计算vi,μi和σi。结合驾驶员或自动驾驶车辆调优参数gi和ti，在每个时间步长，哨兵会估算该车辆在到达事故点前，在这些条件下通过一次或多次车道变换驶出封闭车道的概率。当该概率降至某一阈值pl以下时，哨兵将指示车辆进行换道。通过这种方法，哨兵减少了封闭车道内车辆在后期阶段为进入其他车道而进行的扰乱交通的车道变换，并将这些操作分布到事故点上游。换句话说，哨兵的目标是通过改变单车辆的行为来减少拥堵。

准确掌握事件信息对于哨兵系统的运行至关重要，因为需要这些信息来计算d并判断车辆是否位于封闭车道上。该信息可通过多种不同来源获取。一种来源是交通事件管理系统（TIMS），如第I节所述，TIMS可通过多种方法[1],[10]–[14]检测事件。除了事件位置外，TIMS通常还能通过观察事件下游车辆的放行率推断出封闭车道数，但无法确定具体哪些车道被封闭。第二种信息来源是在线导航服务（如Waze和谷歌地图）提供的众包事故及车道封闭数据。这些服务目前已允许用户报告交通事件的位置，未来可能还支持用户指明事件所影响的具体封闭车道。最后一种获取事件信息的方式是车与车（V2V）通信连接。

通过这种技术，经过事件现场的车辆可以将其位置以及事件所阻塞的具体车道信息传递给上游配备车对车通信技术的车辆。智能车辆可以获取并整合这三个来源中的部分或全部信息，以确定事件的位置及其阻塞的车道[30]。

哨兵还需要获取智能车辆周围交通的信息，以估计诸如vi,μi和σi等参数的值。这些信息的主要来源是车辆自身的感知传感器。大多数（如果不是全部）智能车辆都配备了若干雷达和摄像头传感器，以实现车道保持、自适应巡航控制（ACC）和紧急制动等高级驾驶辅助系统（ADAS），满足SAE二级自动驾驶的要求。哨兵可以利用这些传感器的观测数据来确定周围车辆的速度及其车间距，从而估算出vi,μi和σi。当然，如果车辆配备了车联网技术，则可以利用车对车通信（V2V通信）获得关于周围车辆速度及其车间距的更准确信息。

与其他高级驾驶辅助系统一样，驾驶员合规性对于哨兵系统的成功运行至关重要。在本案例中，不合规车辆是指未按照哨兵系统建议进行变道的车辆，因此这些车辆在实际中与未配备哨兵系统的车辆几乎无法区分。因此，在本文中我们假设配备哨兵系统的车辆均完全合规，并将不合规车辆和未配备哨兵系统的车辆视为相同。

使用VISSIM®交通仿真来研究“哨兵”在高速公路事故期间对交通流、道路通行能力和平均延误的影响。通过改变事故持续时间、交通流以及“哨兵”渗透率，针对多种交通状况进行了仿真实验。对于每种情况，我们研究了不同的概率阈值pl（“哨兵”建议车辆驶离封闭车道的临界值）如何影响道路通行能力、平均延误和整体交通流。

第II‐B.1节至第II‐B.4节详细讨论了仿真设置。

1) 仿真基础

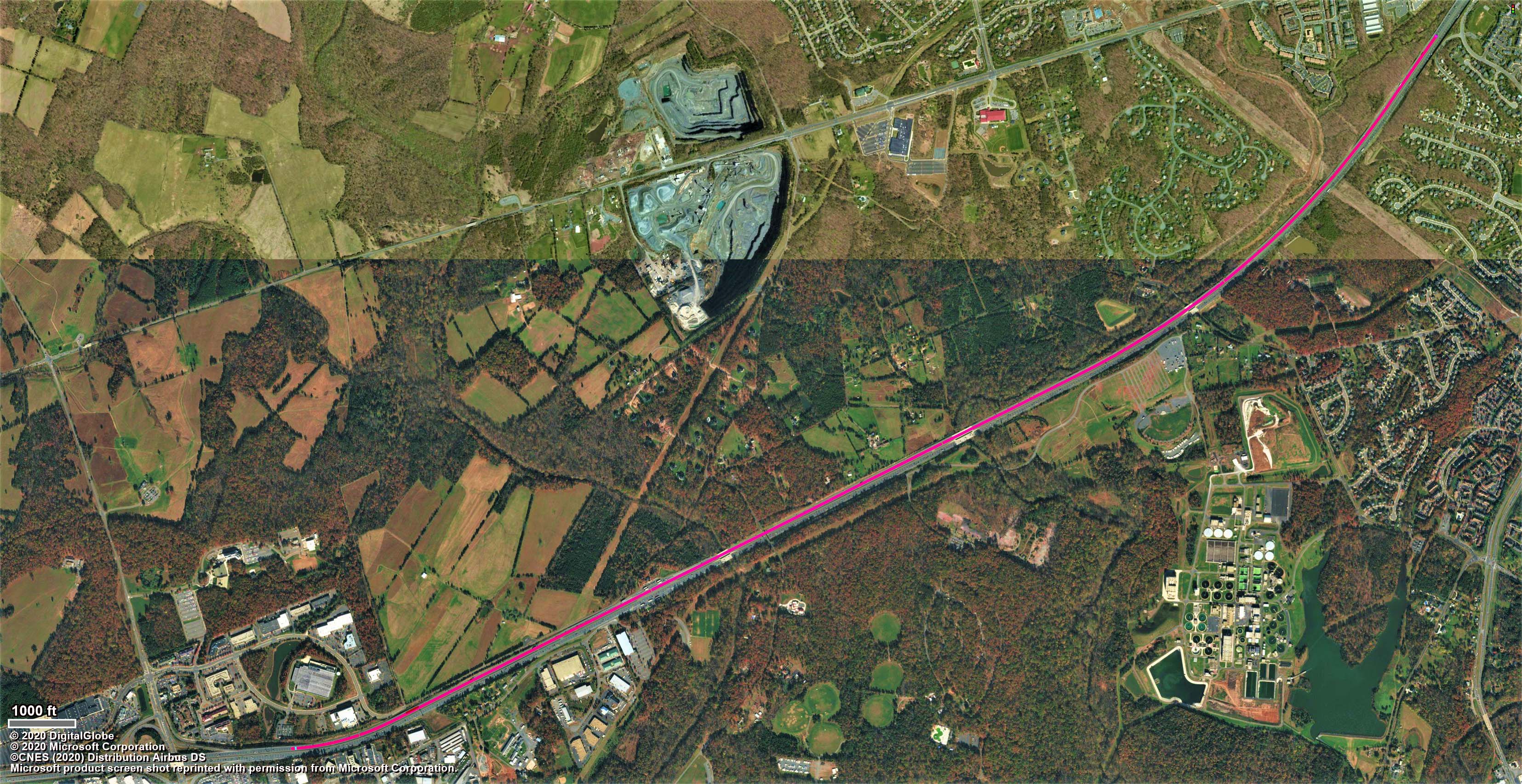
我们选择华盛顿特区郊区西行I‐66州际高速公路的一段作为仿真实验路段。如图2所示，该路段为四车道，全长21,054英尺（3.99英里）。起点位于李公路合流处加速车道结束之后，终点位于通往萨德利路出口匝道的减速车道之前。整个道路段被模拟为单一路段，并在起点处设置车辆输入。

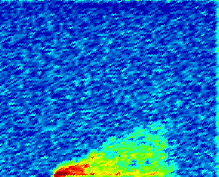
根据弗吉尼亚州交通部（VDOT）《交通运行与安全分析手册》（TOSAM）以及VDOT VISSIM®用户指南[44],[45]进行了交通仿真。建议对每个仿真案例使用不同但一致的随机种子运行10次，并对结果进行平均。然而，我们发现某些案例中，少数仿真运行在完成前发生崩溃，1因此我们将每个仿真案例运行12次，2开始

1在几次运行中，当“哨兵”建议车辆变道时，VISSIM®控制车辆驾驶行为的内部模型计算出的轨迹角度大于90度，导致发生碰撞。2该数值受限于可用内存容量。

从随机种子42开始，后续运行每次递增5。每次仿真运行持续9000秒，其中前1800秒为播种期，其余时间为分析期[45]。

基于三个参数的不同组合，研究了多种仿真案例：输入车流量qi、哨兵渗透率r和事故持续时间γi。qi设置为6400、7200或8000辆/小时，r设置为10%、40%或70%，γi设置为30分钟或60分钟。在可能的18种情况中，有三种未进行研究，即当γi=60分钟且qi=8000辆/小时时，因为由此产生的拥堵会超出输入范围。

每次仿真中使用的北美车辆3包含四种不同类型的车辆：汽车、配备Sentinel的（SE）轿车、公交车（事件建模所需）以及重型货车（HGVs）。SE车辆与普通汽车完全相同，唯一的区别在于控制其换道发起行为的外部驾驶人模型（EDM），用于模拟现实生活中配备Sentinel的车辆（详见第二节‐B.3）。SE车辆、普通汽车、重型货车和公交车的车辆组成按r设置如下：r，85%‐r，13%和2%。例如，如果r=70%，则SE车辆、普通汽车、重型货车和公交车的比例分别设为70%、15%、13%和2%。所有车辆的期望速度分布在输入时设定为70英里/小时，每辆车被随机分配一个介于67英里/小时到80英里/小时之间的期望速度，且采用均匀概率[44]。最后，定义了一组行程时间测量方法，用于测量整个仿真过程中的总行程时间（TTTs）和延误情况。行程时间从道路段起点开始测量至接近终点处，覆盖总距离为21,000英尺。

使用VISSIM®的公共交通功能来模拟高速公路事故。具体而言，在19,000英尺处的最右侧车道上定义了一个公交站，总长度为200英尺。在每次仿真中，一辆公交车会在3600秒时驶入并在该站点停车，从而有效阻塞该车道的交通。公交车将在5400秒或7200秒时离开站点，以此模拟总事件时间γi分别为30分钟或60分钟的事故情况。

2) 驾驶行为

根据[44],[45]，采用先前弗吉尼亚州交通部研究[46]的数据来定义单一路段的驾驶行为。由于预计事故将引发显著的交织与合流行为，因此采用了表I中所示的参数值。

3) 外部驾驶人模型

VISSIM®的外部驾驶人模型（EDM）应用程序接口提供了对所有车辆或其子集的各种驾驶行为方面的访问。本研究中利用该接口来模拟哨兵系统在高速公路事故期间的运行。

每种情况的第一次仿真均使用VISSIM®的内部模型运行所有车辆，作为后续比较的基准情况。在后续的仿真中，EDM（事件驱动模型）仅影响事件期间最右侧车道上SE车辆的行为（即在3600秒至5400秒或7200秒之间，具体取决于事故持续时间）。在现实世界中，当哨兵系统通过本节开头描述的任何方法获知前方道路发生事件时，便会启动

比VISSIM®默认使用的欧洲车辆略大。

表I 驾驶行为参数
前方道路发生事件时，通过本节开头所述的任一方法通知。
为了估算车辆在到达事故点之前成功变道的概率，“哨兵”系统需要了解该车辆的d、vi、μi、σi、gi和ti。
由于在我们的仿真中仅最右侧车道被封闭，因此EDM（事件驱动模型）只需知道d、v1,、v2、μ2、σ2、g2,和t2,，假设最右侧车道为车道1，其左侧车道为车道2。其中，d设为车辆到事故点的距离，v1设为车辆的速度。为了估算v2、μ2和σ2，EDM使用了车道2中前方最多820.21英尺（250米）或最多10辆车辆，以及自车后方最多492.13英尺（150米）或最多2辆车辆的数据。此范围与大多数智能车辆上安装的雷达探测范围相似。令m表示检测到的车辆数量，ui和rj、1≤i≤m且1≤j≤m−1分别表示这些车辆的速度及其车间距，EDM据此设定
v2= u¯= ∑
m i=1 ui
m , (2)
μ2= μ¯= ∑
m−1 j=1 log(rj) m −1 , (3) σ2= σ¯= std(log(rj)), (4)
其中std()是标准差函数。公式3和公式4基于车间距为来自同一对数正态分布的独立同分布随机变量这一假设。
临界间隙gi被设定为δvi+s0，其中δ和s0分别设为1.6秒和1米。尽管在现实中临界间隙具有随机性，并且取决于多种因素，包括周围车辆的相对速度和位置以及驾驶员激进程度，但我们的选择简化了模型，其保守特性（通常大于实际临界间隙）确保了换道的安全性[47]。最后，ti被设为3秒，因为VISSIM®的内部模型在该时间内完成一次车道变换[48]。在哨兵系统的实际应用中，gi和ti均可进行调整，以匹配不同驾驶员或自动驾驶汽车的行为特征。
此值分配过程的唯一例外情况是当v2处于区间v1±vl内，且vl为4米/秒时。
在这种情况下，我们设定v2= v1+ vl。这样做的理由可追溯到[34]，该研究显示当v1接近v2,时，相对行驶距离显著减少，导致概率大幅下降，这在现实中是不合理的。因此，进行了此项修改，以更准确地表示驾驶员在换道操作期间的驾驶员行为。

为了模拟哨兵系统，EDM（事件驱动模型）需要在每个时间步长计算上述概率。如果某车辆的概率降至某一阈值pl以下，EDM将指示该车辆进行变道。根据第二节‐A和直观理解可知，该概率随着与事件位置的距离减小以及相邻车道交通密度的增加而降低，因此pl可被视为衡量哨兵系统在拥堵边界上游多远距离处提醒车辆变道的指标。换句话说，如果pl非常高（接近1），则哨兵系统预计会在远离拥堵边界的位置就向车辆发出警告；而如果pl较低，则哨兵系统仅在车辆接近拥堵边界时才发出警告。

对于15种情况中的每一种，我们测试了不同的阈值pl，范围从0.999到0.6，以了解pl如何影响平均延误和交通流。与[35],[36],类似的问题是，在哨兵系统实施过程中遇到的一个问题是：当EDM（事件驱动模型）提示车辆进行换道操作时，该车辆（由VISSIM内部®模型驾驶）并未检查换道是否安全，经常在换道过程中穿过其他车辆。我们的解决方案是在EDM中构建一个机制，在开始换道操作[47]之前检查安全性（附近车辆的足够间距和相对速度）。该机制实现的详细信息见[35],[36]。

4) 数据处理与评估

平均延误，定义为自由流速度下的行程时间与实际行程时间之差，是我们选择的有效性度量指标（MoE）[45]。根据第二节‐B.1中定义的行程时间测量方法，VISSIM®计算了每辆车的延误。对于每种qi、r γi和pl的组合，我们计算了每次运行i 1 ≤i ≤ 12中所有车辆的平均mi、标准差si以及最大延误ai，并报告每个900秒间隔及整个分析期的m= 1 12∑12 i=1mi、s= 1 12∑12 i=1 si和a= 1 12∑12 i=1ai。

如前所述，在某些情况下，12次运行中有少数在完成前崩溃。因此，我们在[36],中采用我们的方法，在分析期的m,s和a计算中排除崩溃的运行，但在9000秒间隔的m,s和a计算中保留崩溃发生前最近的900秒间隔内的数据。例如，如果某次运行在6465秒时崩溃，则我们保留至6300秒的数据。对于崩溃次数超过2次的情况（即成功的仿真运行少于10次），在表II和表III中标注了成功的仿真运行次数。

III. 结果与讨论

交通的统计指标 fi 分析期内的延误结果在表II中显示为γi= 30分钟，在表III中显示为γi= 60分钟。在每张表中，结果根据qi的值（向下递增）和r的值（向右递增）划分为方块区域。在每个方块区域内，每一行提供了特定交通设置（qi、r和γi的组合）在特定pl值下的仿真结果，其中第一行为基准情况，后续各行从第二行开始向下依次减小pl值，起始值为0.999。对于每行方块区域，pl值在第二列中给出。此外，在每个方块区域内，各列表示平均延误、延误的标准差以及最大延误。除基准情况外，每行延误值旁边的括号中的数字表示相对于基准情况的百分比变化。例如，表II第六行第9、10和11列的数值表示在qi= 6400辆/小时、r= 70%、γi= 30分钟以及pl= 0.97条件下的仿真案例的平均延误、延误标准差和最大延误，括号内的数值表示相对于第三行基准情况的变化量。在此pl值下，平均延误相较于基准情况改善了17.7%，而延误的标准差改善了22.8%。最后，如第II‐B.4节所述，当崩溃的仿真次数超过2次时，用于计算结果平均值的有效仿真次数（即未出错完成的仿真次数）将在该案例平均延误值的右上角以superscript形式标出，并适用于代表该案例的全部三个数值。例如，对于qi= 7200辆/小时、r= 70%、γi= 30分钟且pl= 0.9的案例，共进行了12次仿真，其中有5次崩溃，其余7次用于计算结果。

初步观察结果表明，在所有交通设置（qi、r和γi的组合）下，哨兵系统在事件期间均成功改善了交通流，并在各项指标（平均延误、标准差和最大值）上减少了延误。然而，减少的程度取决于每种交通设置的参数以及所选择的pl值。因此，我们首先讨论结果中的一些总体趋势，然后重点分析一个仿真案例的结果并进行更详细的探讨：该案例为qi= 6400辆/小时、r= 40%和γi= 60分钟，在此情况下，所有pl值均使平均延误减少了约20%到30%。

表II和表III均显示，正如预期的那样，基准情况下的延误在事故持续时间γi较长时更高。它们还表明，对于持续时间较长的事件，延误的减少通常更大，特别是对于较大的r值。正如后文将进一步讨论的，这可归因于哨兵系统所带来的延误减少的连锁效应。结果还显示，平均延误随着qi的增加而增加，因为在较大的交通流下，行驶在封闭车道上的车辆在接近事故点之前更难在相邻车道找到可接受间隙，导致更多最后一刻变道，从而引发额外的交通中断和延误。此外，由于交通流量超过三车道道路的通行能力而引发拥堵，该系统的影响随着qi的增加而减弱。

在基准情况下，哨兵系统未启用，因此其渗透率r不会影响交通延误结果。当哨兵系统启用时，对于渗透率r为= 10%的情况，我们发现无论qi 和 γ i 如何，由于渗透率较低，其对结果的影响都较为有限，这符合我们的预期。我们还发现，延误的减少随着渗透率r的增加而增加，并且在渗透率r最大时达到最显著效果。r= 70%，平均延误的改善高达37%，表明所有车辆都能从Sentinel渗透率的提高中受益。至于pl，无法观察到明显的趋势。最后，我们发现标准差和延误的最大值在上述所有参数中的变化趋势与平均延误相似。

在接下来的分析中，我们需要定义一个新参数dl，称为车道偏离密度[36]。dl可被视作衡量车辆在到达阻塞点前最后一次离开封闭车道的时间‐空间速率的指标。更具体地说，如果在阻塞点前的某一时间段N内有若干车辆最后一次离开封闭车道，该时间段持续时间为T，对应的道路长度为D，则针对该T‐D时间‐空间区域的dl定义为
dl= N DT .
(5)
d l 的单位是（车道偏离）/（英尺·秒）。本文假设T= 100秒且D= 200英尺。

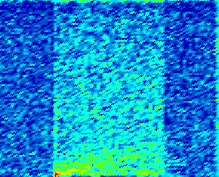
现在让我们深入分析qi= 6400 veh/hr、r= 40%和γi= 60 min的情况。对于该情况，图3显示了在分析期内每个900秒仿真时间间隔中，所有车辆的平均延误和放行率，以及不同pl值下的结果。图4和图5分别显示了普通车辆和SE车辆的类似图表。此外，图6显示了哨兵系统为一辆样本SE车辆计算的估计值P(S)（在到达事故点前离开被阻塞车道的概率），以及该车辆在道路上行驶时的速度，对应的情况为pl= 0.7。最后，图7显示了所有车辆的密度（单位：辆/英里）和速度（单位：英里/小时）的时空图，以及车道1中SE车辆的log(dl)时空图；图8显示了车道2中所有车辆的密度和速度的类似时空图。

在每张图中，第一列表示基准情况，其余三列分别表示pl= 0.999、0.9和0.7的情况。对于每个单个图表，横轴表示仿真时间，范围为1800至9000秒，即整个分析期；纵轴表示距离（单位：千英尺）。并覆盖整个道路段（21,054英尺）用于速度与密度图，而对于车道偏离图则仅覆盖至事故点（19,200英尺）。在车道偏离图中，我们绘制了log(dl)而非dl，以便更清晰地展示数值差异。此外，尽管速度与密度图使用了所有汽车的数据，但车道偏离图我们仅使用了SE车辆的数据。这是因为哨兵系统仅影响SE车辆的行为，而其他车辆的行为应与基准情况相比无统计学上的显著差异。

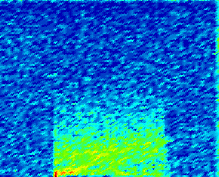
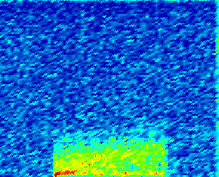
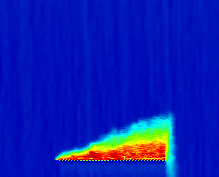
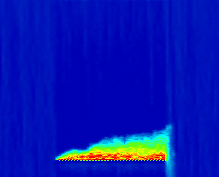
图6展示了哨兵系统在仿真过程中的运行情况。利用通过感知传感器获取的附近车辆数据，哨兵系统估算了自车在到达事故点前离开车道1的概率。我们可以看到，在前10,000英尺内，该概率接近1；但随着自车接近拥堵边界，车道2中的车辆开始减速并彼此靠近，该概率逐渐下降，直至低于0.7阈值。此时，哨兵系统建议自车在车道2中寻找可接受间隙以换出车道1。该车辆确实如此，因此，在即将到达事故引发的拥堵之前，如概率跃升至1以及速度降至零、反弹并再次重复此过程所显示的那样，呈现出走走停停的运动状态。

哨兵系统的工作原理有助于我们理解其对整体交通流的影响。如图5所示，在第五个900秒时间间隔（事件发生后的第一个时间间隔）内，哨兵帮助SE车辆提前离开车道1，从而相对于基准情况减少了其平均延误。图4表明，普通车辆的情况并非如此，其平均延误与基准情况几乎相同。第五个时间间隔的情况。图5进一步表明，对于SE车辆而言，平均延误减少的趋势在后续时间间隔中持续存在；与基准情况下平均延误呈线性增长相比，在哨兵系统运行的情况下，平均延误的增长速率低于线性增长。从图3和图4可以看出，这种行为减轻了拥堵，并间接改善了其他车辆相对于基准情况的平均延误。图3还显示，哨兵系统能够恢复部分因拥堵而损失的瓶颈通行能力。这表明，在哨兵系统运行的情况下，瓶颈通行能力约为6200辆/小时，接近三车道高速公路的名义容量，比基准情况高出近100辆/小时，其中SE车辆和普通车辆对通行能力的提升均有所贡献，如图4和图5所示。

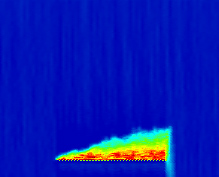
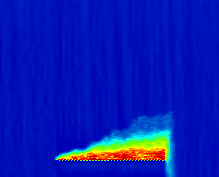
图7和图8从另一个角度说明了哨兵系统如何影响交通流。基准情况的车道偏离密度图显示，当事件发生时（3600秒与19200英尺交点），事故点附近出现大量的车道偏离激增现象，随着车道1的拥堵加剧，该现象沿道路逐渐扩散。相比之下，在其他三种情况下，事件发生点处的激增幅度要小得多，且车道偏离在事故点上游分布更为均匀。这不仅有助于降低车道1的交通密度，也降低了车道2的交通密度。这是因为SE车辆提前离开车道1并进入车道2，导致车道2上的一些汽车为保持三条车道的密度平衡而转移到车道3和车道4。而在基准情况下，大量汽车在事故点处涌入车道2，由于没有足够时间让其他车辆转移到车道3和车道4，导致车道2的密度迅速增加。

图7的车道偏离密度图还揭示了pl的选择如何影响车道偏离时机。如前所述，当pl较大时，哨兵会建议车辆比pl较小时更早地离开车道1。我们可以看到，对于pl= 0.999的情况，车道偏离沿道路均匀分布。这是因为交通中的任何微小扰动都会导致概率降至pl以下，从而使哨兵建议车辆离开车道1，即使车辆离拥堵区域还很远。相比之下，其他两种情况的车道偏离图显示，哨兵仅在车辆接近拥堵时才建议变道。对于这两种情况，图中显示，当pl= 0.9和0.7时，哨兵分别在事故点前约1.5英里和0.8英里处开始建议车辆离开车道1。尽管如此，表III表明，在这三个pl值中，该交通设置下平均延误减少最多的为pl= 0.999，其次是pl= 0.9。

总体而言，最优的pl选择取决于交通流、道路设置（车道数和封闭车道数）、事件持续时间以及哨兵系统的渗透率。然而，鉴于较大的pl值倾向于使变道位置远离事故点并更均匀地分布，我们推荐将pl值设在0.9到0.97范围内，以获得令人满意的性能。该值既不会过大（例如0.999）以随机建议车辆驶离车道，也不会过小以至于在接近拥堵时才建议车辆驶离车道。在更复杂的情况下，确定最优选择pl可能需要额外的交通仿真。动态分配pl可能是另一种解决方案，但该策略仍需进一步研究。

第四节 结论

本文介绍了哨兵（Sentinel），一种用于智能车辆的车载系统，在高速公路事故发生时引导其变道行为，旨在减少交通拥堵、通行能力下降和延误。哨兵通过利用车载感知数据、事故位置信息以及一个预测模型来实现这一目标，该模型使用交通相关和驾驶员相关参数，估计车辆在道路上通过一次或多次变道到达目标状态的概率。当检测到前方车道被事故封闭时，哨兵在每个时间步长计算车辆在到达事故点之前离开封闭车道的概率。当该概率随着车辆接近拥堵边界而降至某一阈值以下时，哨兵会建议车辆离开封闭车道。通过这种方式，哨兵减少了封闭车道内车辆在后期阶段进行干扰性变道的数量，并将这些操作分布到事故点上游。

使用VISSIM®进行了一项仿真实例研究，模拟四车道高速公路的一条车道因事件被封闭一段时间的情况，以了解“哨兵”系统对交通流的影响，以及不同参数——交通流、渗透率和事故持续时间——如何影响“哨兵”系统的性能。结果表明，“哨兵”系统对整体交通流具有积极影响，尤其是在渗透率较高时表现更为显著。该系统成功将交通延误平均减少10%或以上，并减轻了瓶颈处通行能力的下降。我们还观察到，在大多数情况下，“哨兵”系统的性能与概率阈值的选择关联不大，建议采用0.9到0.97范围内的概率阈值以获得满意的性能。

总体而言，哨兵系统在减少高速公路事故导致的延误方面的有效性、其简洁的设计以及易于实施的特点，显示出智能车辆广泛采用该系统的潜力，这有望每年节省因高速公路事故引发的拥堵所产生的数十亿美元成本。基于本研究的结果，未来的工作将侧重于利用全舱驾驶模拟器和实地实验来研究驾驶员合规性、哨兵系统在真实环境中的性能及其对驾驶行为的整体影响。