针对HIVE中RC4的实用攻击

针对HIVE隐藏卷加密系统中使用RC4的实际攻击

摘要

HIVE隐藏卷加密系统由布拉斯等人在ACM‐CCS 2014上提出。尽管HIVE具有安全性证明，但本文展示了一种针对其实现的攻击，该攻击破坏了作者所声称的系统主要安全属性，即对任意访问攻击者的可plausible隐藏性。我们的攻击之所以可行，是因为HIVE实现依赖RC4流密码将未使用块填充为伪随机数据。虽然通过使用更优的伪随机生成器可以轻松消除该攻击，但它仍是一个实例，说明为何在所有新应用中都应避免使用RC4，并提醒人们在实例化密码原语时必须格外谨慎。

1. 引言

在 ACM CCS 2014 上，布拉斯等人 [2] 提出了一种名为 HIVE 的新型“隐藏卷加密”系统。该系统将一个加密磁盘划分为多个卷。HIVE 的目的是隐藏其中某些卷的存在，并向观察者隐藏对这些卷的读写访问模式。

为了隐藏访问模式，读取和写入操作必须无法区分。为此，在读取操作期间通过用伪随机数据覆盖空块来模拟加密操作。HIVE实现使用RC4算法将数据块覆写为伪随机数据，并使用CBC模式下的AES执行加密。如果以下两者均安全，则该方法可被证明是安全的：由对称加密方案生成的密文和伪随机生成器的输出与随机字节无法区分。需要强调的是，在该方案中RC4并未用于加密任何数据，而仅用于以伪随机字节填充未使用的磁盘空间。根据[2]，选择RC4是出于性能原因。

我们指出，对于此任务而言，RC4 是一个糟糕的选择：我们证明，使用 RC4 使得我们能够破坏 HIVE 在 [2] 中声称的主要安全属性，即“对任意访问攻击者的合理隐藏”。事实上，我们将能够攻破针对 one-time 攻击者的更弱的合理隐藏概念。我们的攻击并不提取明文，但我们仅通过检查磁盘两次就能检测所谓的隐藏卷。此类攻击的不可行性被认为是 HIVE 相较于传统磁盘加密系统的主要优势，并被用来证明其存储开销[2]的合理性。

我们的攻击利用了RC4密钥流中的偏差。尽管众所周知RC4密钥流存在偏差，因此与随机字节流不可区分[5, 3, 4, 1, 6]，但这些已有结果是否可用于破坏HIVE所声称的安全属性并不明显。这是因为之前的区分器[3, 4]需要访问大量连续的密钥流字节，或相应数量的真实随机字节，而 HIVE以分块方式运行（典型的块大小为4096字节），向区分器提供的是短RC4块和AES‐CBC块的 mix。

我们的对手利用RC4密钥流中的曼廷偏差[4]，构建了一个针对短数据块的弱分块区分器；与之前识别RC4偏差的工作[3, 4]不同，我们明确提出了一种高效且接近最优的统计测试方法，可用于实现该区分器。然后，我们将此分块区分器在多个数据块上重复应用，以估计磁盘上有多少块被 RC4填充，以及有多少块被AES‐CBC密文填充；这种方法似乎是新颖的，在以往文献中尚未被利用。最后，该估计结果可用于判断HIVE系统在磁盘上执行了何种读取和/或写入访问序列。

我们的对手效率很高，且仅需对数据块进行适度数量的读/写查询。例如，在涉及对包含总计 2^24.7个数据块和104GB数据的磁盘进行 2^23.7次读写查询的攻击中，其成功率达到0.997。

我们的方法不涉及推导RC4的任何新性质。然而，它确实表明 RC4不仅是不适合作为通用的伪随机生成器（PRG）使用，而且在 RC4的弱点并不明显的情况下，也可能导致系统在实际中遭受攻击。

我们已在概念层面告知[2]的作者我们的攻击方法，并且尽管他们更新了HIVE系统1的常见问题解答，但他们最初并未借此机会修改其源代码以使用更安全的伪随机生成器，或修订描述该系统的研究论文。他们反而认为RC4只是一个可替换的构建模块，可以轻松地被替代。我们注意到，RC4是默认选项，而用户不太可能将其替换为自身实现的安全伪随机生成器，这使得他们面临风险。鉴于作者已将HIVE公开发布，并仍声称其“比所有现有方案提供更高的安全性”，2因此我们决定撰写本文，以提醒HIVE实现的潜在用户注意该系统的缺陷。

值得欣慰的是，在本文预印本发布后，HIVE实现中已用 AES‐CTR取代了RC4。

我们再次强调，我们仅针对使用RC4实例化伪随机生成器的HIVE具体实现进行攻击，并不声称若使用其他伪随机生成器实例化时HIVE方案是不安全的。事实上，我们认为 HIVE是一个非常有趣的提案，值得进一步的（密码）分析。

1.1 论文结构

在下一节中，我们将详细介绍HIVE及其对RC4的使用。在第3节中，我们构建了一个针对短数据块的RC4区分器。第 4节描述了如何利用该区分器攻击HIVE方案。

2. HIVE方案的描述

HIVE[2]是一种隐藏卷加密方案，其工作环境为划分为数据块的存储设备。用户选择一个值 l，然后最多可配置 l个逻辑卷 Vi，其中每个卷均使用从密码 Pi派生的密钥进行加密。在不知道相应密码的情况下，应无法检测到该卷的存在。其目标是：“即使对手已获取了用户磁盘的若干快照并知晓主卷的密码，用户仍能合理地否认隐藏卷的存在。”3 这使得有必要隐藏用户对磁盘的访问模式，这是通过构建一个仅写型不经意RAM（ORAM）方案来实现的。

原始论文提出了几种不同的安全概念和两种不同的方案；为了明确攻击目标，我们选择一种较弱的安全概念和一种方案，如下所述。为简便起见，我们假设所有ORAM的大小均为硬盘大小的 1/l倍。

2.1 ORAM

[2] 中提出的缓存优化的只写 ORAM 方案是一种将加密磁盘逻辑叠加在至少两倍于加密磁盘大小的物理磁盘之上的方案。该方案利用伪随机生成器（PRG）和一种对称加密方案，其特性是在没有密钥的情况下，密文与随机字符串不可区分。

ORAM 维护了逻辑块到物理块的映射关系。初始时，所有逻辑块都映射到 ⊥。在每次执行 ORAM.Write(逻辑块, 数据块) 操作时，ORAM 会随机（且与逻辑地址无关）选择 K 个物理块，并尝试解密每一个。其中一些可能已包含数据，而另一些可能是空的。待写入的新数据块以及已存储在所选 K 个块中的任何数据块都将被写入内存。具体来说，它们会被添加到一个 stash 中，该区域作为缓冲区用于存储尚未写入磁盘的数据块。然后，尽可能多地将暂存区中的数据块加密并写回到所选的 K 个块中。由于物理磁盘远大于逻辑磁盘，因此有很大概率所选的 K 个块中仍有一个或多个是空闲的，从而可以将暂存区中所有当前的数据块写入磁盘。从 K 所选块中剩余的空闲块则会被伪随机生成器（PRG）生成的随机数据覆盖。逻辑块到物理块的映射关系也会相应更新。

如果所选数据块中没有足够的空闲块，则一些数据块将保留在暂存区中，等到后续写操作时找到空闲块再进行写入。通常情况下，该方案的参数被设定为具有较大概率存在一个或多个空闲块，从而在高概率下使暂存区的大小始终保持较小。例如，对于 K= 3，暂存区中物品数量超过 50 的概率上限为 2−64。

安全论证在于，由于每次操作都会用伪随机字符串覆盖 K 个随机选择的数据块，因此该操作不会泄露任何关于逻辑地址、要写入的数据或磁盘状态（即哪些数据块是空闲的）的信息。

2.2 HIVE

HIVE的安全目标是隐藏未知密钥的加密磁盘卷的存在。这一目标通过在每次读取时执行一次真实ORAM.Read和一次虚拟 ORAM.Write，以及在每次写入时执行一次虚拟ORAM.Read和一次真实ORAM.Write来实现。

据[2]声称，HIVE 实现了针对任意访问攻击者的合理隐藏概念。我们将打破针对一次性攻击者的更弱的合理隐藏概念，该概念在紧随其下的定义1中给出。

Definition 1 (Plausible hiding). The experiment Expp l-ot-b AΣ ,(k for a bit b is run between an adversary A and a challenger emulating the schemeΣ and consists of the f ol-lowing phases.

1. In the setup phase, A sends l to the challenger who chooses l passwords P 1 … P l . The challenger initializes Σ 0 with l volumes and passwords and Σ 1 with l − 1 volumes and passwords P 1 … ,,, P l − 1 and sends P 1 … P l − 1 and a snapshot D 0 of Σb to A. ,,,.

2 In round i 1 to the challen g er; the challen g er executes o i A sends two accesses o i 0 and o i b onΣ b . ,，，，

3. Finally, the adversary requests a snapshot D f o f the disk which is the output o f the experiment. and outputs a bit b′ ，，

An access o is of the f orm o= then data d is written to block b on volume V. If op= r op b V d (,,,). If op= w,, block b from volume V is read into d. Since the adversary knows the passwords P1… Pl−1 ,,, if one of the operations in round i is a write to one of the volumes V1… Vl−1 ,,, then both operations must be identical. Intuitively this means, that any access to Vl can be passed off as an access to another volume.

We define the advantage of the adversary as
Advpl-ot A,Σ(k) = |Pr[1← Exppl-ot-0 A,Σ(k)] − Pr[1← Exppl-ot-1 A,Σ(k)]|.

If we used an asymptotic definition we would say that Σ is secure if for all PPT A pl-ot AΣ k ,Adv,() is a negligible func-tion. Since we want to attack a concrete instance , we use a concrete security definition. We fix a concrete security parameter k and let Advpl-ot Σ,k(τ, q)= max A{Advpl-ot A,Σ(k)}, where the maximum is taken over all adversaries running in at most τ steps and making at most q access queries(that is, there are at most q rounds in the game each round involving either writing to or reading from a single block). We then say that for a concrete parameter k -plausible hiding against one-time adversaries Σ is ε τ q if pl-ot Σ k τ q ≤ ε. ,(,,),Adv,(,)

2.3 HIVE 实例化

在 HIVE 中，对称加密方案通过 AES‐CBC 实现，使用 256 位由密码派生的密钥，并在每次调用时采用新的初始化向量 IV。每次操作写入的数据块数量 K（原始论文中为 k）在实现中被设置为 3。5 这个较小的 K 值需要使用未写入块的暂存区，以应对所选随机数据块全部已被使用的情况。根据 HIVE 源代码，卷初始未被随机数据覆盖。这对对手有利，因为这意味着需要考虑的额外数据更少，但该条件并非攻击成功的必要条件。

该实现遵循了良好的实践，即使用操作系统提供的真随机性进行一次种子初始化的伪随机生成器（PRG），以生成 HIVE中涉及的密码学操作所需的所有随机性。具体而言，伪随机生成器的输出用于： 1. 生成一个新的、随机的 16 字节 IV（用于每次调用 AES‐CBC）； 2用随机字节填充一个4096字节扇区； 3. 用随机字节填充一个32字节元数据块。一个元数据块由两个8字节值和一个16字节IV组成。 4.选择一个随机扇区进行写操作 w . 这需要一个用于扇区 ID 的随机 8 字节值。

伪随机生成器（PRG）在正确初始化后，使用RC4‐drop256进行实例化。根据[2]，这是出于性能原因。更具体地说，RC4使用从操作系统获取的256字节随机性作为密钥，取其前256字节为避免众所周知的强偏差（例如，参见[1]以全面了解这些偏差），RC4输出中的一些字节被丢弃，部分其他输出字节用于其他用途，然后使用B个连续的输出字节来填充一个包含 “随机”字节的数据块。HIVE实现采用 B= 4096（因此其数据块大小为4 KB），尽管[2]中也讨论了选择 B= 256的情况。需要注意的是，我们并不需要知道RC4密钥流中具体从哪个位置选取字节，而只需要知道这些字节是连续的即可。

3. RC4的分块区分器

在本节中，我们开发并评估了一种针对 HIVE 中使用的短 RC4 密钥流的区分器 D。该区分器将在下一节中用作构建针对 HIVE 攻击的一个组件。

3.1 RC4偏差

我们首先回顾一下来自[4]的关于RC4输出偏差的主要结果，这些结果将被我们使用。虽然还存在其他偏差，特别是[3]中的偏差，但在我们关注的场景中使用起来并不方便。这是因为这些偏差依赖于位置，而我们不希望对我们所针对字节在 RC4密钥流中的具体位置做出任何假设（因为从[2]中对 HIVE的描述及其相应的源代码来看，这一点并不明确）。

以下结果是对[4],中关于形式为 ABSAB的字节串在 RC4输出中出现概率的定理1的重新表述，其中 A和 B表示字节， S表示特定长度 G的任意字节串。

Result 1。 Let G ≥ 0 be a small integer. Under the assumption that the RC4 state is a random permutation at stepr, then
Pr(Zr= Zr+G+2 ∧ Zr+1= Zr+G+3) = 2 −16(1+ e(−4−8G)/256 256).

请注意，对于一个真正随机的字节串 Zr,…, Zr+G 3 ， Zr= Zr+G+2 和 Zr+1= Zr+G+3 等于 2 −16 的概率为 e(−4−8G)/256/256。因此，相对偏差等于 e(−4−8G)/256/256。

上述结果在[4]中通过实验得到了验证，适用于高达64的 G值，尽管样本量相当小，并且未聚焦于RC4输出的早期字节。我们已确认，在我们关注的情况下，该结果从位置256开始在合理近似下仍然成立。参见图1。

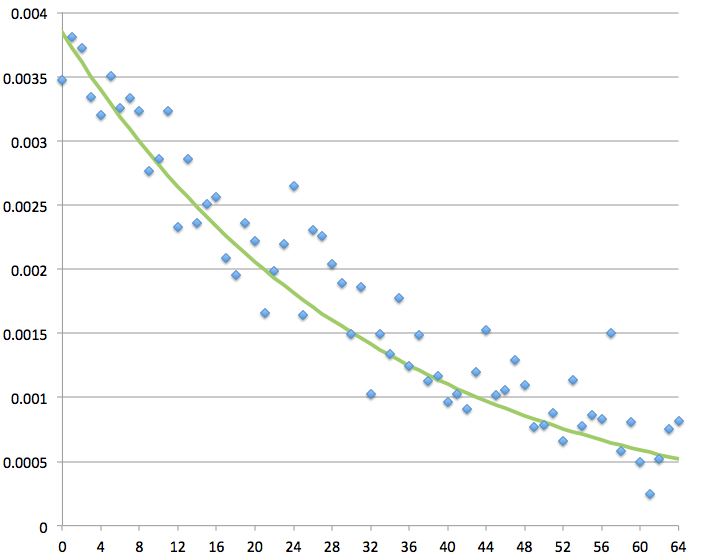
3.2 区分与统计假设检验

给定某个集合 S 上的两个概率分布 p 和 q，我们定义 p 与 q 之间的 discrimination，记作 L(p, q)，为 ∑s ∈ S p(s) log p(s)/q(s)。注意，该判别度是可加的：如果 p1 ,p2 , q1 , q2 是定义在 S 上的分布，且 p1 p 2 , q 1 q 2 表示 S × S 上的乘积分布，则有 L(p1 p 2 , q 1 q 2) = L(p1 , q 1) + L(p2 , q 2) 。此等式显然可推广至更大规模的分布乘积。

接下来考虑由基于Mantin“ABSAB”偏差的简单“偏差存在性”测试 T产生的分布 p 和 q 。该测试 T接收一个 B字节的字符串作为输入，查找一种特定类型的固定字节模式从固定位置开始，如果检测到该模式则输出1，否则输出0（这里我们假设偏差为正偏差，这与所有曼廷偏差的情况一致）。例如，该测试可能检查字符串中位置 r, r+ 1, r+ 2, r+ 3处的字节值四元组是否具有 “ABAB”的形式，如果输入字符串来自RC4输出而非真正随机的数据，则该事件发生的概率会略高于预期。

设 p为当输入字符串来自RC4输出时 T的输出概率分布， q为当输入字符串真正随机时 T的输出概率分布。则 p(0) = 1 −ρ(1+ γ)， p(1) = ρ(1+ γ)，且 q(0) = 1 −ρ， q= ρ (1)，其中 ρ= 2 − 16和 γ> 0为所考虑的相对偏差（因此对于某个小整数 G有 γ= e(− 4 − 8 G ) /256 /256）。

然后，如[4]中的引理3所示（使用不同的符号）， L(p, q) ≈ ργ 2。

不同位置存在不同类型的偏差，这促使我们考虑乘积分布 p1 · · · pt 和 q · · · q，其中这两个乘积中的每个分量对应于基于特定偏差的不同测试 Ti 。此处第二个分布始终是固定的分布 q（如上文所定义，因为当输入字符串真正随机时，所有偏差存在性测试的行为都相同），而第一个分布pi 描述了测试的{0, 1}值输出的分布来到 Oi。我们假设有 t 次测试，总共并对我们的 B 字节输入所能执行的所有简单偏差存在性测试相互独立。考虑到所进行的测试类型不同，尽管许多测试涉及重叠字节，这一假设似乎是合理的。在开发 RC4 的区分器时，[3, 4] 也做出了同样的假设。该假设使我们能够写出：

L(p1 · · · pt, q · · · q)=
∑
i=1
L(pi, q) ≈ ρ
∑
i=1
γ 2 i

其中 γi 是针对第 i 次测试执行的适当值。

设 D 表示基于输入的任意区分器，该输入是 t 个独立偏差存在性测试的输出 Oi 的级联，并用于预测在测试中使用的特定 B 字节字符串是由 RC4 生成的还是真正随机的。我们假设当输入来自 RC4 时， D 以概率 1 − β 输出1（表示 RC4）；而当输入真正随机时， D 以概率 1 − α 输出0 （表示真正随机）。换句话说， α 是 D 的误报率， β 是 D 的漏报率。那么，根据 [3], 可得：

L(p1 · · · pt , q · · · q) ≥ β log 2
β 1 − α +(1 − β) log 2
1 − β α .

此外，任何最优统计检验（例如内曼‐皮尔逊似然比检验）都能达到等号成立。接下来，我们针对在连续密钥流字节的 B字节块中出现的所有可能的曼廷偏差对应的测试集，评估 Lp1 · · · pt, q · · · q ≈ ρ∑t i=1 γ 2 i。根据上述公式，这将使我们能够为最优区分器 D建立(α, β)的界限。然后，我们基于这些曼廷偏差提供一种高效且近似最优的统计检验，并以最大化量 1−α−β的方式计算该检验的参数，该量即为区分器 D的通常优势。

3.3 曼廷偏差的计算

在一个 B 字节的块 b 中，我们可以对每个 G ≥ 0 的值执行 B−(G+3) 偏差存在性测试，并使用 γ= e(−4−8G)/256/256。实际上，由于偏差的大小随着 G 的增加而减小，因此我们处理满足 0 ≤ G ≤ Gmax 的 G 值，其中 Gmax 为某一取值。在我们的实验中，我们取 Gmax= 64。结合所有这些偏差存在性检验，我们得到 t= ∑Gmax G=0 B − G+3 ≈ Gmax · B () 个检验方法，使得
L(p1 · · · pt, q · · · q)= ρ∑ G≥0 (B −(G+3)) · e(−4−8G)/128/216).

直接计算得到 L ≈ 8.7276 ≈ ×10−7 p1 · · ·pt q · · · q B= 256 Gmax= 64 B= 4096 (,)，当 且 。对于 和Gmax= 64，我们得到 L(p1 · · ·pt, q · · · q) ≈ 1.4914 × 10−5。

3.4 一种高效的统计检验

我们从似然比检验开始，并由此开发出一种高效的近似最优检验方法。

在似然比检验中，检验统计量被计算为比率 Λ(O) := L (θ0|O)/L(θ1|O)，其中 θ0 表示由假设 H0 产生的分布， θ1 表示由备择假设 H1 产生的分布， O 表示观测到的数据，而 L(θi|O) := Pr(O|θi) 表示似然。在该检验中，如果似然比 Λ (O) 小于或等于某个值 η，则拒绝假设 H0（并且我们的区分器输出1，表示其输入被认为是 RC4）；否则，接受 H0 （并且我们的区分器输出0，表示其输入被认为是真正随机的）。

原则上， η 可以从 α（即该检验的误报率）计算得到。具体而言， η 被确定为使得 Pr(Λ(O) ≤ η|H0)= α 成立的值。

在我们的情况下， O是由具有参数 γi的各个测试 Ti的结果Oi组成的向量。假设H0是输入的 B字节序列是随机的，而 H1是该序列为RC4输出的假设。考虑到对所有 i均有 γ i > 0，我们可以写出
L(θ0|O)= ∏ i:O i =1 ρ ∏ i:O i =0 1 − ρ
and
L(θ1 |O)= ∏ i:O i =1 ρ(1+ γ i) ∏ i:O i =0 1 − ρ(1+ γ i) .

然后，取对数，利用 ρ和所有 γ i 都很小的事实，使用标准对数近似方法处理上述表达式，并进行化简，最终得到：
logΛ(O) ≈ − ∑ i:O i =1 γ i + ∑ i:O i =0 ργ i .

让我们用 L 表示上述量。因此，一个合适的、近似最优的检验方法是拒绝假设 H0 （输入字符串是真正的随机字符串），如果 L ≤ log η则输出 “1”，否则输出“0”。注意检验统计量 L的计算是高效的： 它需要大约 Gmax · B次浮点运算和字节比较。

接下来需要为给定的目标 α 计算合适的 η 值。这要求我们知道当 O 来自分布 θ0 时，检验统计量 L 的分布情况。在此情况下，结果 Oi 服从参数为 ρ 的伯努利分布，即 Pr(Oi= 1) = ρ。此外，我们可以将测试分为 Gmax+ 1 组，每组对应于具有相同 γi 值的一组测试。由于每组中的测试数量较大， L 中相应项的和可以用正态分布来近似，其均值和方差可以显式计算。原则上，这使得可以计算 L 的分布。我们省略具体细节。

3.5 参数的最优选择

出于下一节将变得清晰的原因，我们希望在作用于 B字 节输入的区分器 D的选择上，最大化量 δ= 1 − α − β的值。让我们将此值记为 δB。（作为临时动机，注意 δ是区分器的优势的通常密码学定义。）由于我们关注最优区分器，因此我对参数(α, β)的选择受到以下约束： LB= β log2 β 1−α +(1 − β) log2 1−β α ，其中量 LB已在第3.3节中针对不同的 B值 进行了计算。使用Wolfram Alpha6进行直接最大化得到 δB= 0.00055（在(α, β) =(0.499459, 0.499991)处）和 δB= 0.002273（在(α, β) =(0.498343, 0.499384)处）。

3.6 实现

我们实现了上述统计检验，以确保其实际性能与理论分析一致。如上所述，参数 η 可通过计算检验统计量 L 在 O 来自分布 θ0 时的分布来设定。另一种方法是生成大量检验统计量的样本，以估计 L 的分布，并通过计算样本值的 α‐百分位数来设定 η。

在我们的实验中，我们简单地设置 η= 0，在随机输入和RC4输入上运行测试，并计算对应的 α, β, δ值。这使我们得到的 δ值并非最优，但足以验证该测试有效，并为我们提供一个性能接近理论可达到水平的区分器。对于B= 4096 ，基于 2 25个样本（随机输入和RC4输入各2 24个），设置 η= 0， 我们获得了α= 0.453706、 β= 0.544646和 δ= 0.001648。此处 δ的值与理论最大值0.002273相比表现良好。我们相信通过调整 η可以获得更接近的结果。在接下来对HIVE攻击的评估中，我们将给出理想情况下 δ值以及实验获得值的攻击成本。

4. 基于分块RC4区分器的HIVE攻击

我们描述了一类由块长度 B 和另外两个参数 S 参数化的对手 {AB, S ,T} T，其定义如下。我们的对手可以访问第3节中作用于 B字 节的区分器 D。回顾一下， D输出单个比特 b；如果 D的 输入是均匀随机字节，则 DB以概率 α输出1；如果 D的输入 由 B个连续的RC4输出字节组成，则 D以概率 1 − β输出1。

对于固定的块长度 B, AB,S,T，这是一个针对两个卷的合理隐藏的一次性对手，如定义1所述。在此简单情况下，存在两个由密码 P1, P2 保护的加密卷 V1,V2，而用户希望对已知 P1 的对手否认 V2 的存在。我们为简便起见考虑两个卷，且因为实现中使用了两个卷；该攻击可直接推广到任意数量的卷。我们假设每个卷由 S 个大小为 B 字节的数据块组成，因此磁盘总共有 4SB 字节（因其需要为所有卷总大小的两倍）。

我们将定义1中的访问操作符号进行了重载，以允许在单个查询中读取和写入多个数据块。下文中， 0SB表示一个由 SB字 节组成的全零字符串，相当于 S个每块 B字节的数据块。

我们的对手 AB,S,T 随后分五个步骤进行：

1. AB,S,T向挑战者发送 l= 2 并接收密码 P1 和磁盘的快照 D0。
2. AB,S,T发送 o1,0= o1,1=(w, 0, V1, 0 SB)。
3. AB,S,T sends o2,0=(w, 1, V2, 0SB), o2,1=(r, 0, V1, d, SB).
   4 AB,S,T请求一个快照 Df，其中包含 4S个数据块 . AB,S,T忽略与D0中相同的数据块，对 Df中剩余的 E 个已使用的数据块依次运行 D ，并将D的输出位连接起来形成字符串 R ∈{0, 1} E。
4. 最后，AB,S,T在 W的汉明重量 R至多为 T时输出1；否则输出0。

以下定理是显然的（注意读取或写入 B字节在之前给出的安全模型中计为1次查询，因此AB,S,T总共进行了 2S次查询）：

Theorem 1. Let τ B, S T and S T its advantage. Then HIVE is not B S B S T ,, T denote the running time o f AB,, Adv ,, (Adv,, , τ B S T ,, , 2S) -plausible hiding against one-time adversaries.

现在让我们确定定理能够给出有意义攻击的 S、 B和 T 的取值。我们考虑在安全实验中当 b= 0和 b= 1时，AB,S, T在其攻击过程中所能获取的信息。当 b= 0时，磁盘使用 V1 和 V 2进行初始化，并执行 o 1,0和 o 2,0。当 b= 1时，磁盘仅使用 V 1进行初始化，并执行 o 1,1和 o 2,1。

对手在任何操作执行之前获得了磁盘的初始快照，因此识别未使用块是很容易的； E表示在D0 和 D f 之间不同的数据块数量。所有被写入的数据块必然不同，因此我们有 2S ≤ E ≤ 4S。我们将 EB称为有效磁盘大小，因为其他数据块与攻击无关。注意 E的期望值约为 3.1075S。（磁盘上有 4S个数据块，在我们攻击中的 2S次读和写操作中， HIVE将随机选择 K · 2S= 6S个数据块进行写入。这意味着我们预期在总共 4S个可用数据块中，有 4S ·(1 − 1 4 S) 6 S 数据块 not被写入。7利用 (1 − 1/n)m ≈ e−m/n，我们得到 E[E] ≈(1 − e−1.5)4S ≈ 3.1075S。

设 Wb表示由AdvB,S,T在情况 b下构造的向量 R的汉明重量。我们有：

当 b= 0时，有 2S个数据块被写入磁盘，因此其中包含 2S个AES输出数据块和 E − 2S个RC4输出数据块。由于AES输出无法与随机数据区分（否则我们将能够对AES发起攻击）， W0的期望值为 α · 2S+(1 − β) ·(E − 2S)。

当 b= 1时，仅有 S个数据块被写入磁盘，因此其中包含 S个数据块的AES输出和 E − S个数据块的RC4输出。W1的期望值为α · S+(1 − β) ·(E − S)。

因此，两种情况下 R的汉明重量的期望值之差为(1 −α −β)S= δS，这对应于情况0中写入磁盘的额外 S数据块。

注意， D 对每个 B 字节块的输出是一个独立的伯努利随机变量，其服从两种可能分布中的一种，具体取决于该块包含的是 RC4 输出还是 AES 输出（我们假设后者与真正随机字节无法区分）。具体而言，当一个块包含 RC4 输出时， D 的输出以概率 1 − β 等于 1；而当它包含 AES 输出时， D 的输出以概率 α 等于 1。因此，当 b= 0 时， W 的分布是一个参数为 p1=…= p2S= α、 p2S+1=…= pE= 1 − β 的泊松二项分布（由于各次试验相互独立，顺序无关紧要）。类似地，当 b= 1 时， W 的分布是一个参数为 p1=…= pS= α、 pS+1=…= pE= 1 − β 的 泊松二项分布。

根据泊松二项分布的标准结果， W0 的方差等于 2Sα(1−α)+(E−2S)β (1−β)，而 W1 1− β Sα 1−α+ E−S β α 1 − α β 1 − β ≤ 1/4 E ≤ 4S 的 方差等于 ( ) ( ) ( )。由于 ( ) ( ) 且 ，因此这两个方差均被 S 所限制。我们定义 σ 2:= S。

现在，考虑到 W0 和 W1 是大量独立伯努利随机变量的和，我们可以将其近似视为正态分布（这里我们假设 E 足够大，实际上也必须如此才能使我们的对手获得合理的成功率）。

我们已经确定它们的方差以 S 为界，而它们的均值相差 δS。我们设 T T= E − 1.5S − 1.5Sα − E − 1.5S β 为均值 的中间点；即( )。这最终使我们能够应用正态分布的标准尾部界限，以估计AB, S ,T的优势。

假设我们坚持要求 W 0 , W 1 的均值相距为某个参数 n；那么根据我们对 T的选择以及

n	AdvB,S,T	log2 S(理想情况)	log2 S（实验）
1	0.683	19.6	20.5
2	0.954	21.6	22.5
3	0.997	22.7	23.7

表1：为达到给定优势AdvB,S,T，所需的数据块 B= 4096数量

在我们的正态性假设下（并且由于 σ2是 W0, W1方差的上界）， 我们得到对手的优势至少为
1 − erf( n √2)

其中 erf(·) 是正态分布的标准误差函数：
erf(x)= 1 √π ∫ x −x e−t2 dt.

因此，在条件 δS= 2nσ= 2nS1/2下，我们对手AB,S,T 的优势AdvB,S,T至少为声称值，即 1 −erf(n/√2)。求解 S， 我们得出所需条件
S= 4n2 δ2
以实现所声称的优势。

4.1 具体数值

为了发起一次具体攻击，我们设定 B= 4096，如[2]所示。然后，根据第3节的结果，我们可以将 δ= 0.002273作为最优设置。在上述分析中设定 n= 1并求解 S，得到优势为0.683时的 S= 219.6。继续计算其他 n的取值，我们得到了表1中的第二列。因此可以看出，通过设置S= 222.7，即可实现一个优势接近1的对手，也就是说，该攻击涉及在包含总共 4S= 2 24.7个数据块和4BS= 2 36.7字节数据（即大约104GB数据）的磁盘上进行 2S= 2 23.7次读写查询。

表1中的第三列包含了基于设置 δ= 0.001648对 S的估计值，该值是在第3.6节中开发的统计检验中设置 η= 0时实验观测到的。该列中较高的数值反映了分块区分器在此 η设置下的次优性能。

实施该攻击的主要计算成本在于运行分块区分器 E 次； 由于 E ≤ 4S，攻击的总成本约为 Gmax · B · S 次浮点运算。在我们的实现中，对于 Gmax = 64、 B= 4096，在配备 1.3 GHz Intel Core i5 处理器和 8GB 内存的 MacBook Air 上执行一次 single 的分块区分器的运行时间为 0.000719 秒；因此，当 E= 4S 和 S= 2 23.7 时，整个攻击的运行时间约为 11 小时。通过优化 η 的选择（从而允许降低 S 的取值），该运行时间可以进一步改善。

类似的计算可以使用 B= 256进行，其中我们可以取 δ= 0.00055。我们得到表2。可以看出， S需要更大，这反映了当块大小较小时，我们的分块区分器性能明显更弱。另一方面，总磁盘容量为

n	AdvB,S,T	log2 S(理想情况)
1	0.683	23.6
2	0.954	25.6
3	0.997	26.8

表2：为达到给定优势 AdvB,S,T 所需的数据块 B= 256 数量

只是适度增加，并且由于块大小减小，区分器的运行时间进一步减少。

5. 结论

我们已证明，当前使用RC4的HIVE实例是不安全的。具体而言，存在一种高效攻击，该攻击涉及对 B= 4096字节 数据块进行 223.7次读写查询，且我们可在此针对一次性对手的合理隐藏安全模型中构建出具有0.997优势的对手。这违反了HIVE所声称的主要安全属性。

我们的工作表明，如果使用不安全的原语实例化一个可证明安全的方案，则所有安全保证都可能丧失。

通过使用更强的伪随机生成器（PRG）替换RC4，可以修复HIVE。例如，可以改用计数器模式下的AES（CTR）； 这不仅更安全，而且在具备AES硬件支持的平台上，其性能将优于当前基于RC4的系统。eSTREAM项目还提供了更多针对硬件或软件性能优化的可选方案。8

我们曾向HIVE的作者通报了我们对其方案依赖RC4的初步担忧，并给予他们机会修改代码和论文，但他们并未利用这一机会。鉴于HIVE已向公众发布，并被宣传为“not rely[ing] on heuristics or obfuscation techniques, but rather strong cryptographic primitives which can be mathematically proven”，并声称能够“provide very strong security in practice” 9 ,，我们决定完善并发表我们的攻击方法，以明确展示使用RC4实例化该系统的缺陷。

在本文预印版发布不久后，HIVE实现中的默认PRG由 RC4更换为AES‐CTR。据HIVE开发人员称，I/O性能未受影响。10