Mamba模型(Mmaba1, 没有mamba2)

原创 已于 2024-07-23 15:31:38 修改 · 1.6k 阅读 · 17 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#深度学习 #cnn #神经网络

于 2024-06-21 14:41:23 首次发布

问题

Transformer模型基于矩阵乘法，注意力机制中Q、K、V（N×d）会进行大量运算。

如：使用Q、K运算得到score的过程中，将Q每一行与K每一列进行运算，需要N^2次点积，每次点积包含d次乘法。即最终的复杂度为O(N^{2}d)。考虑到序列长度（L）、batch大小（B）、多层Transformer块的堆叠（M），计算量为M\cdot (24bLd^{2}+4bL^{2}d),参考。

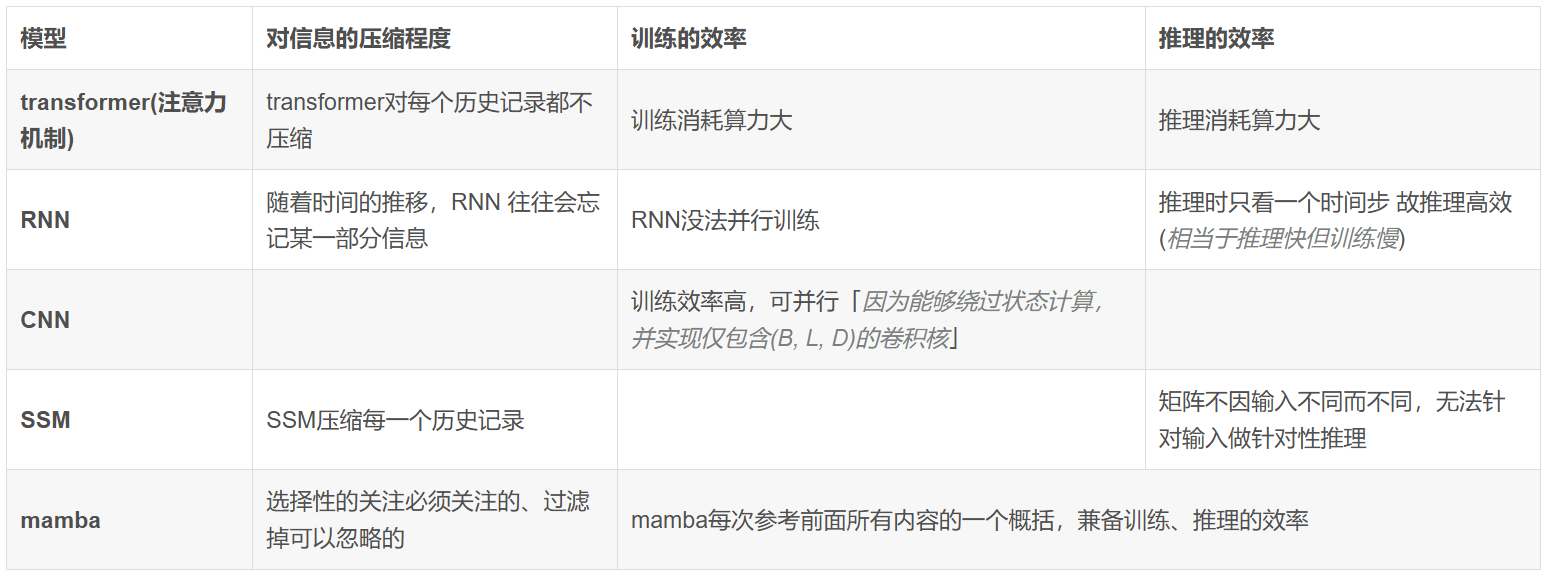
RNN存在梯度消失的问题，且训练时间长。

状态空间模型

Mamba中的状态空间模型（SSM）的灵感来源于传统的状态空间模型，公式描述如下：

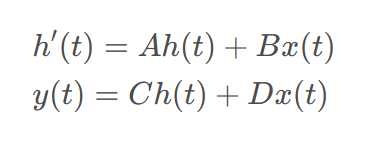
其中，h ( t ) h(t)h(t)是当前的状态量，A AA是状态转移矩阵；x ( t ) x(t)x(t)为输入的控制量，B BB表示控制量对状态量的影响。y ( t ) y(t)y(t)表示系统的输出，C CC表示当前状态量对输出影响，D DD表示当前控制量对输出影响。

这个模型是时不变(time-invariant)系统，时不变系统是输出不会直接随着时间变化的系统。任意时间延迟的输入将得到相同时间延迟的输出（ABCD其实可以带上时间参数，那就是时变系统，延时输入会导致不同的输出）。

离散化

 为了方便运算，将上述状态空间模型离散化，使用零阶保持法。 离散近似的结果为：

其中I为单位矩阵

 卷积化

 Mamba中的状态空间模型计算效率最大的提升就在于其序列运算可以卷积化。从0时刻开始向后推导状态空间模型几个时刻后的输出，即可得到如下的形式：

设计适当的卷积核即可将序列运算转化为卷积运算，形式如下所示：

 见解：设序列长度为x。使用高性能的卷积模式进行运算时会使用输入的所有信息预先计算K(0...x-1)，最后直接与对应位置输入相乘即可。即这时Mamba是非因果的，每个点使用了未来的信息。

 选择性机制

传统状态空间模型的时序结构导致了其输出状态完全依赖有序的输入数据。对于增减过、顺序打乱过的输入，在一些不相关数据混杂在序列中出现时，状态空间模型就无法对其进行有效处理。

Mamba针对这一情况进行了改进，在对B BB，C CC矩阵进行计算时，加入了选择性机制，即在计算是引入一个额外的线性层，对输入的输入的控制量和状态量进行选择，加强模型对不同输入形式的适应能力

 选择性机制对状态空间模型的改进

并行累加计算流程 

mamba结构

与Transformer结构类似，Mamba结构也是由若干Mamba块堆叠而成。一个基本的Mamba块结构如图所示：Mamba块由H3块以及门控MLP组合而成。H3为Hungry Hungry Hippos，是一种状态空间模型的执行方式。Mamba块简化了H3的结构，并与门控MLP结合，添加了残差项防止梯度消失。

使用mamba搭建模型一般会包含3个类似残差连接的部件：SSM内部的D，Mamba中除去SSM的另一条分支最后与SSM结果相乘，Mamba块外，即模型搭建时的残差连接

使用高效硬件乘法时先计算非离散化参数，送至GPU的SRAM(据我所知应该是share memory)中进行离散化及SSM运算，再回传到普通内存(HBM)。

此外，SSM正向传播并不会保存形状为（B, L, D, N）的中间状态以供反向传播训练，而是在反向传播时重新计算，与将其保存到HBM并读取相比，重新计算的耗时更短。

参考：

一文通透想颠覆Transformer的Mamba：从SSM、HiPPO、S4到Mamba_mamba模型-优快云博客

Mamba模型底层技术详解，与Transformer到底有何不同？-优快云博客

Mamba：2 状态空间模型 - 大模型知识库|大模型训练|开箱即用的企业大模型应用平台|智能体开发|53AI

 原文代码：mamba/README.md 在 main ·状态空格/曼巴 (github.com)

论文：[2312.00752] Mamba：使用选择性状态空间的线性时间序列建模 (arxiv.org)

参考代码：mamba-minimal/README.md at master · johnma2006/mamba-minimal (github.com) 

phoenixlxl
关注
深入理解 Mamba：从SSM到SSSM的公式推导
yuride的博客
06-23 1511
Mamba：一种高效处理长序列的新型状态空间模型 Mamba模型突破传统序列建模瓶颈，通过状态空间模型(SSM)实现线性时间复杂度的长序列处理。其核心创新在于将连续系统离散化，并通过动态参数调整适应时变数据特性。相比RNN和Transformer，Mamba兼具O(n)计算效率和长距离依赖建模能力。模型采用零阶保持法实现离散化转换，并引入时变参数Bt和Ct，使系统能动态适应语音、金融等时序数据的瞬时变化，同时保持基础矩阵A的稳定性。这种设计使Mamba在保持运算可追溯性的同时，实现了对时变序列的高效建模。
Mamba和状态空间模型(SSM)的视觉指南：替代 Transformers 的语言建模方法
安静的软件工程师
03-31 4486
Mamba和状态空间模型(SSM)的视觉指南：替代 Transformers 的语言建模方法
Mamba 模型
skyxya的博客
06-26 2701
虽然这个概念与模型架构的特定选择无关，但现代 FM 主要基于一种类型的序列模型：Transformer 及其核心注意力层自注意力的功效归因于它能够在上下文窗口中密集地路由信息，使其能够对复杂的数据进行建模。此外，论文提出了一类新的选择性状态空间模型，它在几个轴上改进了先前的工作，以实现 Transformer 的建模能力，同时在序列长度上线性缩放。选择性 SSM，和扩展 Mamba 架构，是具有关键属性的完全循环模型，这使得它们适合作为在序列上运行的一般基础模型的主干。
Mamba：2 状态空间模型
鲁班模锤
05-06 1784
Mamba自从出道就一直被拿来和Transformer对比，文章巨多，带着标题的爆炸性字样“颠覆Transfomer”，“全面包围”等等。文章深浅不一，小编认为其背后的设计思路以及演化过程更加重要。为此本专题将从山上有座庙开始，沿着RNN、SSM、S4、HIPPO一路走来。期间抛弃冗杂的文辞，以更接地气的模式协助读者打开新的逻辑思维。
【论文阅读笔记】Mamba模型代码理解
热门推荐
寸先生的AI道路
04-07 2万+
Mamba模型代码实现及理解
深度学习基准模型Mamba
06-30 2401
综上所述，MAMBA模型以其创新的选择性结构和高效的信息处理机制，为序列建模任务提供了一个有竞争力的解决方案，旨在克服现有模型在处理长序列数据时面临的挑战，同时推动深度学习技术在序列分析领域的进步。(英文直译：眼镜蛇)具有选择性状态空间的线性时间序列建模，是一种先进的状态空间模型 (SSM)，专为高效处理复杂的数据密集型序列而设计。
mamba 2 windows （cuda12.4）安装包，包括causal-conv1d，mamba-ssm
01-09
参考博客https://blog.youkuaiyun.com/yyywxk/article/details/145018635，有问题请加博客文末vx 注意，python，torch以及cuda版本必须要和博客里一致。 支持算力为6.0-9.0 等目前常见GPU。
mamba 2 windows安装包，包括causal-conv1d，mamba-ssm， selective-scan-cuda
11-20
参考博客https://blog.youkuaiyun.com/yyywxk/article/details/143924743，有问题请加主页vx 注意，python，torch以及cuda版本必须要和博客里一致。 支持算力为7.0-9.0 等目前常见GPU。
深度学习领域中基于Transformer与Mamba2的混合预测模型及其高效特征权重学习的应用
05-30
内容概要：本文介绍了结合Transformer和Mamba2的预测组合模型。Mamba2作为新一代的状态空间模型（SSM），以RNN方式通过隐藏状态映射序列，实现了计算和内存与序列长度的线性扩展。该模型被插入到Transformer前端，...
基于Transformer与Mamba2的时间序列预测模型：特征权重学习的端到端解决方案
04-17
内容概要：本文介绍了一种将Mamba2状态空间模型与Transformer相结合的时间序列预测模型。Mamba2用于特征权重学习，减少计算量并提高训练速度，而Transformer专注于捕捉全局依赖关系。作者详细展示了模型的设计思路、...
ML-Mamba : 利用Mamba-2的高效多模态大型语言模型
u014546828的博客
08-25 1434
多模态大型语言模型（MLLMs）因其多功能性而备受关注。然而，传统的Transformer架构由于其二次计算复杂度而产生了显著的开销。为了解决这个问题，本文引入了ML-Mamba，这是一个多模态语言模型，它利用最新且高效的Mamba-2模型进行推理。Mamba-2以其线性可扩展性和对长序列的快速处理能力而闻名。本文将基于Transformer的主干替换为预训练的Mamba-2模型，并探索将二维视觉选择性扫描机制集成到多模态学习中的方法，同时尝试各种视觉编码器和Mamba-2模型变体。
深度学习基础模型之Mamba
始于足下
03-30 5208
这项基础性模型研究旨在解决transformer模型的长序列数据计算效率低的问题，其解决方法的动机：利用选择性机制实现有效特征的提取。个人理解为通过有效特征信息的选择实现知识提取（信息压缩），这让我联想到，最初的VGG网络结构设计其实类似于模拟知识特征的压缩与抽取，但后来发现这种方式会损失边缘信息，因此提出了U-net架构，再进一步卷积的方式无法有效估计全局上下文信息的联系，进而提出注意力机制来解决这一问题。
【论文阅读】Mamba：具有选择状态空间的线性时间序列建模
1
01-31 5266
Mamba模型是一个创新的线性时间序列建模方法，巧妙地结合了递归神经网络（RNN）和卷积神经网络（CNN）的特点，解决了处理长序列时的计算效率问题。它通过状态空间模型（SSM）的框架，实现了RNN的逐步处理能力和CNN的全局信息处理能力的融合。在训练阶段，Mamba使用卷积模式来一次性处理整个输入序列，而在推理阶段则采用递归模式，逐步处理输入，这样的设计使得Mamba既能充分利用CNN的高效并行处理能力，又能保持RNN在序列数据处理上的灵活性。 ​ Mamba模型的核心创新在于引入了选择性机制，这一机制通
【转载】解读Mamba序列模型
SmartLab307的博客
05-07 4061
他在SSM的基础上，通过此篇论文《》首次提出了结构化状态空间S4(这里有关于S4的更多论文)，但这篇论文的可读性比较差；当然，作者在YouTube上有一个关于这篇S4论文的精彩解读，比S4论文的可读性提高很多，且本文中也应用了其中的部分PPT截图，但还可以更加通俗易懂；此外，Maarten Grootendorst写了一篇《A Visual Guide to Mamba and State Space Models》，可读性较强。
【论文阅读】Mamba:选择状态空间模型的线性时间序列建模（二）
weixin_45668967的博客
03-05 2046
我们的简化块设计结合了H3块，H3是大多数SSM结构的基础，有现代神经网络中无处不在的MLP块。因此，虽然选择机制可以被视为架构门控、超网络或数据依赖性等思想的特例，但大量其他结构也可以——基本上是任何具有乘法运算的结构，也包括标准注意力机制，但我们认为这样没有信息量。如在部分3.1讨论的一样，选择性最重要的属性是过滤掉我们不相关的信息以使一个序列模型的内容可以被压缩到哟个有效的状态。选择机制是一个广泛的概念，可以以不同的方式应用，例如在更传统的RNN和CNN，在不同的参数（例如算法2中的。
Mamba 来了：选择性状态空间模型（第三部分）
2401_85233349的博客
09-04 3420
第 3 部分 - 面向图像、视频和时间序列的 Mamba 状态空间模型 添加图片注释，不超过 140 字（可选） 米amba，这个被认为可以取代强大的 Transformer 的模型，从最初在深度学习中使用状态空间模型 (SSM) 的想法已经走了很长一段路。 Mamba 为状态空间模型添加了选择性，从而实现了与 Transformer 类似的性能，同时保持了 SSM 的亚二次工作复杂度。其高效的选择性扫描比标准实现快 40 倍，并且与 Transformer 相比，吞吐量可提高 5 倍。 与
【模型架构】学习最火热的Mamba、Vision Mamba、MambaOut模型
cjy_colorful0806的博客
06-01 8233
状态空间模型（State Space Model, SSM）是一种用于描述动态系统的数学模型，特别适用于时间序列分析和控制系统设计。它将系统的状态表示为一个状态向量，并通过状态方程和观测方程描述系统的动态行为和观测过程。因此，SSM是可以用于描述这些状态表示并根据某些输入预测其下一个状态可能是什么的模型，这就符合了作为深度学习模型基础架构的条件。SSM的计算示意图具体来说，可以用下面的公式描述上述过程：状态变量：描述系统当前状态的变量。状态变量通常是一个向量，包含系统当前时刻的所有信息。
最新模型VMamba：颠覆视觉Transformer，下一代主流Backbone？
soaring_casia的专栏
02-06 5130
卷积神经网络（CNN）与视觉Transformer（ViT）是目前最流行的两种视觉表征基础模型。CNN在线性复杂度下，具有惊人的可扩展性。ViTs在性能方面超过了CNN，但是其具有平方复杂度。经深入分析，ViT具有更加强大性能的原因在于：它利用了全局的感受野和动态的权重分配方法。因此，一种既具有ViT全局感知优势，又具有高计算效率的框架需要被提出。受到状态空间模型启发，我们提出了视觉状态空间模型（VMamba），这个模型能够在不破坏全局感受野的前提下，达到线性的计算复杂度。
mamba模型
最新发布
07-12
### Mamba 模型的技术原理 Mamba 是一种基于状态空间模型（State Space Model, SSM）的序列建模架构，其设计灵感来源于结构化状态空间模型的研究进展。与传统的递归神经网络（RNN）和Transformer不同，Mamba通过引入线性时不变（LTI）系统的概念，将序列建模问题转化为对状态空间的动态建模。在Mamba中，输入序列被映射到一个隐状态空间，并通过状态转移矩阵进行更新。这种设计允许模型以线性复杂度处理长序列，从而显著提升计算效率。 Mamba的核心技术包括： 1. **状态空间表示**：Mamba利用状态空间模型来捕捉序列数据的动态特性。其核心公式为： - 状态转移方程：$x_{t+1} = A x_t + B u_t$ - 输出方程：$y_t = C x_t + D u_t$ 其中，$x_t$是隐状态，$u_t$是输入，$y_t$是输出，而$A$、$B$、$C$、$D$是参数矩阵[^1]。 2. **选择机制**：Mamba引入了一个选择机制，通过可学习的参数调整状态转移矩阵$A$和输入矩阵$B$，使得模型能够动态地适应不同的输入序列。这一机制增强了模型的灵活性和表达能力。 3. **硬件感知优化**：Mamba的设计考虑了现代硬件的并行计算能力，通过优化矩阵运算和内存访问模式，实现了高效的训练和推理。 ### Mamba 的应用场景 Mamba模型因其高效的序列建模能力和灵活的设计，在多个领域展现出广泛的应用潜力： 1. **自然语言处理**：Mamba可以用于文本生成、机器翻译和文本摘要等任务。由于其线性复杂度的特点，Mamba在处理长文本时表现出色，尤其是在需要高效处理大规模数据的场景中。 2. **时间序列预测**：Mamba的状态空间模型天然适合时间序列建模，能够捕捉复杂的动态模式。它在金融预测、气象预测和工业监控等领域具有潜在的应用价值。 3. **语音识别与合成**：Mamba的线性复杂度和动态建模能力使其在语音处理任务中表现出色，尤其是在实时语音识别和高质量语音合成方面。 4. **生物信息学**：Mamba可以用于基因序列分析和蛋白质结构预测等任务，帮助研究人员更高效地处理大规模生物数据。 ### 相关论文与资源 1. **经典论文**： - **Mamba: A State Space Approach to Canonical Sequence Modeling**：这是Mamba模型的原始论文，详细介绍了其技术原理和设计思路。 - **Mamba-2: Enhancing the Efficiency and Flexibility of State Space Models**：该论文提出了Mamba-2，进一步优化了Mamba的性能和适用范围。 - **Structured State Space Models for Sequence Modeling**：这篇论文探讨了状态空间模型在序列建模中的应用，并为Mamba的设计提供了理论基础。 2. **开源实现与工具**： - **GitHub 项目**：https://github.com/Event-AHU/Mamba_State_Space_Model_Paper_List 提供了Mamba相关论文的列表以及实现代码。 - **PyTorch 实现**：许多研究者已经发布了基于PyTorch的Mamba实现，方便开发者快速上手和实验。 3. **社区与讨论**： - **学术会议**：Mamba相关的研究成果经常在顶级人工智能会议上展示，如NeurIPS、ICML和ICLR。 - **在线论坛**：Reddit和Stack Overflow等平台上有关于Mamba的讨论，用户可以分享经验或解决问题。 ### 示例代码 以下是一个简单的Mamba模型实现示例，展示了如何构建一个基本的状态空间模型： ```python import torch import torch.nn as nn class MambaModel(nn.Module): def __init__(self, input_dim, hidden_dim, output_dim): super(MambaModel, self).__init__() self.A = nn.Parameter(torch.randn(hidden_dim, hidden_dim)) self.B = nn.Parameter(torch.randn(hidden_dim, input_dim)) self.C = nn.Parameter(torch.randn(output_dim, hidden_dim)) self.D = nn.Parameter(torch.randn(output_dim, input_dim)) def forward(self, x): batch_size, seq_len, _ = x.shape hidden_state = torch.zeros(batch_size, self.A.shape[0], device=x.device) outputs = [] for t in range(seq_len): u_t = x[:, t, :] hidden_state = torch.matmul(hidden_state, self.A) + torch.matmul(u_t, self.B.t()) y_t = torch.matmul(hidden_state, self.C.t()) + torch.matmul(u_t, self.D.t()) outputs.append(y_t) return torch.stack(outputs, dim=1) # 示例用法 model = MambaModel(input_dim=10, hidden_dim=20, output_dim=5) input_data = torch.randn(32, 50, 10) # Batch size 32, sequence length 50, input dimension 10 output = model(input_data) print(output.shape) # 应该输出 (32, 50, 5) ```
评论 3
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值