一、为什么要用Mamba
在自然语言处理、时间序列分析等领域,序列建模一直面临着两大核心挑战:长距离依赖建模能力与计算效率。传统的循环神经网络(RNN)虽具备理论上的长序列处理能力,但由于梯度消失问题,实际有效建模长度通常局限在数百步;Transformer 通过自注意力机制实现了全局依赖建模,却付出了O(n2)O (n²)O(n2) 的时间复杂度代价,难以处理超长序列(如音频、基因组数据)。
Mamba(全称Mamba: A General Purpose Sequence Model)的出现打破了这一困境。作为一种基于状态空间模型(SSM) 的新型序列模型,Mamba 兼具以下核心优势:
- 线性时间复杂度:通过状态空间的递推特性,将序列处理复杂度降至 O(n)O (n)O(n),相比 Transformer 更适合处理数千甚至数万长度的序列。
- 长距离依赖建模能力:状态空间的动态演化机制可捕获序列中的长期依赖关系,理论上支持无限长度的上下文建模。
- 硬件加速友好:相比 RNN 的递归结构,Mamba 的矩阵运算更易利用 GPU/TPU 的并行计算能力,实现高效推理。
- 统一框架灵活性:可无缝兼容 CNN、RNN 等模型的特性,通过参数调整实现不同序列建模场景的适应性。
二、Mamba底层机制
2.1状态空间模型(State Space Model)(SSM)
状态空间模型起源于控制理论,其核心思想是将高阶动态系统分解为一阶状态方程的矩阵形式,便于分析与控制。以经典的弹簧振子系统为例,我们可以直观理解这一抽象过程:
例子引入:
一个弹簧振子系统如图所示:
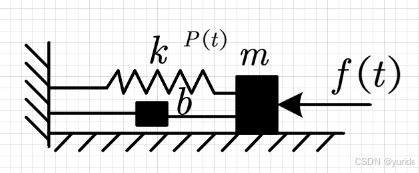
系统包含弹簧(弹性系数kkk)、质量块(质量 mmm)、阻尼器(阻尼系数 bbb),外力 f(t)f (t)f(t) 作用下,质量块位移 P(t)P (t)P(t) 满足二阶微分方程:
md2P(t)d(t)+bdP(t)dt+kP(t)=f(t)
m\frac{d^{2}P(t)}{d(t)}+b\frac{dP(t)}{dt}+kP(t)=f(t)
md(t)d2P(t)+bdtdP(t)+kP(t)=f(t)
令一阶状态变量h1(t)=P(t)(位移),h2(t)=dP(t)dt(速度)
令一阶状态变量h_1(t)=P(t)(位移),h_2(t)=\frac{dP(t)}{dt}(速度)
令一阶状态变量h1(t)=P(t)(位移),h2(t)=dtdP(t)(速度)
原式变为:
mh2(t)dt+bh2(t)+kh1(t)=f(t)
m\frac{h_2(t)}{dt}+bh_2(t)+kh_1(t)=f(t)
mdth2(t)+bh2(t)+kh1(t)=f(t)
h2(t)dt=1m(f(t)−bh2(t)−kh1(t))
\frac{h_2(t)}{dt}=\frac{1}{m}(f(t)-bh_2(t)-kh_1(t))
dth2(t)=m1(f(t)−bh2(t)−kh1(t))
用矩阵形式表示为:
d[h1(t))h2(t)]dt=[dh1(t)dtdh2(t)dt]=[01−km−bm][h1(t)h2(t)]+[01m]f(t)
\frac{d\begin{bmatrix}
h_1(t))\\h_2(t)
\end{bmatrix}}{dt}=\begin{bmatrix}
\frac{dh_1(t)}{dt}\\
\frac{dh_2(t)}{dt}
\end{bmatrix}=\begin{bmatrix}
0 &1 \\ -\frac{k}{m}
& -\frac{b}{m}
\end{bmatrix}\begin{bmatrix}
h_1(t)\\h_2(t)
\end{bmatrix}+\begin{bmatrix}
0\\\frac{1}{m}
\end{bmatrix}f(t)
dtd[h1(t))h2(t)]=[dtdh1(t)dtdh2(t)]=[0−mk1−mb][h1(t)h2(t)]+[0m1]f(t)
其中输出方程为
P(t)=[10][h1(t)h2(t)]
P(t)=\begin{bmatrix}
1&0
\end{bmatrix}\begin{bmatrix}
h_1(t)\\h_2(t)
\end{bmatrix}
P(t)=[10][h1(t)h2(t)]
我们可以观察到,原来的二阶的状态方程,通过转换变成一个一阶的矩阵表达,这个就是SSM的作用,其中h1(t))h_1(t))h1(t)),h2(t)h_2(t)h2(t)就称为状态。定义状态矩阵AAA输入矩阵BBB、输出矩阵CCC
A=[01−km−bm],B=[01m],C=[10]
A=\begin{bmatrix}
0 &1 \\ -\frac{k}{m}
& -\frac{b}{m}
\end{bmatrix},B=\begin{bmatrix}
0\\\frac{1}{m}
\end{bmatrix},C=\begin{bmatrix}
1&0
\end{bmatrix}
A=[0−mk1−mb],B=[0m1],C=[10]
f(t)f(t)f(t)其实就是整个系统的输入,P(t)P(t)P(t)其实就是整个系统的输出,我们引入到神经网络中,做一个替换,使得x(t)=f(t)x(t)=f(t)x(t)=f(t),y(t)=P(t)y(t)=P(t)y(t)=P(t),同时令h(t)=[h1(t))h2(t)]h(t)=\begin{bmatrix}
h_1(t))\\h_2(t)
\end{bmatrix}h(t)=[h1(t))h2(t)],则连续时间下的 SSM 可表示为:
dh(t)dt=Ah(t)+Bx(t)
\frac{dh(t)}{dt}=Ah(t)+Bx(t)
dtdh(t)=Ah(t)+Bx(t)
y(t)=Ch(t)
y(t)=Ch(t)
y(t)=Ch(t)
我们就可以得到了Mamba论文中的第一个公式的推导过程。但是我们可以看到上面的系统是基于一个连续的系统,而我们的神经网络的构建过程是一个离散化的过程,因此需要将连续 SSM 转换为离散形式。Mamba 采用零阶保持法(Zero-Order Hold, ZOH),其核心思想是在离散时间间隔内假设输入值保持不变(如x(tk)x(t_k)x(tk)在区间[tk,tk+1][t_k, t_{k+1}][tk,tk+1]内恒定)。具体如下图所示:
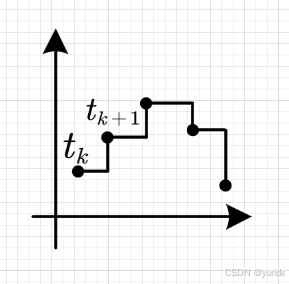
为了实现离散化过程,我们在等式两边同时乘e−Ate^{-At}e−At等式变为:
e−Atdh(t)dt=e−AtAh(t)+e−AtBx(t)
e^{-At}\frac{dh(t)}{dt}=e^{-At}Ah(t)+e^{-At}Bx(t)
e−Atdtdh(t)=e−AtAh(t)+e−AtBx(t)
e−Atdh(t)dt−e−AtAh(t)=e−AtBx(t)
e^{-At}\frac{dh(t)}{dt}-e^{-At}Ah(t)=e^{-At}Bx(t)
e−Atdtdh(t)−e−AtAh(t)=e−AtBx(t)
接着我们可以发现其实
de−Ath(t)dt=e−Atdh(t)dt−e−AtAh(t)
\frac{de^{-At}h(t)}{dt}=e^{-At}\frac{dh(t)}{dt}-e^{-At}Ah(t)
dtde−Ath(t)=e−Atdtdh(t)−e−AtAh(t)
那么我们的等式变为:
de−Ath(t)dt=e−AtBx(t)
\frac{de^{-At}h(t)}{dt}=e^{-At}Bx(t)
dtde−Ath(t)=e−AtBx(t)
我们对两边同时求积分可以得到:
∫tktk+1de−Ath(t)dt=∫tktk+1e−AtBx(t)dt
\int_{t_{k}}^{t_{k+1}} \frac{de^{-At}h(t)}{dt}=\int_{t_{k}}^{t_{k+1}}e^{-At}Bx(t)dt
∫tktk+1dtde−Ath(t)=∫tktk+1e−AtBx(t)dt
由于在零阶保持法中,x(t)x(t)x(t)是一个与ttt无关的常量,且用tkt_ktk的状态来表示,因此在积分中可以直接提取出来因此我们的积分可以进一步简化为:
e−Ath(t)∣tktk+1=∫tktk+1e−AtdtBx(tk)
e^{-At}h(t)|_{t_k}^{t_{k+1}}=\int_{t_k}^{t_{k+1}}e^{-At}dtBx(t_k)
e−Ath(t)∣tktk+1=∫tktk+1e−AtdtBx(tk)
e−Atk+1h(tk+1)−e−Atkh(tk)=−1Ae−Atk∣tktk+1Bx(tk)
e^{-At_{k+1}}h(t_{k+1})-e^{-At_{k}}h(t_{k})=-\frac{1}{A}e^{-At_{k}}|_{t_k}^{t_{k+1}}Bx(t_k)
e−Atk+1h(tk+1)−e−Atkh(tk)=−A1e−Atk∣tktk+1Bx(tk)
e−Atk+1h(tk+1)=e−Atkh(tk)−1Ae−Atk∣tktk+1Bx(tk)
e^{-At_{k+1}}h(t_{k+1})=e^{-At_{k}}h(t_{k})-\frac{1}{A}e^{-At_{k}}|_{t_k}^{t_{k+1}}Bx(t_k)
e−Atk+1h(tk+1)=e−Atkh(tk)−A1e−Atk∣tktk+1Bx(tk)
e−Atk+1h(tk+1)=e−Atkh(tk)−1Ae−Atk+1Bx(tk)+1Ae−AtkBx(tk)
e^{-At_{k+1}}h(t_{k+1})=e^{-At_{k}}h(t_{k})-\frac{1}{A}e^{-At_{k+1}}Bx(t_k)+\frac{1}{A}e^{-At_{k}}Bx(t_k)
e−Atk+1h(tk+1)=e−Atkh(tk)−A1e−Atk+1Bx(tk)+A1e−AtkBx(tk)
等式两边同时乘以eAtk+1e^{At_{k+1}}eAtk+1可以得到:
h(tk+1)=eA(tk+1−tk)h(tk)−1ABx(tk)+1AeA(tk+1−tk)Bx(tk)
h(t_{k+1})=e^{A(t_{k+1}-t_k)}h(t_{k})-\frac{1}{A}Bx(t_k)+\frac{1}{A}e^{A(t_{k+1}-t_{k})}Bx(t_k)
h(tk+1)=eA(tk+1−tk)h(tk)−A1Bx(tk)+A1eA(tk+1−tk)Bx(tk)
令tk+1−tk=Δt_{k+1}-t_k=\Deltatk+1−tk=Δ
h(tk+1)=eAΔh(tk)−1ABx(tk)+1AeAΔBx(tk)
h(t_{k+1})=e^{A\Delta }h(t_{k})-\frac{1}{A}Bx(t_k)+\frac{1}{A}e^{A\Delta }Bx(t_k)
h(tk+1)=eAΔh(tk)−A1Bx(tk)+A1eAΔBx(tk)
进一步化简为:
h(tk+1)=eAΔh(tk)+A−1(eAΔ−1)Bx(tk)
h(t_{k+1})=e^{A\Delta }h(t_{k})+A^{-1}(e^{A\Delta }-1)Bx(t_k)
h(tk+1)=eAΔh(tk)+A−1(eAΔ−1)Bx(tk)
令Aˉ=eAΔ,Bˉ=A−1(eAΔ−1)B\bar{A}=e^{A\Delta },\bar{B}=A^{-1}(e^{A\Delta }-1)BAˉ=eAΔ,Bˉ=A−1(eAΔ−1)B
代入得:
h(tk+1)=Aˉh(tk)+Bˉx(tk)
h(t_{k+1})=\bar{A}h(t_{k})+\bar{B}x(t_k)
h(tk+1)=Aˉh(tk)+Bˉx(tk)
我们就得到了第二个离散化的公式。
2.2 Mamba对时变系统的核心改进:从固定参数到动态适应
在传统状态空间模型中,离散化后的参数Aˉ\bar{A}Aˉ和Bˉ\bar{B}Bˉ由系统固有属性(如弹簧振子的质量、阻尼系数)决定,属于时不变参数。但实际序列数据(如语音、金融时序)常呈现时变特性(即系统动态特性随时间变化),例如:
- 语音信号中不同频段的能量分布随发音时刻变化;
- 金融市场中资产相关性受突发事件影响而波动。
Mamba在保留基础矩阵AAA固定性的前提下,通过动态调节其他参数实现时变适配,将状态转移方程重构为:
h(tk+1)=Ah(tk)+Btx(tk)
h(t_{k+1}) = A h(t_k) + B_t x(t_k)
h(tk+1)=Ah(tk)+Btx(tk)
y(tk)=Cth(tk)
y(t_k) = C_t h(t_k)
y(tk)=Cth(tk)
其中AAA为固定基础矩阵,BtB_tBt、CtC_tCt为动态参数,Δt\Delta_tΔt为时变离散化步长,以下是各参数的数学机制解析:
对AAA的解释说明
在传统时不变框架下,AAA作为核心状态转移算子,其参数刻画系统固有动态,如物理系统中惯性、阻尼主导的状态演化规律,一旦离散化确定便保持恒定,无法响应序列数据的时变特性。而在适配时变系统的改进逻辑里,AAA虽仍承载基础状态传播的 “默认规则”,但需与其他动态模块协同,为BtB_tBt、ΔtΔ_tΔt等时变调节提供稳定的状态演化基底。其固定性成为时变适配的 “基准参考系”—— 如同物理定律恒定不变,却能通过外力(时变参数)调节系统输出。这种设计保障状态空间模型在动态调整中仍具备可追溯的核心运算逻辑,避免因过度时变导致状态演化失序。例如,在语音处理中,AAA可预设为捕捉声波传播的基础动力学,而时变参数负责适配不同发音时刻的特征变化。
对BtB_tBt的解释说明
BtB_tBt作为时变输入映射算子,数学表达式为:
Bt=Project(σ(St)⊗Bˉ)
B_t = \text{Project}(\sigma(S_t) \otimes \bar{B})
Bt=Project(σ(St)⊗Bˉ)
其中:
- St=Ws⋅[h(tk);x(tk)]S_t = W_s \cdot [h(t_k); x(t_k)]St=Ws⋅[h(tk);x(tk)](状态-输入联合特征);
- σ(⋅)\sigma(\cdot)σ(⋅)为激活函数(如Sigmoid),实现输入权重动态筛选;
- ⊗\otimes⊗表示元素级乘法,Project(⋅)\text{Project}(\cdot)Project(⋅)为线性投影矩阵。
BtB_tBt作为时变输入映射算子,突破传统固定Bˉ\bar{B}Bˉ的限制,依据时刻ttt的序列数据特征动态调整。面对语音序列,它可感知不同发音时刻频段能量分布差异,适配调制输入与状态的耦合强度;针对金融时序,能捕捉突发事件冲击下资产相关性波动,实时重塑新信息向状态空间的注入方式。通过与选择机制(Selection Mechanism)、投影(Project)模块联动,BtB_tBt实现输入信息的时变筛选与加权投影,让状态更新精准响应数据的瞬时动态,成为模型适配时变特性的 “输入动态调节器” 。
对CtC_tCt的解释说明
CtC_tCt通过动态解耦状态表征生成输出,数学形式为:
Ct=MLP(h(tk))⋅Cbase
C_t = \text{MLP}(h(t_k)) \cdot C_{\text{base}}
Ct=MLP(h(tk))⋅Cbase
其中:
- CbaseC_{\text{base}}Cbase为固定基础输出矩阵(如弹簧振子系统中C=[1,0]C=[1,0]C=[1,0]);
- MLP(⋅)\text{MLP}(\cdot)MLP(⋅)为多层感知机,根据当前状态h(tk)h(t_k)h(tk)生成时变调节权重。
CtC_tCt作为时变输出映射算子,区别于传统固定输出映射,需适配状态空间因时变调整后的内部表征。在时变系统中,随AAA主导的状态演化、BtB_tBt驱动的输入融入,状态空间的信息分布持续动态重构,CtC_tCt需实时解耦状态特征,生成贴合当前时刻数据特性的输出yty_tyt
对Δt\Delta_tΔt的解释说明
Δt\Delta_tΔt为时变离散化步长,计算逻辑为:
Δt=Discretize(vt,Δmin,Δmax)
\Delta_t = \text{Discretize}(v_t, \Delta_{\text{min}}, \Delta_{\text{max}})
Δt=Discretize(vt,Δmin,Δmax)
其中:
- vt=∥∇x(tk)∥2v_t = \|\nabla x(t_k)\|_2vt=∥∇x(tk)∥2(输入信号变化率);
- Discretize(⋅)\text{Discretize}(\cdot)Discretize(⋅)为分段函数:
Δt={Δminvt>τΔmaxvt<ϵΔbase+β⋅vtotherwise \Delta_t = \begin{cases} \Delta_{\text{min}} & v_t > \tau \\ \Delta_{\text{max}} & v_t < \epsilon \\ \Delta_{\text{base}} + \beta \cdot v_t & \text{otherwise} \end{cases} Δt=⎩⎨⎧ΔminΔmaxΔbase+β⋅vtvt>τvt<ϵotherwise
Δt\Delta_tΔt作为时变离散化调节算子,打破传统固定离散化步长 / 参数的设定。在时变系统中,序列数据的动态变化速率、特征尺度存在瞬时差异,Δt\Delta_tΔt通过感知时刻ttt的数据时变特性(如语音信号的节奏变化、金融时序的波动频率),动态调整离散化策略。
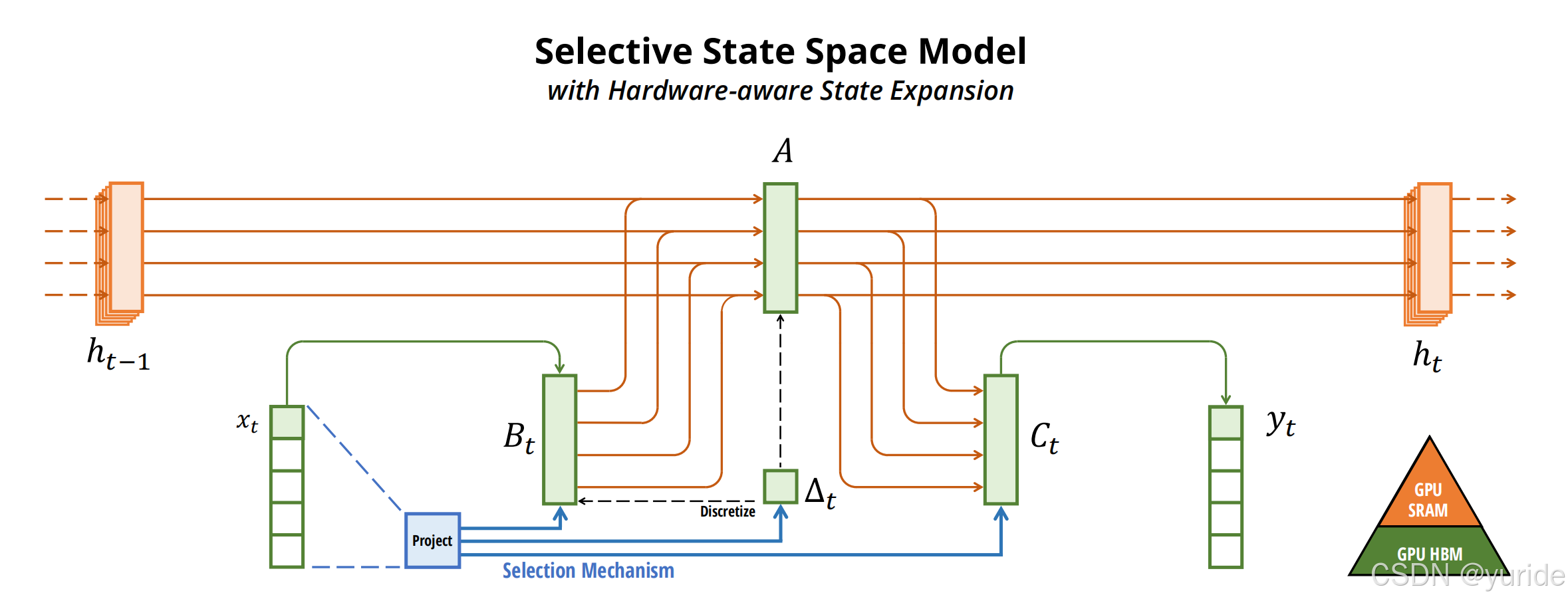
综上所述,我们得到下面的mamba的算法图:























 4568
4568

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








