14.火柴棒等式

题目描述

给你n根火柴棍，你可以拼出多少个形如 $A+B=C$ 的等式？等式中的 $A$、$B$、$C$ 是用火柴棍拼出的整数（若该数非零，则最高位不能是 $0$）。用火柴棍拼数字 $0\sim9$ 的拼法如图所示：


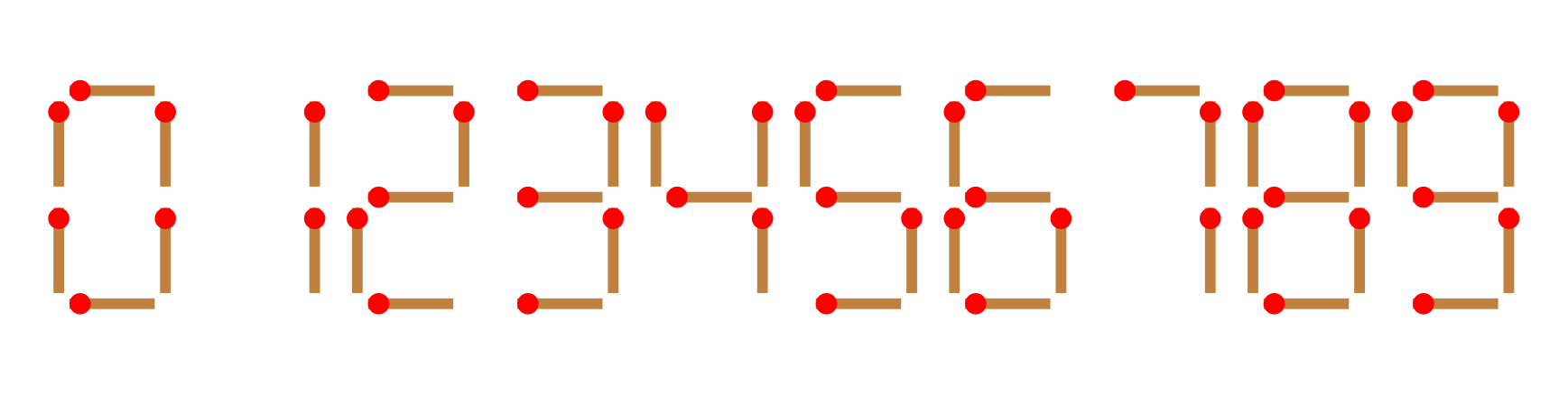
注意：

1. 加号与等号各自需要两根火柴棍；
2. 如果 $A\neq B$，则 $A+B=C$ 与 $B+A=C$ 视为不同的等式（$A,B,C\geq0$）；
3. $n$ 根火柴棍必须全部用上。

## 输入格式

一个整数 $n(1 \leq n\leq 24)$。

## 输出格式

一个整数，能拼成的不同等式的数目。

## 输入输出样例 #1

### 输入 #1

```
14
```

### 输出 #1

```
2
```

## 输入输出样例 #2

### 输入 #2

```
18
```

### 输出 #2

```
9
```

## 说明/提示

【输入输出样例 1 解释】

$2$ 个等式为 $0+1=1$ 和 $1+0=1$。

【输入输出样例 2 解释】

$9$ 个等式为

$0+4=4$、$0+11=11$、$1+10=11$、$2+2=4$、$2+7=9$、$4+0=4$、$7+2=9$、$10+1=11$、$11+0=11$。

noip2008 提高第二题

 

#include<bits/stdc++.h>
using namespace std;
const int N=10010;

int n;
int firenums[N]={6,2,5,5,4,5,6,3,7,6};
int arr[N];
int res=0;
int col(int x)
{
    if(firenums[x]) return firenums[x];
    else{
        int firenum=0;
        while(x)
        {
            firenum+=firenums[x%10];
            x/=10;
        }
    return firenum;
    }
}
void dfs(int x,int sum) //遍历到哪个位置
{
    if(sum>n) return;
    if(x>3)
    {
        if(arr[1]+arr[2]==arr[3]&&sum==n)
        {
            res++;
        }
        return;
    }

    for(int i=0;i<=1000;i++)
    {
        arr[x]=i;
        dfs(x+1,sum+col(i));
        arr[x]=0;
    }
}
int main()
{
    cin>>n;
    n-=4;
    dfs(1,0);
    cout<<res;
    return 0;
}

总结思考：

        dfs的题目，考虑用一个数组来存放每个数字对应的木柴数量，之后>9的数字需要用函数计算所需的木柴数量；

        开始遍历的要注意恢复现场；进行减枝操作，如果sum>n，直接退出