Consensus explained

Making comparisons between currencies and blockchain systems is often a bad idea. Why? Because they’re different solutions to different problems. All systems are based on their own security models. If we’re talking about decentralized systems, and keep that ‘decentralized’ idea front of mind, then the most important thing that’s worth mentioning is consensus. Of course, there are many kinds of consensus, of which the two most popular types are known as PoW (Proof of Work) and PoS (Proof of Stake). People also often claim that one kind of consensus is better than another — but here, again, there are different solutions which fit different situations. Even so, it’s clear that within one kind, there could be better or worse options. There’s been very little written about when it’s better to deploy a particular kind of consensus — which helps foster the misconception that you can take bitcoin’s or Ethereum’s codebase — and just use it for your own use-case? And there’s even less written about how to classify kinds of consensus.

In practice, this leads to situations when someone plans designing a national digital currency, they use a bitcoin fork as the template (I’ve come across such cases :) ). In this case it’s not clear who the miners are, or why we even need them.

Let’s look at a different example. Some people call Ripple a centralized blockchain. In fact they’re right, in the case of a specific company which controls the validators network — although wrong when referring to the underlying technology.

Another example is a case of ‘private blockchains’ (I believe it’s a mistaken term — but I’m forced to use it, otherwise people are going to get disoriented) that community doesn’t like. People say that they are centralized, insecure, don’t differ in any way from MySQL etc. Yet again, in the majority of cases this isn’t fair — it’s just that the system-builder never explained the security model, and critics didn’t dig deeper.

At this point I’ll try to explain what issue is solved by each consensus — in the plainest language I can muster.

1. Multisignature/Byzantine Fault Tolerance (BFT). These algorithms are primarily used for achieving consensus among a limited group of people (In the case of multisignature between few participants — or in the case of BFT, between dozens of them, most usually equals). It makes sense to use BFT when all the parties in the process know each other, and the list of them doesn’t change often. One example would be voting among the inhabitants of a building on collectively-organized repairs.

2. Proof of Stake (PoS) — voting by stake (or by percentage of ownership). This is very similar to voting among shareholders in a company — whoever holds the largest slice of the pie will get the most say on how decisions are made. The specific quorum for achieving consensus can vary depending on the company. Some may require a simple majority (51%), others might demand a two-thirds majority, and there could even be those who require a unanimous 100%. Other consensuses in the class are PoI (proof of importance) and DPoS(delegated proof of stake, when small-scale shareholders choose a delegate as their representatives).

3. Federated Byzantine Agreement (FBA), which was first introduced by Ripple, and then formally proven by Stellar, permits reaching consensus among large numbers of participants who don’t know each other personally, and in situations when the total number of participants may not even be known. Each participant extends to trust to only a limited (by number) group of other participants, and therefore achieves consensus only amongst a narrow circle. However, since each of these circles has some element of overlap with others, it’s possible to achieve overall consensus. There are not, however, many examples of such situations in real life — models might include sowing the seeds of revolution, when people spread the word mouth-to-mouth, and infect others with their enthusiasm.

4. Proof of work (PoW) owes its popularity to cryptocurrencies, and is certainly the most complicated to explain. In PoW, all of the participants remain anonymous, don’t extend trust to each other, and their total number is unlimited/unknown.

Imagine if team of warriors, instead of fighting with each other for trophies after each battle are comparing their weapons — and decisions would be taken on the basis of the comparison. So to define who deserves trophies warriors are challenging a goal — let’s say a dragon. Whoever has the greater fire-power will win most often — and thus will most often will take the reward. All of the participants will be working on building up their strength before battles— and this can lead to an ‘arms race’. Obviously, it’s possible for a part or section of the participants to opt to leave entirely, and set up their own separate squad (in other words, a ‘fork’).

If we try to classify all these forms of consensus, there are two primary criteria (but there could perhaps be other ways of classifying them), and these are (i) the anonymity of each validator, and (ii) lever of trust to a specific validator (more thoughts here).

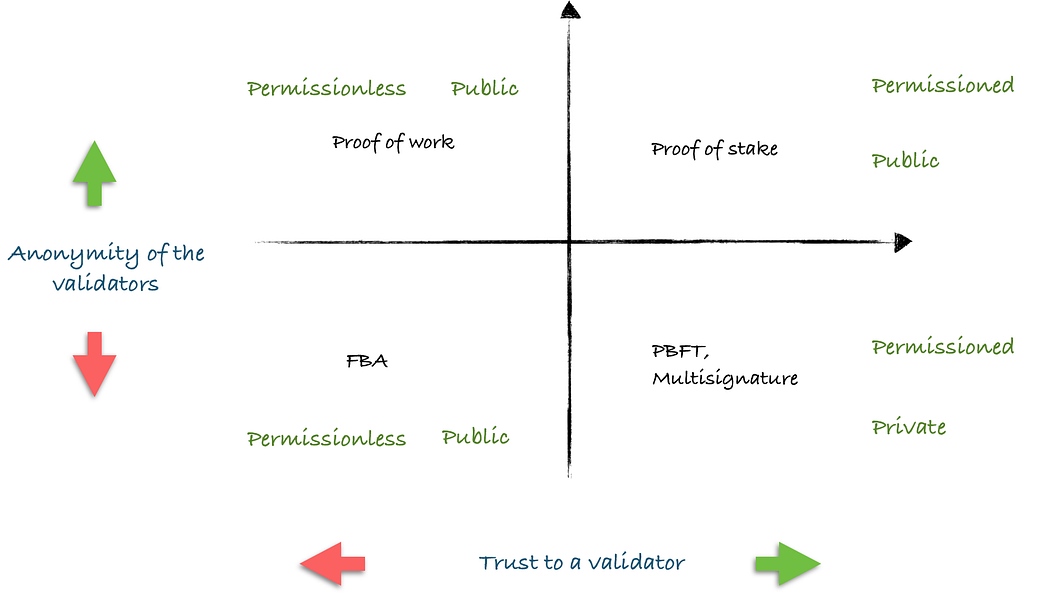
Now it would make sense to compare systems within groups. Of course, there will also be some subgroups — but at least there won’t be utter confusion.

Visit http://tokend.org/ to know more about Distributed Lab’s approach to standardize development of tokenization systems.

https://medium.com/@pavelkravchenko/consensus-explained-396fe8dac263