停电期间的电动汽车优先级与功率分配:一种基于字典序方法的多目标优化方法
摘要
电动汽车(EV)数量的增长导致交通对电力行业的依赖性增加。在停电期间,特别是长时间停电时,本地可用能量可能不足以满足所有电动汽车的能量需求。因此,本研究提出了一种多准则电动汽车优先级分配方案,以在停电期间公平地向电动汽车分配可用能量。所考虑的五个主要优先级因素包括出行目的、电动汽车乘员、能量缺口、出发时间和用户行为。基于这五个优先级因素的不同组合,分别针对社会福利、社区福祉以及电动汽车车主的个体满意度构建了三个指标。在此基础上,建立了一个基于这三个指标的多目标优化问题,以将可用功率优先分配给指标值较高的电动汽车。采用字典序方法求解该多目标优化问题,该方法相较于传统使用的加权和法和ɛ‐约束法具有更优的性能。所提出的方法对各个目标函数的权重不敏感,并能够处理多个优先级层次。为了量化结果,针对三个参数(社会福利、社区福祉和个体满意度)分别定义了服务百分比和未服务指数,并将所提出方法的结果与加权和法及ɛ‐约束法的结果进行了比较。此外,还对不同不确定因素进行了敏感性分析,包括电动汽车数量、电动汽车需求不确定性、可再生能源功率不确定性以及电池荷电状态估计误差。仿真结果表明,所提出的方法在停电期间向电动汽车分配功率方面具有优越性。
索引术语 —电动汽车,公平性,字典序方法,多目标优化,功率分配,停电。
I. 引言
交通运输电气化正变得越来越可行,这得益于电池成本的降低以及电动汽车(EVs)生产规模的扩大。预计电动汽车将与传统汽车具有同等竞争力,在不久的将来[1]。电动汽车有望通过减少交通领域对基于化石燃料的能源的消耗,从而降低温室气体排放[1]。
然而,电动汽车渗透率的提高可能因不确定负荷增加而导致电力可靠性和质量问题[2],[3]。这些问题可通过采用智能充电技术[4]、在充电站集成储能系统[5]以及升级配电/输电网络(作为最后手段)[6]来解决。此外,电动汽车渗透率的提高也增强了交通与电力网络的相互依赖性[7]。由于交通领域对电力的依赖性增加,在停电期间该问题会变得更加严重。
A. 交通电气化与电力中断
同时,由于气候变化[8],[9],电力系统中的停电事件(特别是与天气相关的事件)在规模和频率上都在增加。例如,2014年至2018年美国重大停电的平均次数是1980年至2018[10]年间极端事件平均次数的两倍以上。这些重大事件导致数百万用户断电,停电时间延长,并造成巨大的经济损失。[10],[11]中列出了近年来全球重大停电事件的历史概览。其中一些事件包括2008年中国冰暴、2011年日本地震、2013年德国暴雨和洪水、2016年澳大利亚风暴、2016年中国江苏省龙卷风、2017年美国哈维飓风以及2015年加拿大风暴。据[8]报道,仅2017年一年全球就发生了九起重大停电事件,每次事件至少影响25万用户。此外,一些与技术故障和网络攻击相关的重大停电也导致了大停电,例如2015[10],乌克兰的网络攻击、2017[8],台湾发电厂故障、2019[10],6月南美洲的网络攻击以及2019[10]8月印度尼西亚的网络攻击。
因此,在不久的将来,任何自然灾害或人为事件导致的停电都会对交通领域产生重大影响。停电期间电动汽车的管理是与电动汽车韧性相关的主要问题之一,但目前却未受到足够关注[5],[12]。在紧急情况下,由于有限的本地资源,可能无法满足所有电动汽车的电力需求。因此,需要建立电动汽车优先级和可用能量分配机制,以增强电动汽车车主之间的公平性。
B. 公平性与电动汽车的功率分配
在不同申领者之间分配稀缺资源一直是各个领域的活跃研究方向,文献中已提出了多种方法。按比例分配被认为是最古老且应用最广泛的方法[13],即根据每个申领者的申领数量来分配稀缺资源。经济学领域为破产问题[13],[14]提出了若干规则,例如塔木德规则、等量分配规则、等量损失规则等,这些规则在不同领域中被广泛应用。然而,这些规则无法确保索赔者之间的公平性,要么偏向大索赔者,要么偏向小索赔者,可能导致不同索赔者拒绝接受所提出的解决方案。因此,许多学科中都考虑了公平导向的稀缺资源分配规则[15]‐[20]。在[15]中,水资源分配被视为一个多目标优化问题,并采用了可衡量的公平规则来在不同索赔者之间进行水资源分配。在[16],[17]中,针对紧急情况下患者之间稀缺医疗资源的分配,考虑了不同的福祉与公平规则。在[18]中,提出了基于努力的激励机制以提高对等系统的公平性。在电力系统中,已考虑在资源匮乏地区[19]或应急时期[20]公平地进行减载分配。
在不同的研究中[21]‐[23],也考虑了客户的意愿和偏好,以向电动汽车分配电力。在[21]中考虑了电动汽车聚合商在考虑电动汽车驾驶员延迟充电意愿的同时实现利润最大化的问题,而[22]则关注用户体验舒适度。在[23]中考虑了用户偏好和充电标准,并根据用户对风险和收益的敏感性将其分为三组。
对于电动汽车而言,为到达目标目的地,电动汽车需要获得特定数量的电量,低于所需电量的供电是不可接受或无意义的。因此,上述稀有资源分配方法(如比例分配或破产规则)无法直接应用于电动汽车功率分配问题。相反,可以通过对电动汽车进行优先级排序,并以公平性为导向进行功率分配,从而获得有意义的结果。此外,由于在对电动汽车进行优先级排序时考虑了多种因素,而不仅仅是所需电量,因此以公平性为导向的功率分配将更容易被所有用户接受。因此,近年来已开展了多项关于系统拥塞或过载期间以公平性为导向的电动汽车充电研究[24]‐[29]。
在[24]中考虑了电动汽车的可用能量和所需能量以及电动汽车用户的离开时间和停留时间,以在电网拥堵期提高公平性。类似地,在[25]中分析了不同优先级标准的影响,例如电动汽车的荷电状态(SOC)、充电松弛时间和已分配能量。在[26]中提出了最小松弛比方法,该方法优先服务相对于其剩余服务时间具有最紧急截止时间的电动汽车。结果表明,与著名的比例规则相比,该方法在系统过载期间能够更公平地分配功率。在[27]中,根据请求相同能量的电动汽车在市场价格变化上的差异来量化不公平性,并提出了一种最小化不公平性的方法。为了在电动汽车之间公平利用电网容量,在[28]中提出了加法递增乘法递减方法,并仅使用本地测量来决定电动汽车的充电功率。在[29]中考虑了在有限容量下电动汽车之间的功率共享公平性,同时遵守欠压和变压器过载限制。在[29]中提出了一种基于流体模型的排队方案,并将其与物理开始时间公平排队方案进行了比较。
C. 现有研究的局限性与研究贡献
从文献综述中可以发现,关于系统过载期间(即并网模式下)以公平性为导向的电动汽车优先级排序已有大量研究。因此,这些现有研究的重点在于最小化等待时间[24],[25],[28]和/或最大化个体满意度[20],[24],[27]。然而,这些研究并未考虑社会福利和社区福祉。但在停电期间,这两个参数(社会福利和社区福祉)变得至关重要。
由于不同电动汽车车主的出行目的、电动汽车乘员以及任务紧急程度可能各不相同,因此我们认为,仅以个体满意度作为衡量标准不足以评估向不同电动汽车分配电力的公平性。例如,一对夫妇进行休闲活动、一名成年人参与应急响应以及一位老年人前往医院的出行目的各不相同,尽管这三类电动汽车车主的个体满意度可能相同,但当选择其中一辆电动汽车供电时,所产生的社会福利以及个体/社区福祉将显著不同。此外,系统过载与紧急情况下的问题性质存在一些根本性差异:1)系统高峰时段是已知的,用户可避开这些时段,而重大停电的发生或恢复时间则无法准确预测;2)在系统过载情况下,所有电动汽车的能源需求均可满足,仅部分电动汽车会经历一定的时间延迟;但在紧急情况下,由于电力供应有限以及停电事件持续时间较长(尤其是在自然灾害中),部分电动汽车的需求可能完全无法满足;3)系统高峰时段通常仅为数小时,用户可提前储存电能,而停电持续时间可能从几小时到数天不等,使得长期储电几乎不可能实现。因此,有必要根据可用功率的数量,对电动汽车实施多准则优先级索引,并优先为具有最高指标的电动汽车分配电力。
随着电动汽车渗透率的提高以及电动汽车数量超过传统内燃机车辆,未来对特定电动汽车进行电力分配决策将变得更加重要。在不久的将来,电动汽车将被用于各种用途,包括紧急情况响应、公共交通和个人使用等。在停电期间,由于电动汽车数量增加且用途多样,对不同电动汽车进行电力分配的决策不可避免。因此,本研究试图克服现有研究的局限性。与现有研究相比,本研究的主要贡献如下。
与现有研究主要关注电网的正常运行(过载)不同,本研究考虑了停电期间向电动汽车分配功率的问题。据作者所知,本研究首次提出了在重大停电(以韧性为导向的事件)期间向电动汽车进行功率分配的方法。
- 为了优先分配电力给电动汽车,本研究提出了一种以公平为导向的多标准优先级方案。通过考虑出行目的、电动汽车乘员、SOC差距、出发时间和用户行为,为每辆电动汽车制定了社会福利、社区福祉以及个体满意度指标。
- 为了有效解决多目标问题,本研究采用了基于字典序方法的求解方案。所采用方法的性能与常用于求解多目标问题的方法(如加权和法以及epsilon‐约束法)进行了比较。
- 最后,为了分析所提出的方法的性能,进行了多个测试用例的仿真。此外,还分析了可再生能源功率的不确定性、SOC估计误差、电动汽车渗透率以及所需能量的不确定性对所提出的方法性能的影响。
II. 网络配置与提出的指标
公平性的认知在不同学科中可能有所不同,也可能随着当前情况的变化而变化。例如,在医院中,正常情况下所有患者住院的平等机会被视为公平,但在紧急情况下,禁止病情较轻的患者住院将被认为是公平的。本研究中,电动汽车车主的公平性被定义为根据电动汽车对社区和个人的相对重要性(优先级)来分配电力。由于本研究的重点是重大停电(紧急情况)期间的电力分配,因此基于优先级的分配相比对所有电动汽车进行平等分配将被视为更公平。本研究的主要贡献在于定义了考虑多种因素的电动汽车相对重要性(优先级)指标,并有效解决了该问题,即采用字典序方法。本节讨论了网络配置以及用于电动汽车优先级确定所考虑的因素。
A. 网络配置
本研究的重点是在停电期间(即孤岛模式下)为电动汽车分配电力。由于与公用电网断开连接,在紧急情况下只能使用本地电力资源。如图1所示,这些本地资源可以是可再生能源、储能系统和小型微型涡轮机。所有注册到特定充电站的电动汽车都会被分配一个编号(ID)。所有电动汽车将向管理系统报告其所需的电量以及有关多个因素的信息,管理系统根据这些因素对电动汽车进行优先级排序。这些因素的详细信息将在下一节中讨论。
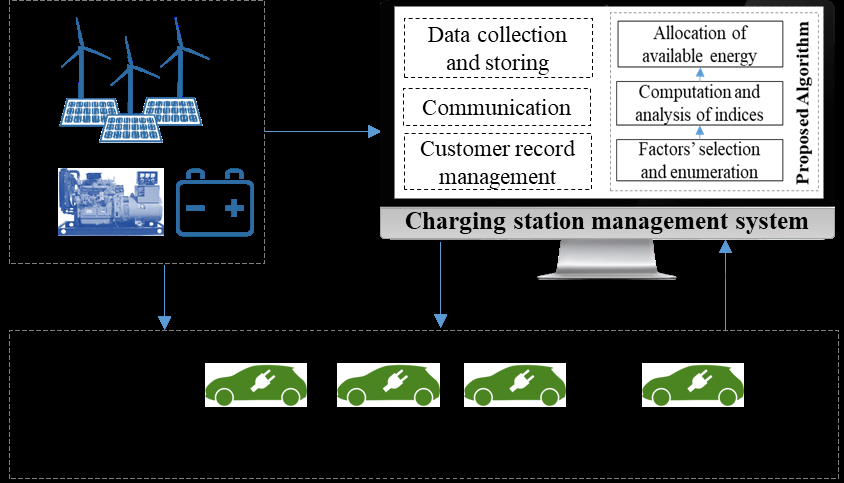
充电站管理系统配备了用于电动汽车优先级和功率分配的 proposed algorithm。该 proposed algorithm 从能源接收可用功率信息,同时从请求充电的电动汽车接收能量需求和因素信息。
该时间段内的充电。所提出的算法根据可用信息对所有电动汽车进行优先级排序,并从优先级最高的电动汽车开始分配可用功率。分配给每辆电动汽车的功率由充电站管理系统告知,而该能量(总能量)由能源提供。
B. 电动汽车优先级考虑的因素
在本研究中,考虑了五个主要因素来确定电动汽车车主的社会福利、社区福祉以及个体满意度,具体如下。
-
出行目的 :它决定了电动汽车请求充电的出行目标。出行目的将包含多个离散选项,电动汽车车主必须选择其中一项。这些选项可以包括休闲活动、社会服务、工作/学习、应急响应、居家购物和就医等。充电站管理系统将为每种出行目的设定相应的评分,例如应急响应的评分最高,而休闲活动的评分最低。这些评分可在预定义量表上进行分配,例如 $[1..\psi, ..\omega, ..K]$,其中1为最低值,K为最高值。数值越接近1表示重要性越低,越接近K表示重要性越高。$\psi$ 是较低重要性任务的阈值,低于此阈值的用户(如休闲活动)无法使用某些出发时间选项(越快越好),相关内容将在后续章节中讨论。类似地,$\omega$ 是较高重要性任务的阈值,高于此阈值的用户(如应急响应)在电动汽车乘员方面无法选择某些选项,例如残疾人或携带儿童等。当存在多个出行目的时,将以最高优先级的出行为准。出行目的信息将有助于确定社会福利和社区福祉,相关内容将在下一节中讨论。然而,仅凭出行目的不足以确定向特定电动汽车分配电力的公平性。
-
电动汽车乘员 :表示请求充电的电动汽车上的乘员。与出行目的类似,它也包含若干离散选项,电动汽车车主需选择其中一项。这些选项可以包括老年人、残疾人、正常成年人和携带儿童等。在存在多种乘员类型的情况下,将选择对应数值最高的电动汽车乘员类型。然而,存在一些根据出行目的对电动汽车乘员施加约束。例如,用于应急响应的电动汽车乘员只能是正常成年人,如公式(1)所示。这意味着,如果出行目的因素($\alpha_{tp}$)大于某一阈值($\omega$),则电动汽车乘员因素($\alpha_{eo}$)只能取对应特定类别($\beta$)的值,即正常成年人。这表明,执行应急响应任务的电动汽车不能选择老年人、携带儿童或残疾人作为乘员。同样,以社会服务为出行目的的电动汽车不能选择残疾人或携带儿童。然而,这些并非固定参数,政策制定者可以选择 $\omega$ 的任意取值,并相应地制定指标。该因素还有助于确定社会福利和社区福祉。
$$
\alpha_{tp} > \omega \rightarrow \alpha_{eo} = \beta \quad (1)
$$ -
SOC差距 :它表示vth EV中当前可用能量与该电动汽车完成目标任务所需能量之间的差距。能量缺口越大,评分越低;反之亦然。此因素可用于确定社会福利、社区福祉以及个体满意度。如果两辆电动汽车具有相同的出行目的和电动汽车乘员,则SOC差距较小的电动汽车将被优先考虑。这将一方面减少充电时间,另一方面增加被服务的电动汽车数量,即分别为2辆电动汽车分配10千瓦时能量,而不是为一辆电动汽车分配20千瓦时能量。公式(2)用于计算对应于该电动汽车所需能量的SOC差距因素($\alpha_{sg}$)。$E_{cap}$ 是电动汽车中电池的容量,$\delta_{max}$ 是一个归一化因子,用于使其处于其他因素的范围内。$E_{req}$ 是一个随机变量,将在后续章节中讨论。
$$
\alpha_{sg} = (E_{cap} - E_{req}) / \delta_{max} \quad (2)
$$ -
出发时间 :表示电动汽车期望完成充电并启程前往目标任务的时间,即任务的紧急程度。该选项将包含若干离散选项,电动汽车车主必须从中选择其一。这些选项可以是尽快(ASAP)、在当前区间中期(MCI)前、在当前区间结束前,以及超出当前区间等。紧急任务将获得更高的评分,普通任务则评分较低。公式(3)表明,具有紧急性质的出行目的($\alpha_{tp} > \omega$),例如应急响应和社会服务,只能选择前两个选项之一(ASAP 和 MCI)。在公式(3)中,$n$ 表示出发时间可用选项的总数,$k$ 表示紧急任务无法选择的最不重要选项的数量。类似地,较不重要的出行目的($\alpha_{tp} < \psi$),如休闲活动和居家购物,不能选择前几个选项。在公式(3)中,$m$ 表示最不重要任务无法选择的选项数量。该因素也可用于确定社会福利和社区福祉。
$$
\begin{cases}
\alpha_{tp} > \omega \rightarrow \alpha_{dt} \in rand(0, n-k) \
\alpha_{tp} < \psi \rightarrow \alpha_{dt} \in rand(n-m, n)
\end{cases} \quad (3)
$$ -
用户行为 :指电动汽车车主在遵守与充电站管理系统达成的协议方面的行为表现。例如,报告出行目的和电动汽车乘员类型的诚实程度可以被量化。有欺诈行为记录的电动汽车车主将通过扣减该项指标值受到惩罚,进而降低其未来获得优先级的机会。类似地,如果某辆电动汽车参与了需求响应或削峰填谷计划,则其违反或遵守协议的次数可作为衡量其行为的依据。同样,注册了这些计划的电动汽车相比未注册的电动汽车将获得正向奖励。该因素仅用于计算个体满意度。
C. 所需能量建模
所需能量的量 $E_{req}$ 电动汽车前往目的地($D_{dst}$)所需的能量是一个随机变量,它是到目的地的距离和电动汽车剩余电量($E_{res}$)的函数。电动汽车的剩余电量可通过公式(4)计算,其中 $E_{fin}$ 是电动汽车在一天开始时的最终能量值。$\mu_v$ 和 $\sigma_v$ 分别表示电动汽车行驶距离的均值和标准差。$E_{pkm}$ 表示电动汽车每公里能耗,$E_{cap}$ 表示电动汽车电池的容量。在紧急情况下,建议保留能量以用于后续的关键任务。此外,由于灾害仅影响特定区域,附近的部分充电站可能仍处于正常运行状态。因此,如果到附近正常运行充电站($D_{nst}$)的距离小于非紧急任务的实际目的地距离($D_{dst}$),则可将到目的地的距离($D_{dst}$)替换为到最近正常运行充电站的距离,如公式(5)所示。到达目标位置所需能量($E_{tar}$)可根据最终距离($D_{dst}$)的信息通过公式(6)计算。最后,每个电动汽车所需的能量量可根据剩余电量和目标能量信息通过公式(7)计算得出。
$$
E_{res} = E_{fin} - random(\mu_v, \sigma_v) / E_{pkm} * E_{cap} \quad (4)
$$
$$
(\alpha_{tp} < \psi) \& (D_{nst} < D_{dst}) \rightarrow D_{dst} = D_{nst} \quad (5)
$$
$$
E_{tar} = D_{dst} / E_{pkm} * E_{cap} \quad (6)
$$
$$
\begin{cases}
E_{tar} > E_{res} \rightarrow E_{req} = E_{tar} - E_{res} \
E_{tar} \leq E_{res} \rightarrow E_{req} = 0
\end{cases} \quad (7)
$$
D. 电力分配建议指标
为了分配可用能量,在考虑申领者时,仅个体满意度并不是一个充分的参数。不同车主的个体满意度可能相同,但他们在使用率上可能存在差异,即对社会和社区层面的影响[30]。因此,在本研究中,提出了三个指标,通过考虑电动汽车的社会、社区和个人影响来对其进行优先级排序。社会福利将被赋予最高优先级,其次是社区福祉,个体满意度将被赋予最低优先级。五种因素的不同组合,如前一节所述,这些计算用于得出将在以下各节中讨论的三个指标。
-
社会福利指数 :社会福利指数($I_{sw}$)表示将电力分配给特定电动汽车所带来的社会福利。社会福利指数是三个因素的函数,即出行目的、SOC差距和出发时间,如公式(8)所示。出行目的是决定电动汽车在社会福利方面优先级的主要因素。如果出行目的低于某一特定阈值($\omega$),则向该电动汽车分配电力不会带来社会福利,例如居家购物或休闲活动。通过定义一个二元变量($B_{sw}$)来表示社会福利,从而实现该目标,如公式(9)所示。如果两辆电动汽车具有相同的出行目的,则SOC差距较小的电动汽车将获得更高的优先级。引入出发时间的目标是使社会福利指数相较于其他两个指标具有更高的取值。
$$
I_{sw} = (\alpha_{tp} + \alpha_{sg} + \alpha_{dt}) \cdot B_{sw} \quad (8)
$$$$
\alpha_{tp} < \omega \rightarrow B_{sw} = 0 \quad ; \quad \alpha_{tp} \geq \omega \rightarrow B_{sw} = 1 \quad (9)
$$ -
社区福祉指数 :社区福祉指数($I_{cw}$)表示通过向特定电动汽车分配电力所实现的社区个体的福祉水平。该指数根据出行目的、电动汽车乘员、SOC差距和出发时间的信息计算得出,如公式(10)所示。出行目的和电动汽车乘员是决定社区福祉指数的两个主要因素。已使用一个二元变量($B_{cw}$)来过滤掉无社区福祉的电动汽车,即进行休闲活动的车辆,如公式(11)所示。对于出行目的和电动汽车乘员因素相同的电动汽车,SOC差距将决定更高优先级的车辆。最后,出发时间相较于个体满意度会将指数值向上调整。
$$
I_{cw} = (\alpha_{tp} + \alpha_{eo} + \alpha_{sg} + \alpha_{dt}) \cdot B_{cw} \quad (10)
$$$$
\alpha_{tp} < \psi \rightarrow B_{cw} = 0 \quad ; \quad \alpha_{tp} \geq \psi \rightarrow B_{cw} = 1 \quad (11)
$$ -
个体满意度指数 :它表示通过向特定电动汽车分配功率所能获得的个体满意程度。该指数仅是SOC差距和用户行为的函数,如公式(12)所示。与前两个指标不同,此指标对所有电动汽车均具有非零值。SOC差距优先考虑需要较少能量的电动汽车,这有助于利用可用功率为更多的电动汽车充电,从而提高更多客户的满意度。用户行为则激励那些没有欺诈行为记录、注册并遵守电网/充电站支持计划的客户。
$$
I_{is} = \alpha_{sg} + \alpha_{cb} \quad (12)
$$
确定电动汽车优先级的个体因素和指标的整体过程如图2所示。首先,选择选项并为每个选项分配评分,出行目的、电动汽车乘员、出发时间和客户行为的选项,需考虑每个选项的重要性。K、L和P分别表示出行目的、电动汽车乘员和出发时间的最大可选数量。类似地,Q表示客户行为的最大值,可以是其他因素范围内的任意有限数值。这四个数组均按降序排列,并为每辆电动汽车从每个数组中选择一个参数。根据出行目的,对电动汽车乘员和出发时间存在某些限制,例如残疾人不能选择应急响应,休闲活动的出发时间不可选择越快越好等。这些因素被分析,并在必要时使用(1)和(3)更新电动汽车乘员或出发时间的选项。在通过(4)‐(7)确定每辆电动汽车的所需能量后,计算SOC因子。在计算完全部五个因素后,分别使用(8)、(10)和(12)计算所提出的三个指标。社会福利和社区福祉受出行目的影响,例如,进行休闲活动没有社会福利,购物出行没有社区福祉。因此,将分析这些因素,并在需要时更新社会福利和社区福祉指标。然而,所有类型的出行目的都存在个体满意度,因此该指标无需更新。

III. 问题建模与求解方法
A. 多目标优化与帕累托最优性
理想情况下,多目标优化的目标是同时优化所有目标。然而,通常不存在对所有目标都最优的单一解,因此引入了帕累托最优的概念。如果不存在其他能够改进至少一个目标而不使其他目标恶化的解,则该解被称为帕累托最优。通常通过函数聚合来实现帕累托最优,但在聚合过程中也需要考虑公平性[31]。文献[32],[33]表明,公平的聚合应遵循单调性、公正性和均衡性原则。这些三项原则在电动汽车功率分配问题中的描述如下。
- 单调性 :当可用能量增加时,分配给每辆电动汽车的功率不应变得更差。
- 公正性 :分配给电动汽车的功率应基于可用功率的数量和需求的性质(出行目的、SOC差距等),而不是基于电动汽车所有者身份。
- 公平性 :分配功率以满足合理转移,从而最大化整体结果(社会福利、社区福祉以及个体满意度)。
加权和法是多目标优化中用于聚合函数的最常用方法。然而,该方法缺乏公正性和公平性[15]。此外,当输入数据或系统配置发生变化时,权重需要重新调整[25],并且无法获得帕累托前沿的凹部分[34]。加权和法的另一个主要缺点是无法生成均匀分布的帕累托点,因而可能无法准确表示帕累托前沿[35]。文献中提出了正态边界交点法(NBI方法)作为求解多目标优化问题中均匀分布帕累托最优解的替代方案[35]‐[37]。为了生成均匀分布的点,NBI采用了一种标量化方案,并且不受不同目标函数之间相对尺度的影响[36],而加权和法则不具备这一特性。然而,NBI的核心思想是获取边界点。因此,使用NBI得到的点可能并非帕累托最优解,因为帕累托最优解只是边界点的一个子集[35]。因此,NBI的主要缺点是无法保证所选点[35]的帕累托最优性。此外,文献[36]已证明,使用NBI的计算量随着变量数量、约束数量以及生成的帕累托点数量的增加而更快地增长。在[38]中,将NBI与epsilon(ɛ)‐约束法在求解不同问题时的性能进行了比较,并得出了以下结论:1)即使对于小规模问题,NBI的计算成本也很高。2). 随着问题复杂性的增加,分布质量下降。
因此,文献中提出了epsilon(ɛ)‐约束法作为克服前几段所述限制的潜在解决方案[39],[40]。在该方法中,其中一个目标函数(通常是最重要的目标)被求解,而其余目标函数则通过限制为用户定义值作为约束条件。该方法的优点是可以达到凹形部分,并且对权重因子不敏感。然而,该方法仅在处理两个目标函数时表现良好,当目标函数增多时复杂性增加[40]。此外,结果会随着目标函数的变化而变化,当存在两个或多个重要性相似的目标时,问题更加突出。
因此,字典序方法已被提出作为应对[15],[34],[41]中这些问题的潜在解决方案。已在[15]中证明,该方法满足所有公平性原则,且无需更新权重。相反,为每个目标函数定义优先级,只要相对优先级不变,解就保持不变。与无法保证解的帕累托最优性的NBI方法相比,使用字典序方法得到的解始终是帕累托最优的[34]。此外,已证明NBI的复杂性更高,因而比ɛ‐约束法计算成本更高[38],[42],而ɛ‐约束法的复杂性又高于字典序方法。与ɛ‐约束法相比,字典序方法确定的帕累托集更高效且非支配,最终获得的结果也更高效[40]。尽管可以通过增广以及在目标函数中定义松弛变量来提高ɛ‐约束法的性能[39]。然而,这些附加项会增加问题的复杂性,因此在计算上并不高效。因此,在本研究中,电动汽车的多目标功率分配问题通过字典序方法进行建模和求解。
B. 问题建模
该问题的目标是最大化总福利。总福利包括社会福利、社区福祉以及个体满意度,分别由公式(13)‐(15)给出。在这些方程中,$B_v$是一个二元变量,当分配给电动汽车vth 的能量($E_{all}$)大于或等于所需能量($E_{req}$)时,其值为1,否则为0,如公式(16)所示。$E_{all}$和$B_v$是所有三个目标函数的决策变量,其中$B_v$决定分配功率的电动汽车,$E_{all}$决定分配给每辆电动汽车的能量量。根据分配给每辆电动汽车的能量量,可通过公式(17)计算未满足能量($E_{us}$)。$I_{sw}$、$I_{cw}$和$I_{is}$分别表示社会福利、社区福祉和个体满意度的指标,这些指标在前一节中已作解释。在这些方程中,V表示电动汽车总数。
$$
f_1 = \max \sum_{v \in V} (B_v \cdot I_{sw} - E_{us} \cdot I_{sw}) \quad (13)
$$
$$
f_2 = \max \sum_{v \in V} (B_v \cdot I_{cw} - E_{us} \cdot I_{cw}) \quad (14)
$$
$$
f_3 = \max \sum_{v \in V} (B_v \cdot I_{is} - E_{us} \cdot I_{is}) \quad (15)
$$
约束条件:
$$
(E_{all} \geq E_{req}) \rightarrow B_v = 1 \quad ; \quad (E_{all} < E_{req}) \rightarrow B_v = 0 \quad (16)
$$
$$
E_{us} = E_{req} - E_{all} \quad (17)
$$
$$
\sum_{v \in V} E_{all} \leq E_{avl} \quad (18)
$$
(13)‐(15)中的第一部分表示满足特定电动汽车能源需求的激励,而第二部分表示未满足能源需求的惩罚。这些目标的约束由(16)‐(18)给出。方程(16)表示,对于任何电动汽车,只有当分配给该电动汽车的能量高于其所需能量时,才能获得每个目标中的激励(第一项)。方程(17)表示,任何电动汽车的未供应能量量可以通过该电动汽车所需的能量量和分配给该电动汽车的能量量来计算。最后,(18)约束了在该时间间隔内分配给所有电动汽车的总功率不得超过可用功率。
C. 基于字典序方法的求解方案
为了使用字典序方法求解所提出的问题,字典序方法除了需要其他输入数据外,还需要定义每个目标函数的优先级。使用字典序方法求解所建立的电动汽车功率分配问题的流程图如图3所示。在定义优先级后,首先选择具有最高优先级的目标函数,并在考虑所有约束的情况下将其作为单目标优化问题进行求解。第i个优先级的目标函数通式如(19)所示,其中S表示可行域。然后选择第二个目标函数,并通过定义附加约束(如(20)所示)将其作为单目标函数求解。该过程依次重复,将前一步骤的最优解作为新的约束加入。此处,i表示函数优先级序列,$f_j^*$表示第j个目标函数在第j轮中的最优值。当获得所有目标函数的唯一最优解或所有函数均已求解时,算法终止。使用字典序方法得到的解始终是帕累托最优[34]。
$$
\max f_i(B) \quad (19)
$$
约束条件:
$$
f_j(B) \leq f_j^*, \quad j=1, i-1; \quad i=1,I \quad (20)
$$
Equations(16)-(18)

D. 其他多目标优化求解方法与评价指标
本节将介绍这两种方法的概述,因为下一节将把字典序方法的性能与两种最常用的多目标优化求解方法(即加权和法和ɛ‐约束法)进行比较。
在加权和法的情况下,所有函数被加总为一个单一的目标函数,如(21)所示。为每个目标函数定义权重($w_i$),以表示不同目标的重要性。然后在所有目标函数的约束条件下求解该单一目标。
$$
\max \sum_{i=1}^{I} w_i \cdot f_i(B) \quad (21)
$$
Subject to: Equations(16)-(18)
在采用ɛ‐约束法的情况下,其中一个目标函数被求解,而其他目标函数则作为约束条件,如式(22)和(23)所示。为了应用ɛ‐约束法,需要至少I‐1个目标的取值范围,这些范围通常通过支付表[42]计算得到,如式(24)所示。为了构建支付表,首先计算各个目标的最优值(对角线元素)。然后,根据各个目标函数的最优值,计算其他目标函数的值(非对角线元素)。
为了分析所提出的方法在向电动汽车分配电力方面的性能,本文提出了两个指标。第一个指标(服务百分比指数)表示特定类别中已服务车辆的百分比。例如,社会福利类别电动汽车的服务百分比指数由公式(25)给出,其中$I_{sp_sw}$表示充电站内所有电动汽车的总社会福利。对于社区福利类别,仅使用社会福利为零的电动汽车;类似地,对于个体满意度类别,仅使用社会福利和社区福祉均为零的电动汽车。同样,社会福利类别电动汽车的第二个指标(未供应百分比指数)可通过公式(26)计算,其中$E_{up_sw}$表示每辆电动汽车所需能量与其SW指数乘积之和。这些指标也可用于其他类别,如社区福祉和个体满意度。
$$
f_1(B) = \max \quad (22)
$$
Subject to: Equations(16)-(18)
$$
f_i(B) \geq \epsilon_i, \quad i=2,I \quad (23)
$$
$$
\phi = \begin{bmatrix}
f_1^
(B_1^
) & f_1(B_2^
) & \cdots & f_1(B_I^
) \
f_2(B_1^
) & f_2^
(B_2^
) & \cdots & f_2(B_I^
) \
\vdots & \vdots & \ddots & \vdots \
f_I(B_1^
) & f_I(B_2^
) & \cdots & f_I^
(B_I^
)
\end{bmatrix} \quad (24)
$$
$$
I_{sp_sw} = 100 \cdot \frac{\sum_{v \in V} B_v \cdot I_{sw}}{I_{tot_sw}} \quad (25)
$$
$$
I_{up_sw} = 100 \cdot \frac{\sum_{v \in V} E_{us} \cdot I_{sw}}{E_{tot_req}} \quad (26)
$$
IV. 仿真结果:加权和法与所提出的字典序方法的比较
A. 输入数据
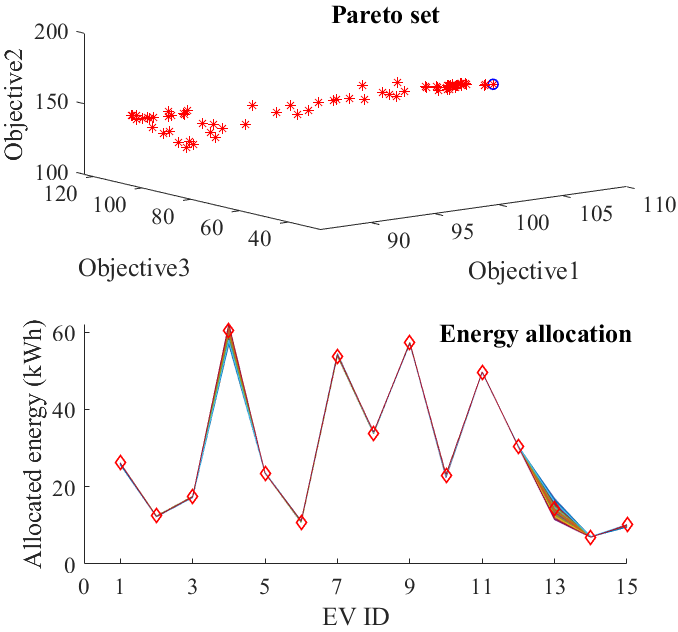
本节考虑了15辆电动汽车,以比较所提出的字典序方法与ε‐约束法和加权和法的性能。本研究中考虑的五个优先级因素为出行目的(TP)、电动汽车乘员(EO)、出发时间(DT)、用户行为(CB)和SOC差距(SG)。表 I列出了TP、EO和DT的离散选项及其对应值。TP和EO的选项取自全国家庭出行调查数据库[43],并在TP中添加了一些选项,以涵盖用于其他用途(如应急响应)的电动汽车。所有因素均按1到10的量表赋值,数值越高表示该类别越重要,反之亦然。CB在1到10之间随机生成,数值越高表示违规越少,反之亦然。最后,SG和所需能量分别通过公式(2)和(7)计算得出。EV的电池容量、续航里程和效率数据来自[44],用于计算所需能量。车辆每日行驶模式的数据取自[43],假设电动汽车也将遵循类似的行驶模式。社会福利(SW)、社区福祉(CW)和个体满意度(IS)的相应指标分别通过公式(8)、(10)和(12)计算得出。15辆电动汽车的因素信息、所需能量及各项指标列于表II中。任意时刻的可用能量数量通过使用可再生能源的预测值、电池的荷电状态以及微型涡轮机的容量,可以获得时间间隔。在本节中,考虑了可再生能源和荷电状态误差的最坏情况。下一节将分析这些误差对所提出的方法性能的影响。
为了可视化测试案例的帕累托前沿,采用了与表II中相同的输入数据,并将可用能量设为430千瓦时,这与下一节第(IV‐B)节中的案例1相同。帕累托集是通过使用 Matlab函数‘paretosearch’生成的,该函数用于寻找多目标函数的非支配点。通过此函数获得的帕累托集以及分配给不同电动汽车的相应功率值如图4所示。蓝色圆圈标记的点是由字典序方法选择的帕累托点,能量分配图中的菱形标记点是相应的分配的能量值。可以看出,字典序方法选择了目标1取值最高的点,这是由于目标1相较于其他两个目标(目标2和目标3)具有更高重要性。不同帕累托点之间分配功率的差异主要体现在电动汽车4和电动汽车13上,因此不同的方法将选择不同的帕累托点。结果的详细信息将在后续章节中讨论。
表I:因素的离散选项及对应值。
| 因素 | 离散选项和对应值 |
|---|---|
| TP | 应急响应 (10),社会服务 (8),访问医院 (6),工作/学习 (4),居家购物 (2),休闲活动 (1) |
| EO | 残疾人 (10),老年人 (8),携带儿童 (6),正常成年人 (1) |
| DT | 尽快 (10),在时间段中期之前 (4),在时间段结束前 (2),超出当前时间段 (1) |
表II:输入数据:优先级因素、所需能量和指标。
| 编号 | 出行目的 | 电动汽车乘员 | 出发时间 | 用户行为 | SG | RE | SW | CW | IS |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 1 | 4 | 2 | 5.4 | 26.2 | 17.4 | 18.4 | 7.4 |
| 2 | 10 | 1 | 10 | 10 | 8.7 | 12.5 | 28.7 | 29.7 | 18.7 |
| 3 | 8 | 1 | 4 | 10 | 8.2 | 17.6 | 20.2 | 21.2 | 18.2 |
| 4c1 | 4 | 1 | 2 | 1 | 0.7 | 62.6 | 0 | 7.7 | 1.7 |
| 5c2 | 4 | 8 | 2 | 5 | 7.6 | 23.8 | 0 | 21.6 | 12.6 |
| 6 | 2 | 8 | 2 | 9 | 8.9 | 11.4 | 0 | 0 | 17.9 |
| 7c1 | 4 | 1 | 1 | 3 | 0.5 | 54.8 | 0 | 6.5 | 3.5 |
| 8 | 6 | 10 | 2 | 1 | 6.6 | 34.2 | 0 | 24.6 | 7.6 |
| 9c2 | 8 | 1 | 4 | 2 | 1.2 | 57.6 | 13.2 | 14.2 | 3.2 |
| 10c2 | 4 | 8 | 10 | 7 | 7.6 | 23.5 | 0 | 29.6 | 14.6 |
| 11 | 8 | 1 | 10 | 6 | 5.0 | 49.9 | 23 | 24 | 11 |
| 12 | 10 | 1 | 4 | 7 | 6.9 | 30.6 | 20.9 | 21.9 | 13.9 |
| 13c1 | 1 | 6 | 2 | 9 | 8.3 | 17.2 | 0 | 0 | 17.3 |
| 14c2 | 6 | 8 | 4 | 9 | 9.3 | 7.1 | 0 | 27.3 | 18.3 |
| 15c2 | 1 | 1 | 4 | 10 | 8.9 | 10.5 | 0 | 0 | 18.9 |
B. 具有不同的重要性的目标
为了比较所提出的求解方法与常用多目标优化的性能,求解方法(ε‐约束和加权和法)在本节中考虑了两种情况,各目标的重要性在两种情况下有所不同。表II中蓝色(上标标记为c1)和橙色(上标标记为c2)的行分别对应案例 1和案例2。表III显示了不同方法在所有三种情况下服务的电动汽车数量。具有非零社会福利、社区福祉以及个体满意度值的电动汽车总数分别为6、12和15(所有情况相同)。各案例的详细信息如下。
-
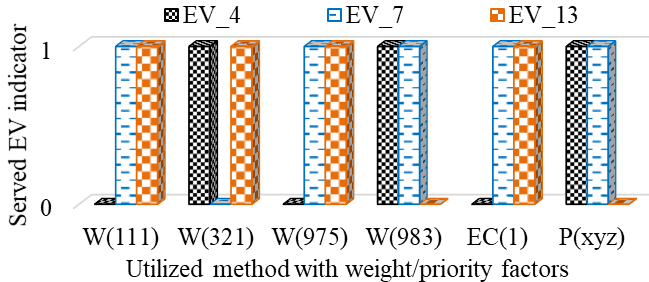
正常短缺情况(案例1) :在案例1中,可用能量(430千瓦时)几乎等于电动汽车车队所需的能量( 439.5千瓦时),即只有一到两辆电动汽车无法获得所需能量。由于加权和法对权重值较为敏感,因此通过改变公式(21)中的权重w考虑了四种情况。加权和法括号内的数值表示各目标函数的权重。例如,W (321) 表示目标1、2和3的权重分别为3、2和1。类似地,ε‐约束(EC)法中的数值表示被设为目标函数的目标,其余目标则作为约束条件。在15辆电动汽车中,仅在图5中显示了不同情况下服务指标不同的电动汽车。其余电动汽车的需求均被所有算法满足,因此不再进一步讨论。
从图5可以看出,随着权重值的变化,加权和法选择了不同的电动汽车,即优化结果在改变。而对于所提出的方法,只要满足优先级条件(x > y > z),无论优先级(xyz)取何值,结果都相同。从表IV可以看出,由于社区福祉具有较高优先级,所提出的方法中社区福祉的服务百分比指数为100%,个体满意度为68.02%。然而,在W(111)、W(321)和 W(975)的情况下,个体满意度的服务百分比指数为100%。且社区福祉为93.44%,这并不理想。类似地,在使用ɛ‐约束法的情况下,个体满意度为100%,而社区福祉为93.44%,与加权和法的前三种情况相同。这表明,所提出的方法通过将功率分配最大化给具有较高社区福祉值的电动汽车,表现更优;而加权和法与ɛ‐约束法则以牺牲社区福祉为代价,将功率分配给电动汽车以最大化个体满意度。
-
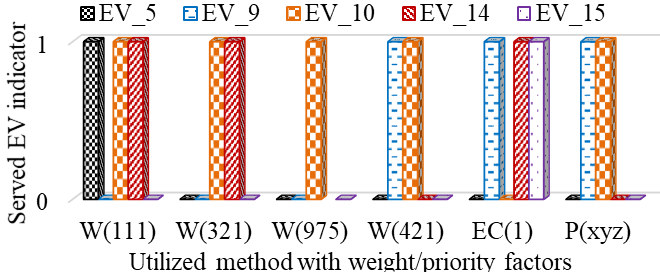
严重短缺情况(案例2) :在此情况下,可用能量( 220千瓦时)约为所需能量(439.5千瓦时)的50%。在此情况下,所提出的方法的性能也与加权和法的4种情况进行了比较。以及一种ɛ‐约束法的情况。从图6可以看出,随着权重因子的变化,服务的电动汽车数量也随之变化,与之前情况相同。表IV的右半部分显示,在W(111)、W(321)和 W(975)的情况下,社区福祉提高是以牺牲社会福利为代价的,这是不可接受的。在此情况下,尽管ɛ‐约束法的社会福利与所提出的方法相同,但社区福祉的值较低,这是由于个体满意度增加所致,而这并不理想,即社区福祉应优先于个体满意度。然而,在所提出的方法(P(xyz))中,由于社会福利具有更高优先级,首先实现了社会福利的最大化,其次是社区福祉,这正是所期望的结果。这意味着在这种情况下,ɛ‐约束法的表现优于大多数加权和情况,但所提出的方法仍通过遵循社会福利、社区福祉和个体满意度的优先级顺序,在整体性能上优于这两种方法。
从图5和图6可以看出,在案例1中,W(983)以及在案例2中W(421)所得到的服务百分比指标和服务的电动汽车数量与所提出的方法相同。然而,这些权重需要针对每种情况单独确定,这本身又是一个优化问题。通常,这些权重是基于试错法来确定的,使得该过程更具挑战性。同样,在两种情况下,ɛ‐约束法的性能均未达到所提出方法的水平。这是因为在该方法中仅选择一个目标函数,而将其他所有目标设为约束条件,导致所有剩余目标的重要性在ɛ‐约束法中被视为相同,因而无法区分这些剩余目标之间的相对重要性。而所提出的方法则能够在xyz值之间关系有效(即x > y > z)的前提下,无论xyz的具体取值如何,均能获得一致的结果,并且能够兼顾所有目标之间的相对重要性。
表III:不同案例和方法下服务的电动汽车数量。
| Case 方法 | 案例1 | 案例1 | 案例1 | 案例1 | 案例1 | 案例1 | 案例2 | 案例2 | 案例2 | 案例2 | 案例2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SW | SW | CW | CW | IS | IS | SW | SW | CW | CW | IS | |
| W(111) | 6 | 6 | 11 | 11 | 14 | 14 | 5 | 5 | 3 | 3 | 8 |
| W(321) | 6 | 6 | 11 | 11 | 14 | 14 | 5 | 5 | 2 | 2 | 7 |
| W(975) | 6 | 6 | 11 | 11 | 4 | 4 | 5 | 5 | 2 | 2 | 7 |
| W(983) | 6 | 6 | 12 | 12 | 14 | 14 | - | - | - | - | - |
| W(421) | - | - | - | - | - | - | 6 | 6 | 1 | 1 | 7 |
| EC(1) | 6 | 6 | 11 | 11 | 14 | 14 | 6 | 6 | 1 | 1 | 8 |
| P(xyz) | 6 | 6 | 12 | 12 | 14 | 14 | 6 | 6 | 1 | 1 | 7 |
表IV:不同情况下服务百分比指数的值(%)。
| SW方法 社区福祉 | SW方法 社区福祉 | SW方法 社区福祉 | SW方法 社区福祉 | SW方法 社区福祉 | SW方法 社区福祉 | case | case | case | case | case | case | case | case | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| W(111) 1 | 00 93. | 4 100 | 4 100 | IS | IS | SW方法 W(111) 8 | SW方法 W(111) 8 | 9.3 66. | 9.3 66. | CW 9 0.00 | CW 9 0.00 | IS | IS | |
| W(321) 1 | 00 94. | 5 100 | 5 100 | W(321) 8 | W(321) 8 | 9.3 48 | 9.3 48 | .5 0.00 | .5 0.00 | |||||
| W(975) 1 | 00 93. | 4 100 | 4 100 | W(975) 8 | W(975) 8 | 9.3 48 | 9.3 48 | .5 0.00 | .5 0.00 | |||||
| W(983) 1 | 00 100 | 68.1 | 68.1 | 100 2 | 100 2 | 5.2 0.0 | 5.2 0.0 | |||||||
| 100 9 | 3.4 10 | 3.4 10 | W(421) | W(421) | 100 2 | 100 2 | 3.3 34. | 3.3 34. | ||||||
| EC(1) | 100 1 | 00 68. | 00 68. | EC(1) | EC(1) | 100 2 | 100 2 | 5.2 0.0 | 5.2 0.0 | |||||
| P(xyz) | P(xyz) | P(xyz) |
C. 具有相似重要性的目标
在本节中,考虑了两种情况,通过设定两个目标的相对重要性相似,来评估所提出的字典序方法相较于ε‐约束法和加权和法的性能。
-
案例a :在本案例中,社会福利和社区福祉的重要性被设置为相同,而个体满意度的重要性被设置为较低。本案例的可用能量和所需能量与上一节中案例2相同。由于EC方法的性能随着目标函数选择的变化而变化,因此本节考虑了两种EC方法的情况以及两种加权和法的情况。
从表V(左半部分)可以看出,加权和法在权重值变化时,对EV8和EV9的功率分配量也不同。类似地,当采用不同的目标函数时,ε‐约束法也会改变对EV1、EV5、EV8‐EV10以及EV15的功率分配。这表明加权和法对权重值具有敏感性,而ε‐约束法对目标函数的选择具有敏感性。对于所提出的方法而言,无论选择何种优先级值(x>y),输出结果均保持不变。
由于在此案例中社会福利和社区福祉的意义相同,因此为两者计算一个指标,并为每种方法的个体满意度分别计算一个指标。从图7可以看出,在社会福利和社区福祉情况下(案例a),所提出的方法的未供应百分比指数最低。其他方法(加权和法和ε‐约束)虽然降低了个体满意度的未供应百分比指数,但却导致社会福利和社区福祉的未供应百分比指数升高。这是不可取的,因为个体满意度的重要性低于另外两个因素(社会福利和社区福祉)。
-
案例b :在本案例中,社区福祉与个体满意度的重要性被设为相同,而社会福利的重要性被设为更高。本案例的可用能量和所需能量与前一节的案例2相同。与前一节类似,本节考虑了两种情况的EC以及加权和法的两种情况。
表V的右半部分显示,对于ɛ‐约束法,分配给电动汽车(1、6、8、13和15)的功率随着目标函数的变化而变化。类似地,对于加权和法,分配给EV9和EV10的功率随着权重的变化而变化。然而,在满足条件x>y的情况下,所提出的方法无论优先级值如何,都会给出相同的结果。
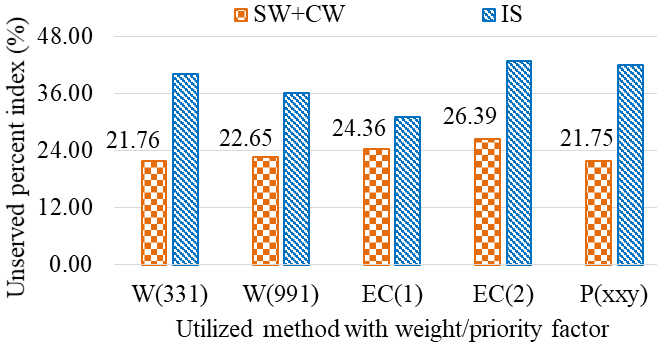
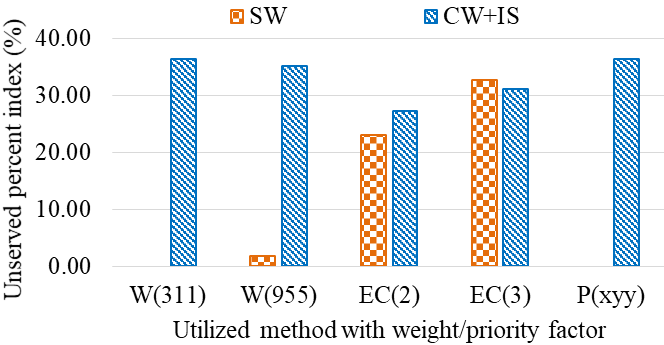
与之前的情况类似,社会福利计算一个指数,社区福祉和个体满意度则计算一个综合指数。从图8可以看出,在两种情况下,ε‐约束法的社会福利未供应百分比指数均高于所提出的方法,这是不理想的,因为在此情况下社会福利的重要性高于其他两个因素。加权和法的一种情况(W(311))得到的未供应百分比指数与所提出的方法相同,但这些权重的最优值需要确定。
表V:不同案例中的未满足能量量。
| 电动汽车编号 | 案例a | 案例a | 案例a | 案例a | 案例a | 案例b | 案例b | 案例b | 案例b | 案例b |
|---|---|---|---|---|---|---|---|---|---|---|
| W(331) | W(995) | EC(1) | EC(2) | P(xxy) | W(311) | W(955) | EC(2) | EC(3) | P(xyy) | |
| 1 | 0 | 0 | 5.4 | 0 | 0 | 0 | 0 | 5.4 | 26.18 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 62.6 | 62.6 | 62.6 | 54.67 | 62.6 | 62.6 | 62.6 | 62.6 | 62.6 | 62.6 |
| 5 | 23.8 | 23.8 | 0 | 23.8 | 23.8 | 23.8 | 23.8 | 0 | 0 | 23.8 |
| 6 | 11.4 | 11.4 | 11.4 | 11.4 | 11.4 | 11.4 | 11.4 | 11.4 | 0 | 11.4 |
| 7 | 54.8 | 54.8 | 54.8 | 54.8 | 54.8 | 54.8 | 54.8 | 54.8 | 54.8 | 54.8 |
| 8 | 34.2 | 0 | 0 | 34.14 | 34.2 | 34.2 | 34.2 | 0 | 18.32 | 34.2 |
| 9 | 5 | 39.2 | 57.6 | 0 | 0 | 0 | 5 | 57.6 | 57.6 | 0 |
| 10 | 0 | 0 | 0 | 23.5 | 0 | 5 | 0 | 0 | 0 | 5 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13 | 17.2 | 17.2 | 17.2 | 17.19 | 17.2 | 17.2 | 17.2 | 17.2 | 0 | 17.2 |
| 14 | 0 | 0 | 0 | 0 | 5.01 | 0 | 0 | 0 | 0 | 0 |
| 15 | 10.5 | 10.5 | 10.5 | 0 | 10.49 | 10.5 | 10.5 | 10.5 | 0 | 10.5 |
V. 讨论与分析
电动汽车优先级和功率分配的问题建模涉及多个不确定因素。因此,本节对这些不确定因素(电动汽车数量、可再生能源、SOC估计和所需能量)进行敏感性分析。在本节中,通过将每种情况下已服务/未服务的电动汽车数量与电动汽车总数进行比较,计算已服务和未服务的电动汽车数量。
A. 电动汽车渗透率
为了评估电动汽车数量的影响,本节考虑了五种情况(案例a、b、c、d、e),通过改变电动汽车数量,同时保持可用能量总量不变(430千瓦时)。每种情况下考虑的电动汽车总数分别为10、20、50、100和200,具有非零指标的电动汽车数量如表VI所示。在图9中,某一类别的服务的电动汽车值越高,表示该指标非零值的电动汽车被服务的数量越多,反之亦然。
从图9可以看出,随着电动汽车数量的增加,个体满意度(IS)的服务的电动汽车值下降,这是由于IS的优先级低于交换机(SW)和社区福祉(CW)。在最后三种情况(50、100和200)中,由于电力供应有限,交换机(SW)和社区福祉(CW)的服务的电动汽车值也有所下降。然而,由于交换机(SW)的优先级高于社区福祉(CW),其值始终高于社区福祉(CW)。这表明所提出的方法成功地优先将电力分配给具有最高交换机(SW)指标的电动汽车,其次是社区福祉(CW)和个体满意度(IS)指标。服务的电动汽车值减少的不规则趋势是由于每种情况下电动汽车所需能量的随机化所致。
表VI:具有非零对应指标的电动汽车数量。
| 参数 | 案例a | 案例b |




















 35
35

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








